P3266 [JLOI2015] 骗我呢

P3266 [JLOI2015] 骗我呢

考虑 dp。观察到每行只会有一个数字不会出现，所以设计状态 \(f_{i,j}\) 为第 \(i\) 行只有 \(j\) 这个数字没出现。

显然状态转移方程为

\[f_{i,j}=\sum_{k=0}^{j+1}f_{i-1,k} \]

上界为 \(j+1\) 的原因是当 \(k>j+1\) 时第 \(i\) 行的 \(j+1\) 所对的位置不满足 \(x_{i,j}<x_{i-1,j+1}\)。

观察上式可以发现 \(f_{i,j}\) 能由 \(f_{i,j-1}\) 推来，所以有

\[f_{i,j}=f_{i,j-1}+f_{i-1,j+1} \]

这样我们得到了 \(O(nm)\) 的 dp 了。

进一步想，先把每个点从何转移得来标注出来。

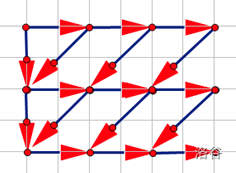
给它拉直

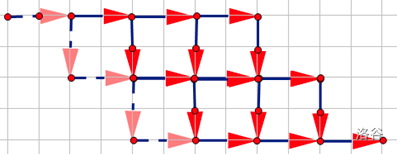
在对称一下

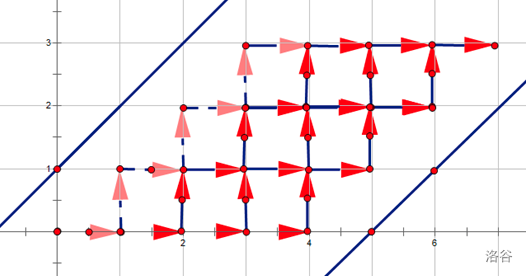
（图片来自转载，侵权即删）

发现了什么？我们要求的答案即为从 \((0,0)\) 到 \((n+m+1,n)\) 的路径且与 \(y=x+1\) 和 \(y=x-m-2\) 这两条线不相交的方案数。

\((0,0)\) 到 \((n+m+1,n)\) 的路径显然为 \({n+m+1\choose n}\)，考虑减去那些不合法的。

记 \(y=x+1\) 为 \(A\)，\(y=x-m-2\) 为 \(B\)。

那么我们如果每次经过一条线就写下来对应字母，缩起来相同的字母可以得到一个跨越直线的序列。

像比如：

• \(A\)

• \(B\)

• \(AB\)

• \(BA\)

• \(ABA\)

• \(BAB\)

• \(ABAB\)

• \(BABA\)

• \(\dots\)

答案为总数减去以 A 开头的路径个数再减去以 B 开头的路径总数。

以求以 \(A\) 开头的路径个数为例，现将终点作关于 \(A\) 对称，记为 \(A'\)，先减去 \(O\) 到 \(A'\) 的路径个数，会减去以 \(A\) 或 \(AB\) 结尾的路径，但是会多减去类似 \(BAB\) 这种 \(B\) 开头的路径。那么我们再作 \(A'\) 关于 \(B\) 对称，记为 \(A''\)，加上 \(O\) 到 \(A''\) 的路径，前面多减的加回来了，但是又多加了类似 \(BABA\) 的路径，我们在加上……

怎么对称？有结论点 \((x,y)\) 关于直线 \(y=x+b\) 的对称点为 \((y-b,x+b)\)，套进去就行。

code:

#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;

inline int read() {
	int x = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
	while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
	return x*f;
}

inline void write(int x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x/10);
	putchar('0'+x%10);
}

const int N = 3e6+5, mod = 1e9+7;
int n, m, k, ans, fac[N], ifac[N];

int qpow(int x, int y) {
	int res = 1;
	for (; y; y >>= 1, x = 1ll*x*x%mod) if (y&1) res = 1ll*res*x%mod;
	return res;
}

int c(int x, int y) {
	if (x < 0 || y < 0 || x < y) return 0;
	return 1ll*fac[x]*ifac[y]%mod*ifac[x-y]%mod;
}

void init(int n) {
	fac[0] = 1;
	for (int i = 1; i <= n; ++i) fac[i] = 1ll*fac[i-1]*i%mod;
	ifac[n] = qpow(fac[n], mod-2);
	for (int i = n-1; ~i; --i) ifac[i] = 1ll*ifac[i+1]*(i+1)%mod;
}

void pls(int &x, int y) { x = (x+y)%mod; }

void sub(int &x, int y) { x = (x-y+mod)%mod; }

void flip1(int &x, int &y) { swap(x, y); --x, ++y; }

void flip2(int &x, int &y) { swap(x, y); x += m+2, y -= m+2; }

int main() {
	init(N-5);
	n = read(), m = read();
	int x = n+m+1, y = n;
	ans = c(x+y, x);
	while (x >= 0 && y >= 0) {
		flip1(x, y), sub(ans, c(x+y, x));
		flip2(x, y), pls(ans, c(x+y, x));
	}
	x = n+m+1, y = n;
	while (x >= 0 && y >= 0) {
		flip2(x, y), sub(ans, c(x+y, x));
		flip1(x, y), pls(ans, c(x+y, x));
	}
	write(ans);
	return 0;
}