图的连通性
前言
存个模板,以免忘记了。
无向图
定义
Tarjan 算法主要用到两个值,分别为时间戳 \(dfn_x\) 以及追溯值 \(low_x\),其中 \(low_x\) 的定义为点 \(x\) 的子树中的一点能通过一条返祖边所能到的点的最小时间戳。
这里给张图:
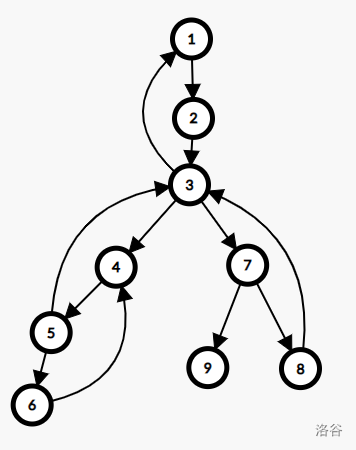
9 12
1 2
2 3
3 4
4 5
5 6
3 7
7 8
7 9
1 3
3 5
3 8
4 6
根据定义,为了计算 \(low_x\),应该先令 \(low_x = dfn_x\),然后考虑从 \(x\) 出发的每条边 \((x,y)\):
若在搜索树上 \(x\) 是 \(y\) 的父节点,则令 \(low_x=\min(low_x,low_y)\)。
若无向边 \((x,y)\) 不是搜索树上的边,则令 \(low_x=\min(low_x,dfn_y)\)。
下面的表格中标注了上图中每个节点的 \(low\)。
| \(i\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) |
|---|---|---|---|---|---|---|---|---|---|
| \(low_i\) | \(1\) | \(1\) | \(1\) | \(3\) | \(3\) | \(4\) | \(3\) | \(3\) | \(7\) |
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5;
int n, m, idx, dfn[N], low[N];
vector <int> E[N];
inline void tarjan(int x) {
dfn[x] = low[x] = ++idx;
for (int y:E[x]) {
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
}
else low[x] = min(low[x], dfn[y]);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
E[x].pb(y), E[y].pb(x);
}
tarjan(1);
for (int i = 1; i <= n; ++i) write(low[i]), space;
return 0;
}
割边
割边判定法则:无向边 \((x,y)\) 是桥,当且仅当搜索树上存在 \(x\) 的一个子节点 \(y\),满足:\(dfn_x<low_y\)。
例如上图中,\((7,9)\) 为桥。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, idx, cnt, tot = 1, dfn[N], low[N], head[N], bridge[M];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++idx;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y, i);
low[x] = min(low[x], low[y]);
if (low[y] > dfn[x]) bridge[i] = bridge[i^1] = 1;
}
else if (i != (in_edge^1)) low[x] = min(low[x], dfn[y]);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y), add(y, x);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i, 0);
for (int i = 2; i < tot; i += 2) if (bridge[i]) write(e[i^1].to), space, write(e[i].to), enter;
return 0;
}
割点
割点判定法则:若 \(x\) 不是搜索树的根节点(深度优先遍历的起点),则 \(x\) 是割点当且仅当搜索树上存在 \(x\) 的一个子节点 \(y\),满足:\(dfn_x\le low_y\)。特别地,若 \(x\) 是搜索树的根节点,则 \(x\) 是割点当且仅当搜索树上存在至少两个子节点 \(y1,y2\) 满足上述条件。
例如上图中,\(3,7\) 为割点。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, tot, idx, cnt, root, dfn[N], low[N], head[N];
bool cut[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x) {
int flag = 0; dfn[x] = low[x] = ++idx;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) {
++flag;
if (x != root || flag > 1) cut[x] = 1;
}
}
else low[x] = min(low[x], dfn[y]);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y), add(y, x);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) root = i, tarjan(i);
for (int i = 1; i <= n; ++i) if (cut[i]) ++cnt;
write(cnt), enter;
for (int i = 1; i <= n; ++i) if (cut[i]) write(i), space;
return 0;
}
边双联通分量(e-DCC)
边双连通分量的计算非常容易。只需求出无向图中所有的桥,把桥都删除后,无向图会分成若干个连通块,每一个连通块就是一个边双连通分量。
例如上图中,有 \(1\) 条割边 \((7,9)\),\(2\) 个 e-DCC,分别为 \(\{1,2,3,4,5,6,7,8\},\{9\}\)。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, idx, cnt, tot = 1, c[N], dfn[N], low[N], head[N], bridge[M];
vector <int> dcc[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++idx;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y, i);
low[x] = min(low[x], low[y]);
if (low[y] > dfn[x]) bridge[i] = bridge[i^1] = 1;
}
else if (i != (in_edge^1)) low[x] = min(low[x], dfn[y]);
}
}
inline void dfs(int x) {
c[x] = cnt;
dcc[cnt].pb(x);
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!c[y] && !bridge[i]) dfs(y);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y), add(y, x);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i, 0);
for (int i = 1; i <= n; ++i) if (!c[i]) ++cnt, dfs(i);
write(cnt), enter;
for (int i = 1; i <= cnt; ++i) {
write(dcc[i].size()), space;
for (int x:dcc[i]) write(x), space;
enter;
}
return 0;
}
e-DCC 的缩点
把每个 e-DCC 看作一个节点,把桥边 (x,y)看作连接编号为 \(c_x\) 和 \(c_y\) 的 e-DCC 对应节点的无向边,会产生一棵树(若原来的无向图不连通,则产生森林)。这种把e-DCC 收缩为一个节点的方法就称为缩点。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, idx, cnt, tot = 1, c[N], dfn[N], low[N], head[N], bridge[M];
vector <int> dcc[N], G[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++idx;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y, i);
low[x] = min(low[x], low[y]);
if (low[y] > dfn[x]) bridge[i] = bridge[i^1] = 1;
}
else if (i != (in_edge^1)) low[x] = min(low[x], dfn[y]);
}
}
inline void dfs(int x) {
c[x] = cnt;
dcc[cnt].pb(x);
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!c[y] && !bridge[i]) dfs(y);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y), add(y, x);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i, 0);
for (int i = 1; i <= n; ++i) if (!c[i]) ++cnt, dfs(i);
for (int i = 2; i <= tot; ++i) {
int x = e[i^1].to, y = e[i].to;
if (c[x] == c[y]) continue;
G[c[x]].pb(c[y]), G[c[y]].pb(c[x]);//G即为缩点后的树(或森林),点数cnt个
}
return 0;
}
点双联通分量(v-DCC)
若某个节点为孤立点,则它自己单独构成一个 v-DCC。除了孤立点之外,点双连通分量的大小至少为 \(2\)。根据 v-DCC 定义中的“极大”性,虽然桥不属于任何 e-DCC,但是割点可能属于多个 v-DCC。
为了求出点双连通分量,需要在 Tarjan 算法的过程中维护一个栈,并按照如下方法维护栈中的元素:
-
当一个节点第一次被访问时,把该节点入栈
-
当割点判定法则中的条件 \(dfn_x\le low_y\) 成立时,无论 \(x\) 是否为根,都要:
(1) 从栈顶不断弹出节点,直至节点 \(y\) 被弹出。
(2) 刚才弹出的所有节点与节点x起构成一个 v-DCC。
例如上图中,v-DCC 有 \(4\) 个,分别为 \(\{1,2,3\},\{3,4,5,6\},\{3,7,8\},\{7,9\}\)
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 5e5+5, M = 4e6+5;
struct edge { int to, next; } e[M];
int n, m, idx, cnt, top, tot, root, dfn[N], low[N], stk[N], cut[N], head[N];
vector <int> dcc[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x) {
int flag = 0; dfn[x] = low[x] = ++idx; stk[++top] = x;
if (x == root && !head[x]) return (void)(dcc[++cnt].pb(x));
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) {
++flag, ++cnt;
if (x != root || flag > 1) cut[x] = 1;
while (stk[top] != y) dcc[cnt].pb(stk[top--]);
--top, dcc[cnt].pb(x), dcc[cnt].pb(y);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
if (x == y) continue;
add(x, y), add(y, x);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) root = i, tarjan(i);
write(cnt), enter;
for (int i = 1; i <= cnt; ++i) {
write(dcc[i].size()), space;
for (int x:dcc[i]) write(x), space;
enter;
}
return 0;
}
v-DCC 的缩点
v-DCC 的缩点比 e-DCC 要复杂一些,因为一个割点可能属于多个 v-DCC。设图中共有 \(p\) 个割点和 \(t\) 个 v-DCC。我们建立一张包含 \(p+t\) 个节点的新图,把每个 v-DCC 和每个割点都作为新图中的节点,并在每个割点与包含它的所有 v-DCC 之间连边。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, idx, cnt, top, tot = 1, root, c[N], id[N], dfn[N], low[N], cut[N], stk[N], head[N];
vector <int> dcc[N], G[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x) {
int flag = 0; dfn[x] = low[x] = ++idx; stk[++top] = x;
if (x == root && !head[x]) return (void)(dcc[++cnt].pb(x));
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) {
++flag, ++cnt;
if (x != root || flag > 1) cut[x] = 1;
while (stk[top] != y) dcc[cnt].pb(stk[top--]);
--top, dcc[cnt].pb(x), dcc[cnt].pb(y);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
if (x == y) continue;
add(x, y), add(y, x);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) root = i, tarjan(i);
idx = cnt;
for (int i = 1; i <= n; ++i) if (cut[i]) id[i] = ++idx;
for (int i = 1; i <= cnt; ++i)
for (int x:dcc[i]) {
if (cut[x]) G[i].pb(id[x]), G[id[x]].pb(i);//G即为缩点后的树(或森林),点数idx个
else c[x] = i;
}
return 0;
}
有向图
定义
这里还是放张图(其中粗边为树边):
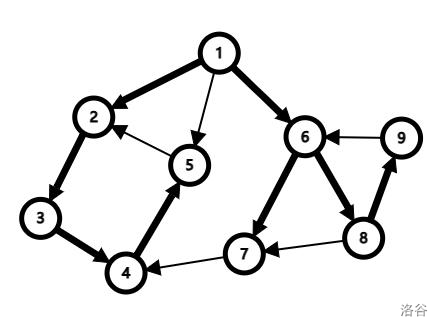
9 13
1 2
2 3
3 4
4 5
1 6
6 8
6 7
8 9
1 5
5 2
7 4
8 7
9 6
给定有向图 \(G=(V,E)\),若存在 \(r\in V\),满足从 \(r\) 出发能够到达 \(V\) 中所有的点,则称 \(G\) 是一个“流图”(Flow Graph),记为 \((G,r)\),其中 \(r\) 称为流图的源点。
流图中的每条有向边 \((x,y)\) 必然是以下四种之一:
-
树枝边,指搜索树中的边,即 \(x\) 是 \(y\) 的父节点。
-
前向边,指搜索树中 \(x\) 是 \(y\) 的祖先节点。
-
后向边,指搜索树中 \(y\) 是 \(x\) 的祖先节点。
-
横叉边,指除了以上三种情况之外的边,它一定满足 \(dfn_y<dfn_x\)。
强连通分量(SCC)
一个环一定是强连通图。如果既存在从 \(x\) 到 \(y\) 的路,也存在从 \(y\) 到 \(x\) 的路径,那么 \(x,y\) 显然在一个环中。因此,Tarjan 算法的基本思路就是对于每个点,尽量找到与它一起能构成环的所有节点。
容易发现,“前向边” \((x,y)\) 没有什么用处,因为搜索树上本来就存在从 \(x\) 到 \(y\) 的路径。“后向边” \((x,y)\) 非常有用,因为它可以和搜索树上从 \(y\) 到 \(x\) 的路径一起构成环。“横叉边”\((x,y)\)视情况而定,如果从 \(y\) 出发能找到一条路径回到 \(x\) 的祖先节点,那么 \((x,y)\) 就是有用的。
为了找到通过“后向边”和“横叉边”构成的环,Tarjan 算法在深度优先遍历的同时维护了一个栈。当访问到节点 \(x\) 时,栈中需要保存以下两类节点:
- 搜索树上 \(x\) 的祖先节点,记为集合 \(anc(x)\)。
设 \(y\in anc(x)\)。若存在后向边 \((x,y)\),则 \((x,y)\) 与 \(y\) 到 \(x\) 的路径一起形成环。
- 已经访问过,并且存在一条路径到达 \(anc(x)\) 的节点。
设 \(z\) 是一个这样的点,从 \(z\) 出发存在一条路径到达 \(y\in anc(x)\)。若存在横叉边 \((x,z)\),则 \((x,z)\)、\(z\) 到 \(y\) 的路径、\(y\) 到 \(x\) 的路径形成一个环。
综上所述,栈中的节点就是能与从 \(x\) 出发的“后向边”和“横叉边”形成环的节点。进而可以引入“追溯值”的概念。
追溯值
设 \(subtree(x)\) 表示流图的搜索树中以 \(x\) 为根的子树。\(x\) 的追溯值 \(low_x\) 定义为满足以下条件的节点的最小时间戳:
-
该点在栈中。
-
存在一条从 \(subtree(x)\) 出发的有向边,以该点为终点。
根据定义,Tarjan 算法按照以下步骤计算“追溯值”:
-
当节点 \(x\) 第一次被访问时,把 \(x\) 入栈,初始化 \(low_x=dfn_x\)。
-
扫描从 x出发的每条边 \((x,y)\)。
(1) 若 \(y\) 没被访问过,则说明 \((x,y)\) 是树枝边,递归访问 \(y\),从 \(y\) 回溯之后,令 \(low_x\) = \min(low_x,low_y)$
(2) 若 \(y\) 被访问过并且 \(y\) 在栈中,则令 \(low_x=\min(low_x,dfn_y)\)。
- 从 \(x\) 回溯之前,判断是否有 \(low_x=dfn_x\)。若成立,则不断从栈中弹出节点,直至 \(x\) 出栈。
下面表格中为上图各点的 \(low_x\) 值。
| \(i\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) |
|---|---|---|---|---|---|---|---|---|---|
| \(low_i\) | \(1\) | \(2\) | \(2\) | \(2\) | \(2\) | \(6\) | \(7\) | \(6\) | \(6\) |
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, tot, idx, top, dfn[N], low[N], stk[N], ins[N], head[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x) {
dfn[x] = low[x] = ++idx, stk[++top] = x, ins[x] = 1;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
}
else if (ins[y]) low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
while (stk[top] != x) ins[stk[top--]] = 0;
ins[stk[top--]] = 0;
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) write(low[i]), space;
return 0;
}
强连通分量判定法则
在追溯值的计算过程中,若从 \(x\) 回溯前,有 \(low_x=dfn_x\) 成立,则中从 \(x\) 到栈顶的所有节点构成一个强连通分量。
例如上图,SCC 有 \(4\) 个分别为 \(\{1\},\{7\},\{2,3,4,5\},\{6,8,9\}\)。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, tot, cnt, idx, top, c[N], dfn[N], low[N], stk[N], ins[N], head[N];
vector <int> scc[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x) {
dfn[x] = low[x] = ++idx, stk[++top] = x, ins[x] = 1;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
}
else if (ins[y]) low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
++cnt;
while (stk[top] != x) c[stk[top]] = cnt, scc[cnt].pb(stk[top]), ins[stk[top--]] = 0;
--top, c[x] = cnt, scc[cnt].pb(x), ins[x] = 0;
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
write(cnt), enter;
for (int i = 1, l; i <= cnt; ++i) {
write(scc[i].size()), space;
for (int x:scc[i]) write(x), space;
enter;
}
return 0;
}
SCC 的缩点
与无向图 e-DCC 的缩点类似,我们也可以把每个 SCC 缩成一个点。对原图中的每条有向边 \((x,y)\),若 \(c[x]\ne c[y]\),则在编号为 \(c[x]\) 与编号为 \(c[y]\) 的 SCC 之间连边。最后,我们会得到一张有向无环图。
code:
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
return x*f;
}
inline void write(int x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x/10);
putchar('0'+x%10);
}
const int N = 1e5+5, M = 2e5+5;
struct edge { int to, next; } e[M];
int n, m, tot, cnt, idx, top, c[N], dfn[N], low[N], stk[N], ins[N], head[N];
vector <int> scc[N], G[N];
inline void add(int x, int y) { e[++tot] = {y, head[x]}, head[x] = tot; }
inline void tarjan(int x) {
dfn[x] = low[x] = ++idx, stk[++top] = x, ins[x] = 1;
for (int i = head[x]; i; i = e[i].next)
if (!dfn[e[i].to]) {
tarjan(e[i].to);
low[x] = min(low[x], low[e[i].to]);
}
else if (ins[e[i].to]) low[x] = min(low[x], dfn[e[i].to]);
if (dfn[x] == low[x]) {
++cnt;
while (stk[top] != x) c[stk[top]] = cnt, scc[cnt].pb(stk[top]), ins[stk[top--]] = 0;
--top, c[x] = cnt, scc[cnt].pb(x), ins[x] = 0;
}
}
int main() {
n = read(), m = read();
while (m--) {
int x = read(), y = read();
add(x, y);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int x = 1; x <= n; ++x)
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (c[x] != c[y]) G[c[x]].pb(c[y]), G[c[y]].pb(c[x]);//G即为缩点后的树(或森林),点数cnt个
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号