线段树优化建图

最近在看线段树，于是随手写下了这一篇。

CF786B Legacy

---

题意简述

• \(q\) 次操作， \(3\) 种操作分别是建条 \(v\) 向 \(u\) 、\(\forall i\in [l,r]\) 向 \(v\) 、 \(v\) 向 \(\forall i\in [l,r]\) 权值为 \(w\) 的有向边

• 求起点为 \(s\) 的最短路

• \(1\le n,q\le 10^5\) ， \(1\le w \le 10^9\)

题目分析

暴力建图显然是不行的，就得用到线段树了。

线段树优化建图

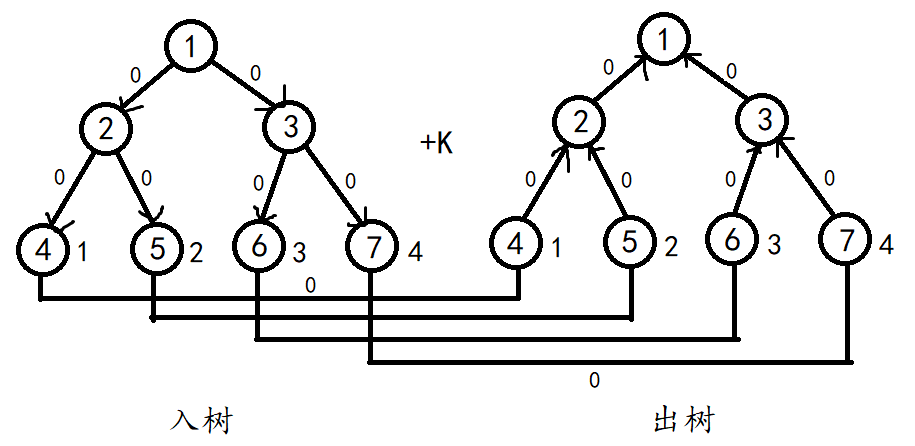
可以建两个线段树，分别是入树和出树，叶子节点则就是图的点。入树的父亲节点要指向左儿子和右儿子，权值为 \(0\) ；出树的左儿子和右儿子要指向父亲节点，权值为 \(0\) 。入树和出树对应的叶子节点建条边，权值也为 \(0\) 。

\(opt1\) ：将对应的 \(v\) 指向对应的 \(u\) 即可。

\(opt2\) ：若某个节点 \(p\) 被区间 \([l, r]\) 覆盖，就将节点 \(p\) 指向 \(v\) 。

\(opt3\) ：同理，将 \(v\) 指向节点 \(p\) 。

代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e6+5, M = N;
struct edge {
	int to, next; ll w;//万恶的long long
} e[M];
struct tree {
	int l, r;
} t[N<<1];
int n, q, s, k, op, tot, a[N], head[N];
ll dis[N];
bool vis[N];
void add(int x, int y, ll w) {
	e[++tot] = (edge){y, head[x], w};
	head[x] = tot;
}
void build(int p, int l, int r) {
	t[p].l = l, t[p].r = r;
	if (l == r) {//叶子节点
		a[l] = p;//记录编号
		return;
	}
	int mid = (l+r)>>1;
	add(p, p<<1, 0), add(p, p<<1|1, 0);//入树
	add((p<<1)+k, p+k, 0), add((p<<1|1)+k, p+k, 0);//出树
	build(p<<1, l, mid);
	build(p<<1|1, mid+1, r);
}
void change(int p, int l, int r, int v, ll w) {
	if (l <= t[p].l && t[p].r <= r) {//被覆盖
		if (op == 2) add(v+k, p, w);//出树指向入树
		else add(p+k, v, w);
		return;
	}
	int mid = (t[p].l+t[p].r)>>1;
	if (l <= mid) change(p<<1, l, r, v, w);
	if (mid < r) change(p<<1|1, l, r, v, w);
}
void dijkstra(int s) {//最短路
	memset(dis, 0x3f, sizeof(dis)), dis[s] = 0;
	priority_queue < pair<ll, int> > q;
	q.push(make_pair(0, s));
	while (!q.empty()) {
		int x = q.top().second; q.pop();
		if (vis[x]) continue;
		vis[x] = true;
		for(int i = head[x]; i; i = e[i].next) {
			int y = e[i].to;
			ll w = e[i].w;
			if (dis[y] > dis[x]+w) {
				dis[y] = dis[x]+w;
				q.push(make_pair(-dis[y], y));
			}
		}
	}
}
int main() {
	cin >> n >> q >> s;
	k = n<<2;
	build(1, 1, n);
	for (int i = 1; i <= n; ++i) add(a[i], a[i]+k, 0), add(a[i]+k, a[i], 0);//初始化
	int x, v, u, l, r; ll w;
	while (q--) {
		cin >> op;
		if (op == 1) {
			cin >> v >> u >> w;
			add(a[v]+k, a[u], w);
		}
		else {
			cin >> x >> l >> r >> w;
			change(1, l, r, a[x], w);
		}
	}
	dijkstra(a[s]+k);//注意是从出树开始
	for (int i = 1; i <= n; ++i) {
		if (dis[a[i]] == 0x3f3f3f3f3f3f3f3fll) cout << -1 << ' ';//如果到达不了
		else cout << dis[a[i]] << ' ';
	}
	return 0;
}