树状数组
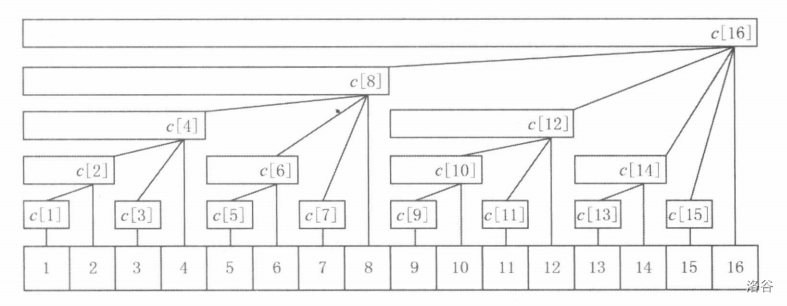
树状数组真的很精美,码量小,还很快,比线段树快多了[滑稽]。
一维树状数组
单点修改,区间查询
loj #130. 树状数组 1
lougu P3374【模板】树状数组 1
不多说,代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n, m, c[N];
int lowbit(int k) {return k&-k;}
void add(int x, int d) {for (; x <= n; x += lowbit(x)) c[x] += d;}
int ask(int x) {
int sum = 0;
for (; x; x -= lowbit(x)) sum += c[x];
return sum;
}
int main() {
ios::sync_with_stdio(0);
cin >> n >> m;
for (int i = 1, x; i <= n; ++i) {
cin >> x;
add(i, x);
}
for (int op, x, y; m--; ) {
cin >> op >> x >> y;
if (op == 1) add(x, y);
else cout << ask(y)-ask(x-1) << endl;
}
return 0;
}
区间修改,单点查询
loj #131. 树状数组 2
luogu P3368【模板】树状数组 2
不多说,代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n, m, a[N], c[N];
int lowbit(int k) {return k&-k;}
void add(int x, int d) {for (; x <= n; x += lowbit(x)) c[x] += d;}
int ask(int x) {
int sum = 0;
for (; x; x -= lowbit(x)) sum += c[x];
return sum;
}
int main() {
ios::sync_with_stdio(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int op, x, y, k; m--; ) {
cin >> op >> x;
if (op == 1) {
cin >> y >> k;
add(x, k);
add(y+1, -k);
}
else cout << a[x]+ask(x) << '\n';
}
return 0;
}
区间修改,区间查询
loj #132. 树状数组 3
定义数组 \(a[i]\) 为修改前的值,\(d[i]\) 为差分数组。
每次修改 \(a[x]\) 增加的值为:
\[\sum_{i=1}^{x}d[i]
\]
那么 \(a[1\dots x]\) 增加的值为:
\[\Delta sum=\sum_{i=1}^{x}\sum_{j=1}^{i}d[j]
\]
展开来方便看:
\[\Delta sum=(d[1])+(d[1]+d[2])+(d[1]+d[2]+d[3])+\dots+(d[1]+d[2]+\dots d[x])
\]
合并:
\[\Delta sum=d[1]\times x+d[2]\times(x-1)+\dots+d[x]\times 1
\]
化简下:
\[\Delta sum=(x+1)\times\sum_{i=1}^{x}d[i]-\sum_{i=1}^{x}d[i]*i
\]
不难发现,我们把 \(\Delta sum\) 拆成了维护 \(d[i]\) 和 \(d[i]\times i\) 的前缀。分别用树状数组 \(c1,c2\) 维护即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6+5;
int n, m, c1[N], c2[N], sum[N];
int lowbit(int k) {return k&-k;}
void add(int x, int d) {
for (int i = x; i <= n; i += lowbit(i)) {
c1[i] += d;
c2[i] += x*d;
}
}
int ask(int x) {
int sum = 0;
for (int i = x; i; i -= lowbit(i)) sum += (x+1)*c1[i]-c2[i];
return sum;
}
signed main() {
ios::sync_with_stdio(0);
cin >> n >> m;
for (int i = 1, x; i <= n; ++i) {
cin >> x;
sum[i] = sum[i-1]+x;
}
for (int opt, l, r, k; m--; ) {
cin >> opt >> l >> r;
if (opt == 1) {
cin >> k;
add(l, k);
add(r+1, -k);
}
else cout << sum[r]-sum[l-1]+ask(r)-ask(l-1) << '\n';
}
return 0;
}
二维树状数组
单点修改,区间查询
loj #133. 二维树状数组 1
不多说,代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e3;
int n, m, c[N][N];
int lowbit(int k) {return k&-k;}
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
c[i][j] += d;
}
int ask(int x, int y) {
int sum = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
sum += c[i][j];
return sum;
}
signed main() {
ios::sync_with_stdio(0);
cin >> n >> m;
int opt, x, y, k, x1, y1, x2, y2;
while (cin >> opt) {
if (opt == 1) {
cin >> x >> y >> k;
add(x, y, k);
}
else {
cin >> x1 >> y1 >> x2 >> y2;
cout << ask(x2, y2)-ask(x1-1, y2)-ask(x2, y1-1)+ask(x1-1, y1-1) << '\n';
}
}
return 0;
}
区间修改,单点查询
loj #134. 二维树状数组 2
不多说,代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e3;
int n, m, c[N][N];
int lowbit(int k) {return k&-k;}
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
c[i][j] += d;
}
int ask(int x, int y) {
int sum = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
sum += c[i][j];
return sum;
}
signed main() {
ios::sync_with_stdio(0);
cin >> n >> m;
int opt, x, y, x1, y1, x2, y2, k;
while (cin >> opt) {
if (opt == 1) {
cin >> x1 >> y1 >> x2 >> y2 >> k;
add(x1, y1, k);
add(x1, y2+1, -k);
add(x2+1, y1, -k);
add(x2+1, y2+1, k);
}
else {
cin >> x >> y;
cout << ask(x, y) << '\n';
}
}
return 0;
}
区间修改,区间查询
loj #135. 二维树状数组 3
luogu P4514 上帝造题的七分钟
显然一个矩阵的增加值为
\[\Delta sum=\sum_{x=1}^{i}\sum_{y=1}^{j}(\sum_{u=1}^{x}\sum_{v=1}^{y}d[u,v])
\]
我们仿造一维树状数组的操作,我们可以统计 \(d[u,v]\) 出现次数:
从 \(a[1,1]\) 到 \(a[i,j]\),\(d[1,1]\) 全部都要出现一次,所以有 \(i\times j\) 个 \(d[1,1]\),即 \(d[1,1]\times i\times j\)。类似的,有 \(d[1,2]\times i\times(j-1),d_{}[2,1]\times(i-1)\times j,d[2,2]\times(i-1)\times(j-1)\) 等等。
所以我们可以把式子变成:
\[\Delta sum=\sum_{x=1}^{i}\sum_{y=1}^{j}{\Large[}d[x,y]\times(i-x+1)\times(j-y+1){\Large]}
\]
展开得到:
\[\Delta sum=\sum_{x=1}^{i}\sum_{y=1}^{j}{\Large[}d[x,y]\times(i+1)(j+1)-d[x,y]\times x(j+1)-d[x,y]\times (i+1)y+d[x,y]\times xy{\Large]}
\]
也就相当于把这个式子拆成了四个部分:
\[(i+1)(j+1)×\sum_{x=1}^{i}\sum_{y=1}^{j}d[x,y]
\]
\[-(j+1)×\sum_{x=1}^{i}\sum_{y=1}^{j}(d[x,y]\times x)
\]
\[-(i+1)×\sum_{x=1}^{i}\sum_{y=1}^{j}(d[x,y]\times y)
\]
\[\sum_{x=1}^{i}\sum_{y=1}^{j}(d[x,y]\times xy)
\]
所以我们只需要四个树状数组 \(c1[i,j],c2[i,j],c3[i,j],c4[i,j]\) 分别维护 \(d[i,j],d[i,j]\times i,d[i,j]\times j,d[i,j]\times ij\) 即可。
代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e3+50;
int n, m, c1[N][N], c2[N][N], c3[N][N], c4[N][N];
int lowbit(int k) {return k&-k;}
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j)) {
c1[i][j] += d;
c2[i][j] += d*x;
c3[i][j] += d*y;
c4[i][j] += d*x*y;
}
}
int ask(int x, int y) {
int sum = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
sum += (x+1)*(y+1)*c1[i][j]-(y+1)*c2[i][j]-(x+1)*c3[i][j]+c4[i][j];
return sum;
}
signed main() {
ios::sync_with_stdio(0);
cin >> n >> m;
int opt, x1, y1, x2, y2, k;
while (cin >> opt >> x1 >> y1 >> x2 >> y2) {
if (opt == 1) {
cin >> k;
add(x1, y1, k);
add(x1, y2+1, -k);
add(x2+1, y1, -k);
add(x2+1, y2+1, k);
}
else cout << ask(x2, y2)-ask(x1-1, y2)-ask(x2, y1-1)+ask(x1-1, y1-1) << '\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号