P1879 [USACO06NOV] Corn Fields G

P1879 [USACO06NOV] Corn Fields G

首先考虑暴搜，枚举每个点种不种草，再判断是否有没有相邻的。

我们会发现，只有 \(n\) 个点对答案有影响，为点 \((i,j)\) 上方的点 \((i-1,j)\) 到点 \((i-1,n)\) 及点 \((i,1)\) 到点 \((i,j)\)。如下图所示，只有红色块会对黄色块影响（图丑，见谅）。

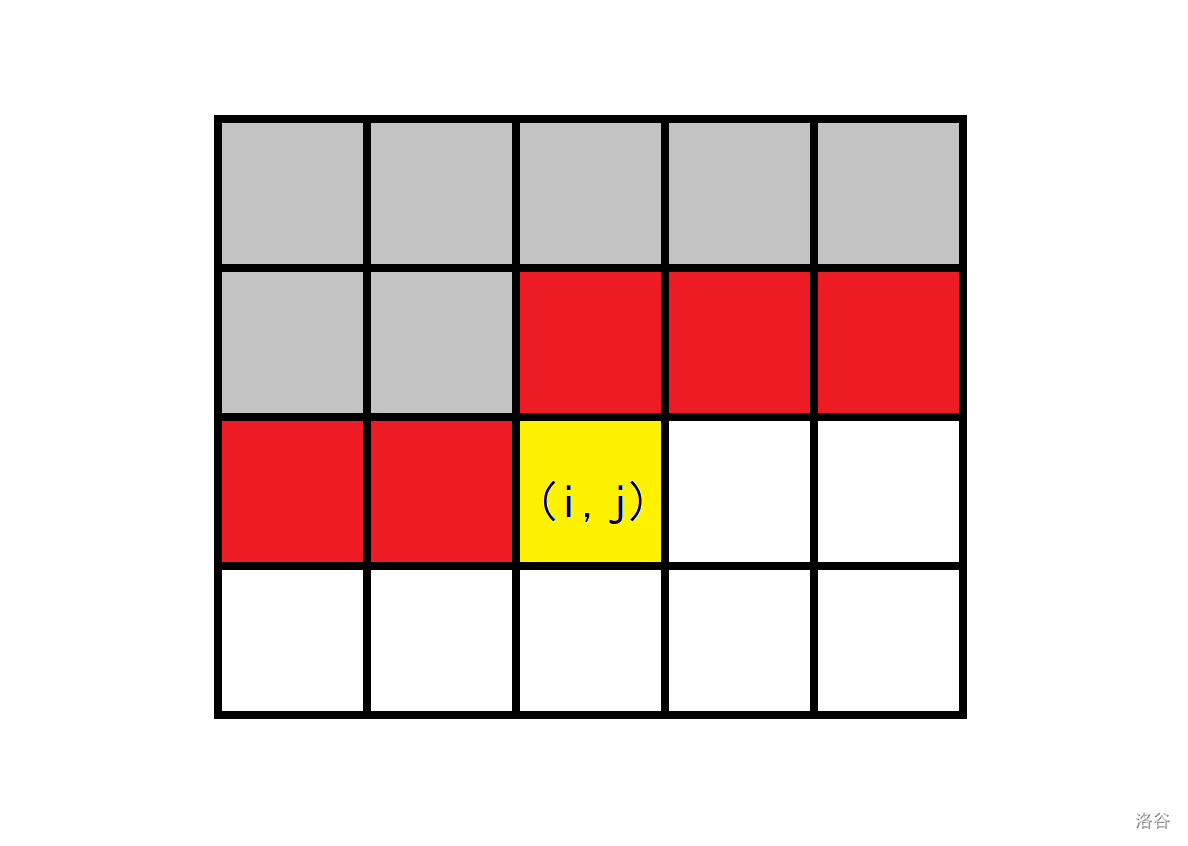
那么我们就可以状态压缩了，只记录位置以及红色块信息。这里定义 \(1\) 为种草，\(0\) 为不种草。令 \(f_{i,j,state}\) 为当前位置为点 \((i,j)\)，红色块状态为 \(state\)（最低位到最高位为矩阵中从上到下，从左到右的顺序）。

若当前点要种草，有以下限制：

• 输入矩阵的这一位必须为 \(1\)

• 若点不在第一行，那么点上面一格必须为 \(0\)

• 若点不在第一列，那么点左边一格必须为 \(0\)

若不种草，则没有限制，直接转移即可。

这类 dp 被称为轮廓线 dp。

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 15, mod = 1e8;
int n, m, ans, a[N][N], f[N][N][1<<N];

int main() {
	ios::sync_with_stdio(0);
	cin >> m >> n;
	for (int i = 1; i <= m; ++i)
		for (int j = 1; j <= n; ++j)
			cin >> a[i][j];
	f[0][n][0] = 1;
	for (int i = 1; i <= m; ++i)
		for (int j = 1; j <= n; ++j) {
			int x = i, y = j-1;
			if (!y) --x, y = n;
			for (int k = 0; k < 1<<n; ++k) {
				f[i][j][k>>1] = (f[i][j][k>>1]+f[x][y][k])%mod;
				if (!a[i][j] || (k&1)) continue;
				if (j != 1 && (k>>n-1&1)) continue;
				f[i][j][(k>>1)|(1<<n-1)] = (f[i][j][(k>>1)|(1<<n-1)]+f[x][y][k])%mod;
			}
		}
	for (int i = 0; i < 1<<n; ++i) ans = (ans+f[m][n][i])%mod;
	cout << ans;
	return 0;
}