区区区间间间（单调栈）

题目链接

题目描述：

Input：

第一行输入数据组数T
对于每组数据，第一行为一个整数n，表示序列长度
接下来一行有n个数，表示序列内的元素

Output：

对于每组数据，输出一个整数表示答案

Example：

Input：

3
3
4 2 3
5
1 8 4 3 9
20
2 8 15 1 10 5 19 19 3 5 6 6 2 8 2 12 16 3 8 17

output：

5
57
2712

思路：

思路：
就是求所有子区间(区间长度大于1的子区间)的最大值减去最小值的和是多少。

我们对原式子拆分一下可得

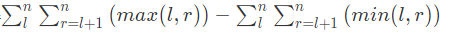
其中max(l,r)表示区间l到r的最大值，min(l,r)表示区间l到r的最小值
考虑单调栈，单调栈维护什么？ 维护以a[i]为区间的最大值，往左右两边去更新拓展。
正着跑一次单调栈，倒着跑一次单调栈就能维护出来l和r数组。
其中l[i]表示以a[i]为最大值，左边最多延伸到l[i]，r[i]表示以a[i]为最大值，右边最多延伸到r[i]
然后怎么计算呢？
有两种情况。
① a[i]作为一个区间的端点，那么可以选择的区间另一个端点就是r[i]-l[i]。
② a[i]作为区间中的一点，也就是区间的端点都没选。那么就是在l[i]到i之间选一个作为左端点，r[i]-i之间选一个作为右端点，乘法原理可得区间的个数为 (r[i]-i) * (i-l[i])
这样就处理出来拆分出来的和式的第一部分了。
第二部分怎么求？
让a[i]=-a[i]，那么求最小值，就等于取反后的求最大值，在跑一下上面的过程就好了。

#include<bits/stdc++.h>
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
using namespace std;
typedef unsigned long long ull;
typedef  long long ll;
typedef pair<ll,ll> pi;
#define IOS std::ios::sync_with_stdio(false)
#define ls p<<1
#define rs p<<1|1
#define mod 1000000000 + 7
#define PI acos(-1.0)
#define INF   1e9
#define N 200000 + 5
/*********************Code*********************/
ll t,n,ans,a[N],l[N],r[N];
ll solve(){
    for(ll i = 1;i <=n;i++){
        ll j = i;
        while(j>1&&a[j-1]<=a[i])
            j = l[j-1];
        l[i] = j;
    }
    for(ll i = n;i>=1;i--){
        ll j = i;
        while(j<n&&a[j+1]<a[i])// 比较中不加等号，是为了避免下一位相同的数在计算的过程中重复运算
            j = r[j+1];
        r[i] = j;
    }
    ll sum = 0;
    for(ll i = 1;i <= n;i++){
        sum +=a[i]*(r[i]-l[i]);
        sum +=a[i]*(i-l[i])*(r[i]-i);
    }
    return sum;
}
int main(void){
    IOS;
    cin>>t;
    while(t--){
        cin>>n;
        for(ll i = 1;i <= n;i++)
            cin>>a[i];
        ans = solve();
        for(ll i = 1;i <=n;i++)
            a[i] *=-1;
        ans +=solve();
        cout<<ans<<endl;
    }
    return 0;
}