Battle for Wosneth2【概率】-2020百度之星复赛

题意

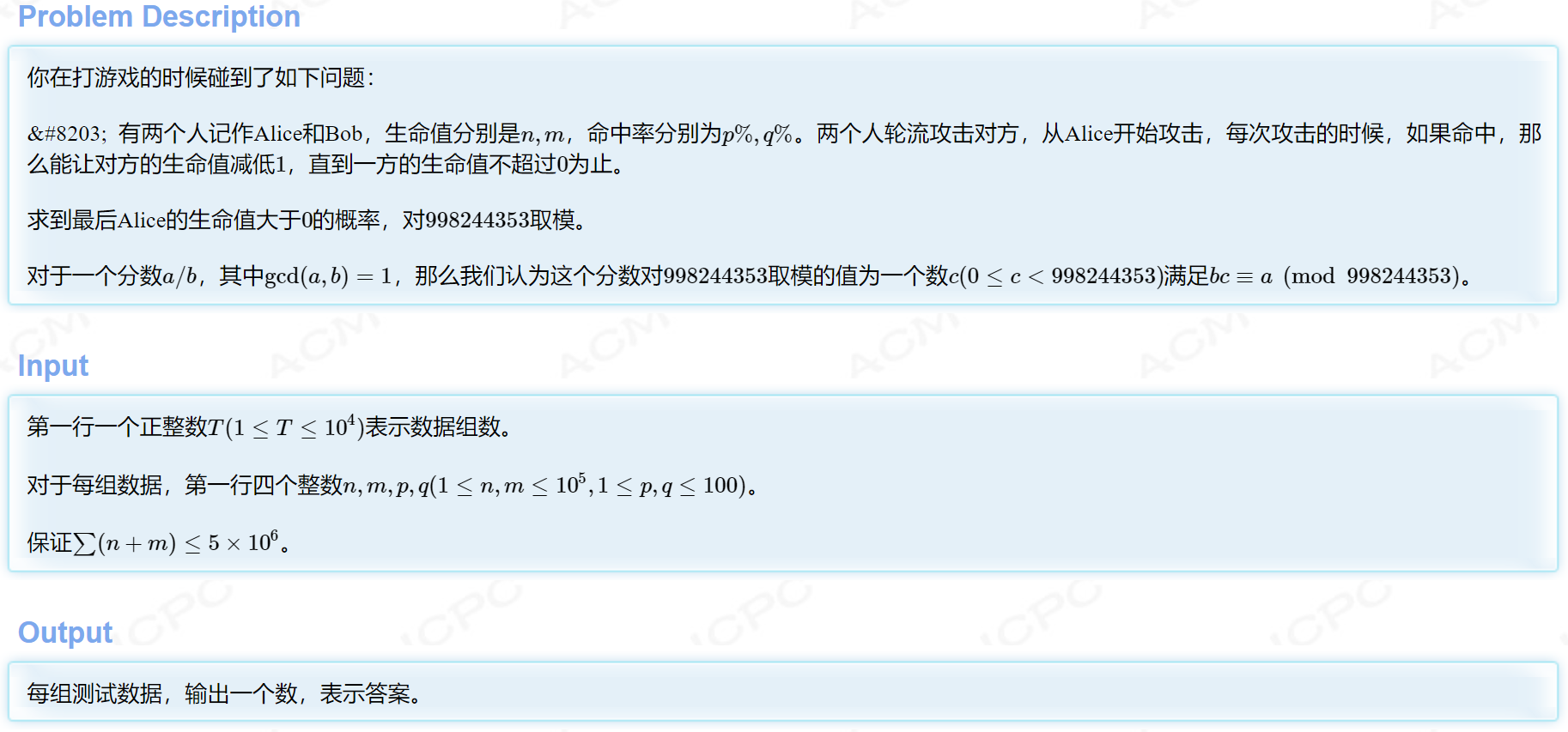
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6842

分析

考虑一个二维的 \(DP\) 模型，每次对连续两轮进行分析。如果两个人都没有打中对方，没有意义。而且最终二者的状态一定是 \((r,1)\)，然后 \(Alice\) 一枪把 \(Bob\) 干掉。所以对于 \((i,j)\)，有三种后继状态：

• \((i-1,j-1)\)，转移的概率为 \(a=\frac{pq}{1-(1-p)(1-q)}\)
• \((i,j-1)\)，转移的概率为 \(b=\frac{p(1-q)}{1-(1-p)(1-q)}\)
• \((i-1,j)\)，转移的概率为 \(c=\frac{(1-p)q}{1-(1-p)(1-q)}\)

最后，\(Alice\) 一枪打死 \(Bob\) 的概率为 \(d=\frac{p}{1-(1-p)(1-q)}\)。

我们先计算出 \((n,m)\to (r,1)\) 的概率，然后再计算 \((r,1)\to (r,0)\) 的概率。

下面对上述的三种转移方式的次数进行讨论，假设第一种方式的次数为 \(x\)，那么第二种方式的次数为 \(m-1-x\)，第三种方式的次数为 \(n-r-x\)。令 \(i=n-r\)，则概率如下：

\[\begin{align} P & = \sum_{i=0}^{n-1}{\sum_{x=0}^{\min(m-1,i)}{C(m-1+i-x,i-x)·C(m-1,x)·a^x·b^{m-1-x}·c^{i-x}}} \end{align} \]

此时，无法直接处理，考虑改变枚举顺序，同时令第三种方式的次数为 \(i\)，有：

\[\begin{align} P & = \sum_{x=0}^{\min(n-1,m-1)}{C(m-1,x)·a^x·b^{m-1-x}\sum_{i=0}^{n-1-x}{C(m-1-i,i)·c^i}} \end{align} \]

令 \(S(r)=\sum_{i=0}^{r}{C(m-1-i,i)·c^i}\)，可以预处理。最终答案为：

\[\begin{align} P & =d· \sum_{x=0}^{\min(n-1,m-1)}{C(m-1,x)·a^x·b^{m-1-x}·S(n-1-x)} \end{align} \]

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int N=1e5+5;
const int mod=998244353;
const int inv100=828542813;
ll sum[N],fac[N<<1],inv[N];
int n,m;
ll p,q,a,b,c,d;
ll power(ll x,ll y)
{
    ll res=1;
    x%=mod;
    while(y)
    {
        if(y&1) res=res*x%mod;
        x=x*x%mod;
        y>>=1;
    }
    return res;
}
void init()
{
    int maxn=1e5,up=2e5;
    fac[0]=1;
    for(int i=1;i<=up;i++)
        fac[i]=fac[i-1]*i%mod;
    inv[maxn]=power(fac[maxn],mod-2);
    for(int i=maxn-1;i>=0;i--)
        inv[i]=inv[i+1]*(i+1)%mod;
}
ll solve()
{
    //预处理sum
    sum[0]=1;
    ll tc=1;
    for(int i=1;i<n;i++)
    {
        tc=tc*c%mod;
        ll ci=fac[m-1+i]*inv[i]%mod*inv[m-1]%mod;
        sum[i]=(sum[i-1]+ci*tc%mod)%mod;
    }
    int minn=min(n-1,m-1);
    ll ta=1,tb=power(b,m-1);
    ll ans=tb*sum[n-1]%mod;
    ll ib=power(b,mod-2);
    for(int i=1;i<=minn;i++)
    {
        ta=ta*a%mod;
        tb=tb*ib%mod;
        if(i==m-1&&b==0) tb=1;//注意
        ll ci=fac[m-1]*inv[m-1-i]%mod*inv[i]%mod;
        ans=(ans+ci*ta%mod*tb%mod*sum[n-1-i]%mod)%mod;
    }
    return ans;
}
int main()
{
    int T;
    scanf("%d",&T);
    init();
    while(T--)
    {
        scanf("%d%d%lld%lld",&n,&m,&p,&q);
        p=p*inv100%mod;
        q=q*inv100%mod;
        ll t=power(1-(1-p)*(1-q)%mod+mod,mod-2);
        a=p*q%mod*t%mod;
        b=(p*(1-q)%mod*t%mod+mod)%mod;
        c=((1-p)*q%mod*t%mod+mod)%mod;
        d=p*t%mod;
        ll ans=d*solve()%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

参考博客：https://www.cnblogs.com/Lanly/p/13473041.html#e-battle-for-wosneth2-hdu-6842