P3863 序列 题解

原题链接

我们进行一个分块大学习

如果题目中的序列是一个数，那么这就变成了分块板题，查询区间内大于等于 \(c\) 的数有多少个，这个可以分块加二分来解决，但现在我们要一下子搞一个序列，首先考虑把询问离线，依次处理每个数，相当于我们只维护了一个时间轴，在进行一系列加操作后回答当前区间的查询。

接着我们发现每次加操作是作用在一定范围内的，把每次操作的作用范围和查询的覆盖范围在“序列-时间”的二维平面上表示出来如下图所示。

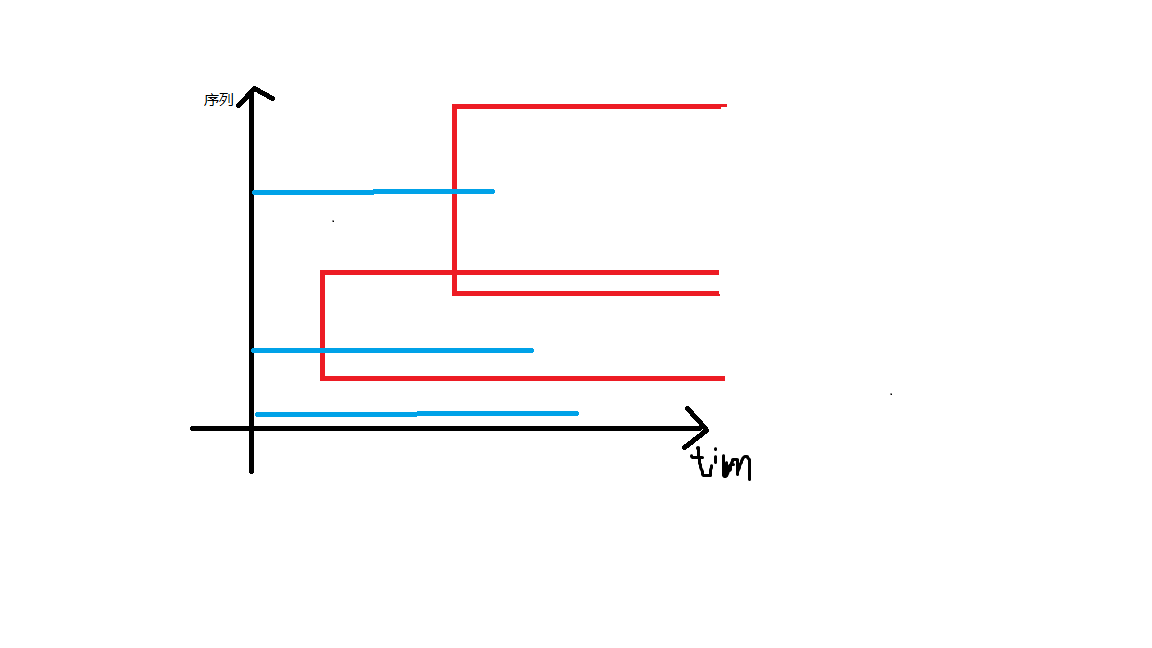
红色表示加操作，蓝色表示一次询问。
既然我们只维护了一根时间轴，肯定是无法做到像上图这种矩形加的操作的，考虑差分，假设一个加操作作用在序列的区间 \([l,r]\) 上，当处理到序列上第 \(l\) 个数时就会对时间轴上 \((t,q)\) 的区间产生贡献，直到处理到 \(r+1\) 个数时会将此贡献消除，实际上就是通过差分把一次矩形加的操作转换成了两次区间操作。（上文的 \(t,q\) 分别表示当前操作出现的时间和最后一个操作的时间）

所以总的算法就是，先将询问离线，把询问和操作都按照序列上的位置排序，在依次枚举序列上的数字处理询问，查询时将时间轴分块即可。

点击查看代码

const int N=1e5+5;
struct add{
    int x,l,r,v;
    bool operator <(const add &G) const{
        return x<G.x;
    }
}todo[N<<1];
int tod;
struct query{
    int x,l,r,v,id;
    bool operator <(const query &G) const{
        return x<G.x;
    }
}que[N];
int toq;
int n,q;
int a[N],b[N],add[500],tmp[N],pos[N],L[500],R[500];
int tot,len;
int ans[N],toa;
bool cmp(int x,int y){
    return x>y;//块内从大到小排序
}
ili void sort_block(int p){
    for(int i=L[p];i<=R[p];i++) tmp[i]=b[i];
    sort(tmp+L[p],tmp+R[p]+1,cmp);
}
ili void init(){
    len=sqrt(q);
    for(int i=1;i<=q;i++) pos[i]=(i-1)/len+1;
    for(int i=1;i<=pos[q];i++) L[i]=(i-1)*len+1,R[i]=min(i*len,q);
    tot=pos[q];
    //初始都为空，无需排序
}
ili void update(int l,int r,int v){
    int x=pos[l],y=pos[r];
    if(x==y){
        for(int i=l;i<=r;i++) b[i]+=v;
        sort_block(x);  
    }else{
        for(int i=x+1;i<=y-1;i++) add[i]+=v;
        for(int i=l;i<=R[x];i++) b[i]+=v;
        for(int i=L[y];i<=r;i++) b[i]+=v;
        sort_block(x),sort_block(y);
    }
}
ili int query(int l,int r,int c){
    int x=pos[l],y=pos[r],ans=0;
    if(x==y){
        for(int i=l;i<=r;i++) if(b[i]+add[x]>=c) ans++;
    }else{
        for(int i=l;i<=R[x];i++) if(b[i]+add[x]>=c) ans++;
        for(int i=L[y];i<=r;i++) if(b[i]+add[y]>=c) ans++;
        for(int i=x+1;i<=y-1;i++){
            int l=L[i]-1,r=R[i]+1;
            while(r-l>1){
                int mid=(l+r)>>1;
                if(tmp[mid]+add[i]>=c){
                    l=mid;
                }else{
                    r=mid;
                }
            }
            ans+=(l-L[i])+1;
        }
        
    }
    return ans;
}
void xpigeon(){
    rd(n,q);
    q++;//1-index
    for(int i=1;i<=n;i++){
        rd(a[i]);
    }
    init();
    for(int i=2,opt,l,r,x,p,y;i<=q;i++){
        rd(opt);
        if(opt==1){
            rd(l,r,x);
            todo[++tod]={l,i,q,x};
            todo[++tod]={r+1,i,q,-x};
        }else{
            rd(p,y);
            //过去有多长时间大于等于y-a[p]
            que[++toq]={p,1,i-1,y-a[p],++toa};
        }
    }
    sort(todo+1,todo+tod+1),sort(que+1,que+toq+1);
    //依次考虑序列上每个数
    for(int i=1,idxd=1,idxq=1;i<=n;i++){
        //先进行所有与i相关的add操作，随后在时间序列上回答对应询问
        while(todo[idxd].x==i){
            update(todo[idxd].l,todo[idxd].r,todo[idxd].v);
            idxd++;
        }
        while(que[idxq].x==i){
            ans[que[idxq].id]=query(que[idxq].l,que[idxq].r,que[idxq].v);
            idxq++;
        }
    }
    for(int i=1;i<=toa;i++){
        cout<<ans[i]<<'\n';
    }
}

总体时间复杂度 \(O(n\sqrt {n \log n})\)