图
0. PTA得分截图

1.本周学习总结
1.1 总结图内容
图的概念:
线性结构可以看成是树形结构的特殊情况。
树形结构可以看成是图形结构的特殊情况。
图形结构是最普遍的 一类数据结构,具有广泛的实际应用。
图的分类:
有向图:弧是有方向的边
无向图:没方向的边
完全图:
无向图:有n(n-1)/2条边
有向图:有n(n-1)条边
稠密图:当一个图接近完全图时,则称为稠密图
稀疏图:当一个图的边e<<n(n-1)时,则称为稀疏图
强连通图:有向图中的任意两个顶点,都有去往彼此的路径。
强连通分量:各个强连通子图称作它的强连通分量。如下图,有三个强连通分量·

图的基本术语:
度:
无向图:以该顶点为端点的边数成为该顶点的度
有向图:
入度:以顶点i为终边的入边的数目,称为该顶点的入度
出度:以顶点i为起始点的出边的数目,称为该顶点的出度
图的存储结构:
邻接矩阵:
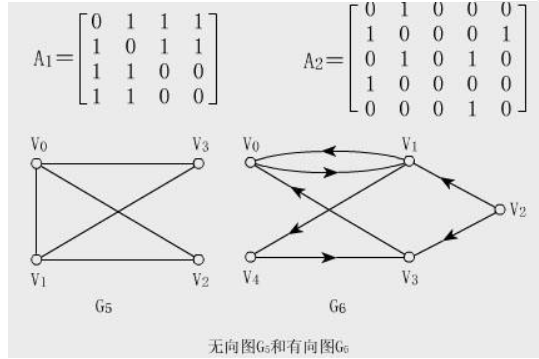
- 邻接矩阵用二维数组进行表示
- 每个存储单元存放着顶点i与顶点j的关系,1表示直连,0表示无连边
- 对于无向图的邻接矩阵,会发现关于对角线对称。
- 时间复杂度:O(n^2)
邻接矩阵存储类型的定义及创建邻接矩阵
#defineMAXV
//声明顶点的类型
typedef struct
{
int no; //顶点编号
InfoType info; //顶点其它信息
}VetexType;
声明邻接矩阵的类型
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接定义
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
}MatGraph;
MatGraph g; //声明邻接矩阵存储的图
void CreateMGraph(MGraph& g, int n, int e)//建图
{
int i, j;
int a, b;
for ( i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
g.edges[i][j] = 0;
}
}
for (i = 0; i < e; i++)
{
cin >> a >> b;
g.edges[a - 1][b - 1] = b;
g.edges[b - 1][a - 1] = a;
}
g.e = e;
g.n = n;
}
邻接表:
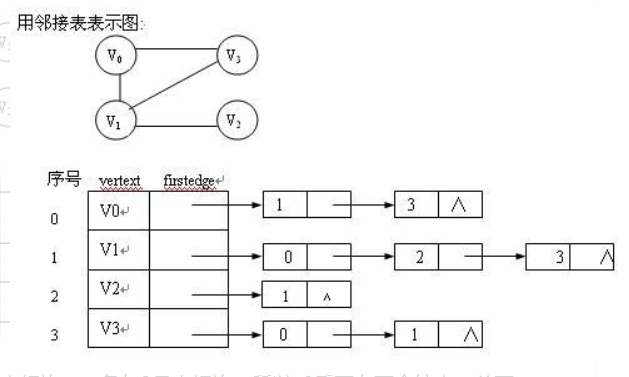
- 对于每个顶点i建立一个单链表,将顶点i的所有邻接点用链存储起来。
- 时间复杂度:O(n+e)
邻接表的存储类型的定义及创建邻接表
//声明邻接表头结点类型
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
}VNode;
//声明边节点类型
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode *nextarc;//指向下一条边的指针
InfoType info;//该边的权值等信息
}ArcNode;
声明图邻接表类型
typedef struct
{
Vnode adjlist[MAXV]; //邻接表
int n,e;
}AdjGraph;
AdjGraph *G;//声明一个邻接表存储的图G
void CreateAdj(AdjGraph*& G, int n, int e)//创建图邻接表
{
int i, j, a, b;
ArcNode* p;
G = new AdjGraph;
for (i = 0; i < n; i++)
{
G->adjlist[i].firstarc = NULL;//给邻接表中所有头结点的指针域置初值
}
for (i = 0; i < e; i++)//根据输入边建图
{
cin >> a >> b;
p = new ArcNode;
p->adjvex = a;
p->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = p;
}
G->e = e;
G->n = n;
}
void DelAdj(AdjGraph*& G, int n, int e) //删除邻接表
{
ArcNode* p, * q;
for (int i = 1; i <= n; i++)
{
p = G->adjlist[i].firstarc;
while (p != NULL)
{
q = p;
p = p->nextarc;
delete q;
}
}
delete[] G->adjlist;
}
图的遍历及应用
连通图的深度搜索遍历:
(1)从图中 某个初始顶点v出发,首先访问初始顶点v
(2)选择一个与顶点v相邻且没被访问过的顶点w为初始顶点,再从w出发进行深度优先搜索,直到图中与当前顶点v邻接的所有顶点都被访问过为止。
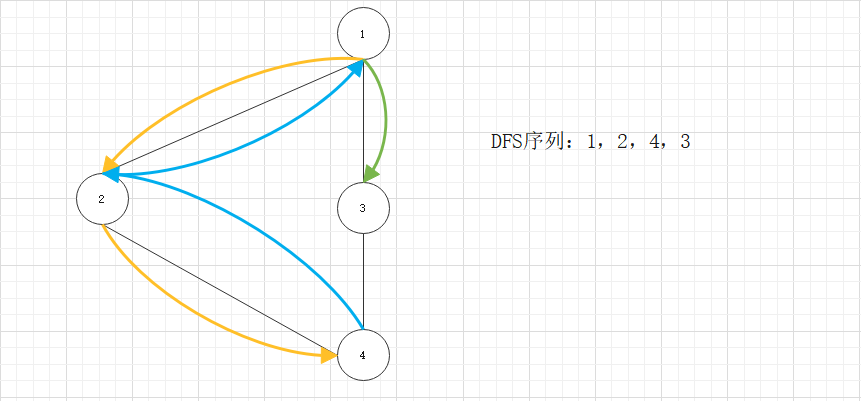
void DFS(ALGraph *G,int v)
{
ArcNode *p;
visited[v]=1;
cout<<" "<<v;
p=G->adjlist[v].firstarc;
while(p!=NULL)
{
if(visited[p->adjvex]==0)
DFS(G,p->adjvex);
p=p->nextarc;
}
}
非连通图的深度优先搜索遍历
void DFSTraverse(Graph G)
{
for(v=0;v<G.vexnum;++v)
{
visited[v]=FALSE;
}
for(v=0;v<G.vexnum;v++)
{
if(!visited[v])
DFS(G,v);
}
}
连通图的广度优先搜索遍历
(1)访问初始点v,接着访问v的所有未被访问过的邻接点。
(2)按照次序访问每一个顶点的所有未被访问过的邻接点。
(3)一次类推,直到图中所有顶点都被访问过。

int visited[MAXV];
void DFS(ALGraph *G,int v)
{
ArcNode *p;
visited[v]=1;
cout<<" "<<v;
p=G->adjlist[v].firstarc;
while(p!=NULL)
{
if(visited[p->adjlist]==0)GFS(G,p->adjvex);
p=p->nextarc;
}
}
非连通图的广度优先搜索遍历
void BFS(AdjGraph *G)
{
int i;
for(i=0;i<G->n;i++)
{
if(visited[i]==0)
{
BFS(G,i);
}
}
}
- 调用BFS()的次数,恰好等于连通分量的个数
采用BFS遍历方式判断无向图是否连通
int map[MAXV][MAXV];
bool Connected(int v)
{
int count=0;
int i.j;
queue<int>q;
q.push(v);
mark[v]=1;
while(!q.empty())
{
v=q.front();
q.pop();
mark[v]=1;
count++;
for(i=1;i<=n;i++)
{
if(!mark[i]&&map[v][i]!=0)
{
q.push(i);
mark[i]=1;
}
}
}
if(count==0)
{
return true;
}
else
return false;
}
采用DFS遍历方式判断无向图是否连通
bool Connect(AdjGraph *G)
{
int i;
bool flag=true;
for(i=0;i<G->n;i++)
{
visited[i]=0;
}
DFS(G,0);//从0开始深度遍历
for(i=0;i<G->n;i++)
{
flag=false;
break;
}
return flag;
}
广度优先遍历找到的路径一定是最短路径,而深度优先遍历则不一定。
深度优先遍历能找到所有路径,而广度优先遍历难以实现。
查找最短路径
查找简单路径
void FindAllPath(AGraph *G,int u,int v,int path[],int d)
{
//d表示path中的路径长度,初始值为-1
int w,i;
ArcNode *p;
d++;
path[d]=u; //路径长度d到u的距离
visited[u]=1;
if(u==v&&d>=1)//找到一条路
{
for(i=0;i<=d;i++)
{
cout<<" "<<path[i];
}
cout<<endl;
}
p=G->adjlist[u].firstarc;
while(p!=NULL)
{
w=p->adjvex; //w为u的相邻顶点
if(visited[w]==0) //若w顶点未访问,递归访问它
{
FindAllPATH(G,w,v,path,d);
}
p=p->nextarc;//p指向u的下一个顶点
}
visited[u]=0;//恢复环境
}
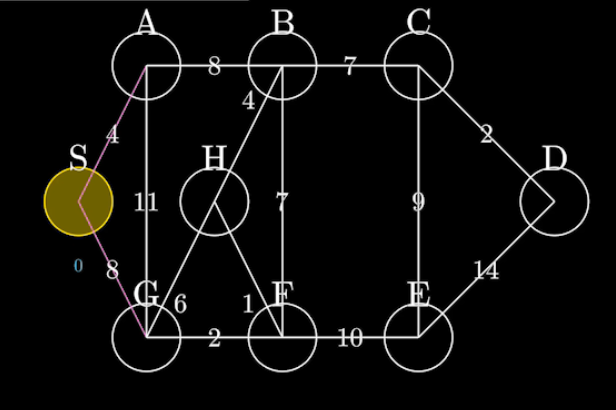
Dijkstras算法(单源最短路径)
1.用邻接矩阵G来表示带权有向图,dis[j]表示从选定的某点v0与j的最短距离,
2.对dis[]进行初始化,dis[i]=G[v] [i]
3.从dis[]里面找最小的dis[j]值(不包括之前找过的点),表示当前求得的一条从v0出发到vj最短路径
然后查看与顶点j相连的其它没被访问的点k,是否与v0直连,如果直连,则比较dis[k]与dis[j]+G[j] [k]
的大小,如果dis[j]+G[v] [k]更小,则说明vo经过中间点j到k比vo直接到k更短,则把dis[k]的值改为dis[j]+G[j] [k]
4.重复上面的操作,知道所有顶点都访问过
5.对于path数组,对path[]数组进行初始化,与顶点v0直连的,path[j]=v0,,不是直连的,置为-1
6.如果发现dis[k]与dis[j]+G[j] [k],则说明vo经过中间点j到k比vo直接到k更短,所以把path[k]的值复制为j,因为path[j]=k的含义表示的是j的上一个全局上距离最短的顶点式k
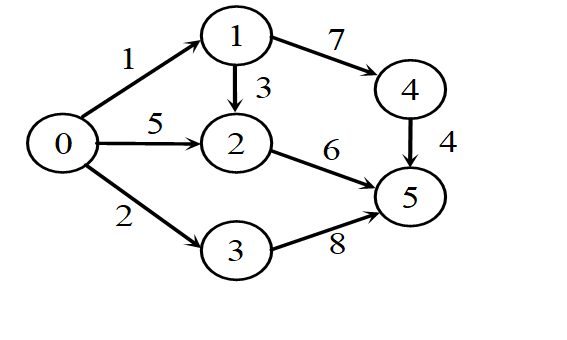
做这个,要注意下标代表的含义
-
0 1 2 3 4 5 0 1 2 3 4 5 S U dis[] path[] 0 1,2,3,4,5 0 1 5 2 ∞ ∞ 0 0 0 0 -1 -1 0,1 2,3,4,5 0 1 4 2 8 ∞ 0 0 1 0 1 -1 0,1,3 2,4,5 0 1 4 2 8 10 0 0 1 0 1 3 0,1,3,2 4,5 0 1 4 2 8 10 0 0 1 0 1 3 0,1,3,2,4 5 0 1 4 2 8 10 0 0 1 0 1 3 0,1,3,2,4,5 0 1 4 2 8 10 0 0 1 0 1 3
void Dijkstra(MatGraph g,int v)
{
int dist[MAXV],path[MAXV];
int visited[MAXV];
int mindis,j,ul
for(i=0;i<g.n;i++)
{
dist[i]=g.edges[v][i]; //距离初始化
visited[i]=0;
if(g.edges[v][i]<INF)
{
path[i]=v; //顶点v到i有边
}
else
{
path[i]=-1; //顶点v到i边
}
}
visited[v]=1;
for(i=0;i<g.n;i++)
{
mindis=INF;
for(j=0;j<g.n;j++)
{
if(s[j]==0&&dist[j]<mindis) //找最小路径长度顶点u
{
u=j;
mindis=dist[j];
}
}
visited[u]=1; //顶点u加入s中
for(j=0;j<g.n;j++)
{
if(s[j]==0)
if(g.edges[u][j]<INF&&dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
}
Dispath(dist,path,s,g.n,v);
}
Dijkstras算法(单源最短路径)特点
- 不适用带负权值的带权图求单源最短路径
- 不适用于求最长路径长度
- 时间复杂度:O(n^2)
Floyd算法->所有顶点间的最短路径
- 我觉得这个算法,其实和Dijkstras算法(单源最短路径)本质上是一样的东西
- 这里介绍一下,两个数组的含义,A[i] [j]存放的是从i到j之间的的最短距离,A[i] [j]>A[i] [k]+A[k] [j],表示的是从i到j之间经过k会更短,所以把A[i] [j]的长度改为A[i] [k]+A[k] [j],path[i] [j]=i,表示的是,全局最短路径中,j顶点的上一个顶点是i。
- 时间复杂度:O(n^3)
void Floyd(MatGraph g)
{
int A[MAXVEX][MAXVEX];//建立A数组
int path[MAXVEX][MAXVEX];
int i,j,k;
for(i=0;i<g.n;i++)
{
for(j=0;j<g.n;j++)
{
A[i][j]=g.edges[i][j];
if(i!=j&&g.edges[i][j]<INF)
{
path[i][j]=i; //i和顶点j之间有一条边
}
else
path[i][j]=-1; //i和j顶点之间没有一条边
}
}
for(k=0;k<g.n;k++)
{
for(i=0;i<g.n;i++)
{
for(j=0;j<g.n;j++)
{
if(A[i][j]>A[i][k]+A[k][j]) //找到更短路径
{
A[i][j]=A[i][k]+A[k][j]; //修改路径长度
path[i][j]=k; //修改经过顶点k
}
}
}
}
}
Bellman-Ford(贝尔曼-福特)
Dijkstra算法是处理单源最短路径的有效算法,但是只局限于边的权值非负的情况,若图中出现权值为负的,则不能实现最短路径,这个算法可以实现
1.数组Distant[i]记录从源点s到顶点i的路径长度,初始化数组Distant[n]为, Distant[s]为0;
2.以下操作循环执行至多n-1次,n为顶点数:
对于每一条边e(u, v),如果Distant[u] + w(u, v) < Distant[v],则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值;
若上述操作没有对Distant进行更新,说明最短路径已经查找完毕,或者部分点不可达,跳出循环。否则执行下次循环;3.为了检测图中是否存在负环路,即权值之和小于0的环路。对于每一条边e(u, v),如果存在Distant[u] + w(u, v) < Distant[v]的边,则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
松弛计算:

松弛计算之前,点B的值是8,但是点A的值加上边上的权重2,得到5,比点B的值(8)小,所以,点B的值减小为5。这个过程的意义是,找到了一条通向B点更短的路线,且该路线是先经过点A,然后通过权重为2的边,到达点B。
当然,如果出现一下情况:
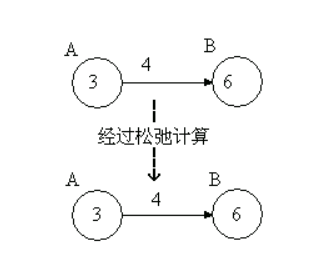
则不会修改点B的值,因为3+4>6。
Bellman-Ford算法可以大致分为三个部分
第一,初始化所有点。每一个点保存一个值,表示从原点到达这个点的距离,将原点的值设为0,其它的点的值设为无穷大(表示不可达)。
第二,进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。
第三,遍历途中所有的边(edge(u,v)),判断是否存在这样情况:d(v) > d (u) + w(u,v),存在则返回false,表示途中存在从源点可达的权为负的回路。
之所以需要第三部分,是因为,如果存在从源点可达的权为负的回路。则应为无法收敛而导致不能求出最短路径。
考虑如下的图:

经过第一次遍历后,点B的值变为5,点C的值变为8,这时,注意权重为-10的边,这条边的存在,导致点A的值变为-2。(8+ -10=-2)
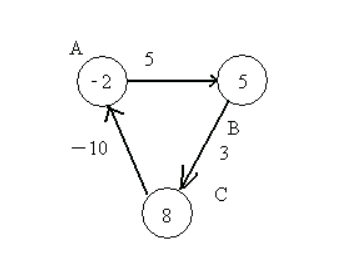
第二次遍历后,点B的值变为3,点C变为6,点A变为-4。正是因为有一条负边在回路中,导致每次遍历后,各个点的值不断变小。
在回过来看一下bellman-ford算法的第三部分,遍历所有边,检查是否存在d(v) > d (u) + w(u,v)。因为第二部分循环的次数是定长的,所以如果存在无法收敛的情况,则肯定能够在第三部分中检查出来。比如
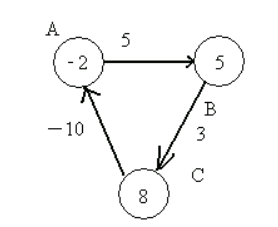
此时,点A的值为-2,点B的值为5,边AB的权重为5,5 > -2 + 5. 检查出来这条边没有收敛。
所以,Bellman-Ford算法可以解决图中有权为负数的边的单源最短路径问。
int N, M;
typedef struct node
{
int u, v;
int cost;
} E;
node E[N];
int dis[N], pre[N];
bool Bellman()
{
int ok;
for(int i = 1; i <= N; ++i)
dis[i] = (i == 1 ? 0 : MAX);
for(int i = 1; i <= N - 1; ++i)
{
ok=1;
for(int j = 1; j <= M; ++j)
if(dis[E[j].v] > dis[E[j].u] + E[j].cost)
{
dis[E[j].v] = dis[E[j].u] + E[j].cost;
ok=0;
}
if(ok==1)
break;
}
bool flag = 1;
for(int i = 1; i <= M; ++i)
if(dis[E[i].v] > dis[E[i].u] + E[i].cost)
{
flag = 0;
break;
}
return flag;
}
int main()
{
cin>>N>>M;
for(int i = 1; i <= M; ++i)
cin>>E[i].u>>E[i].v>>E[i].cost;
if(Bellman())
cout<<dis[M];
else
cout<<"存在负";
return 0;
}
最小生成树
最短路径与最小生成数不同,路径上不一定包含n个顶点
一个连通图的生成树是一个极小连通子图,它含有图中n个顶点和构成一棵树的n-1条边,不能回路
一个连通图的生成树不一定是唯一的
权值和最小的生成树称作最小生成树
最小生成树不一定唯一,但最小生成树的权值之和一定相同
Prim算法

#define INF 0x3f3f3f
void Prim(MGraph g,int v)
{
int lowcost[MAXV],min,closest[MAXV],i,j,k;
for(i=0;i<g.n;i++)
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for(i=1;i<g.n;i++) //找出n-1个顶点
{
min=inf;
for(j=0;j<g.n;j++) //在V-U中找出离U最近的顶点k
{
if(lowcost[j]!=0&&lowcost[j]<min)
{
min=lowcost[j]; //k记录最近顶点编号
k=j;
}
}
lowcost[k]=0; //标记k已经加入U
for(j=0;j<g.n;j++) //修正
{
if(lowcost[j]!=0&&g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
}
特点:
- 局部最优(贪心算法)+调整=全局最优
- 贪心算法:只顾或者眼前最大的利益,有时不一定是最优解
- 时间复杂度:O(n^2),适用于稠密图
- 应用:公路村村通
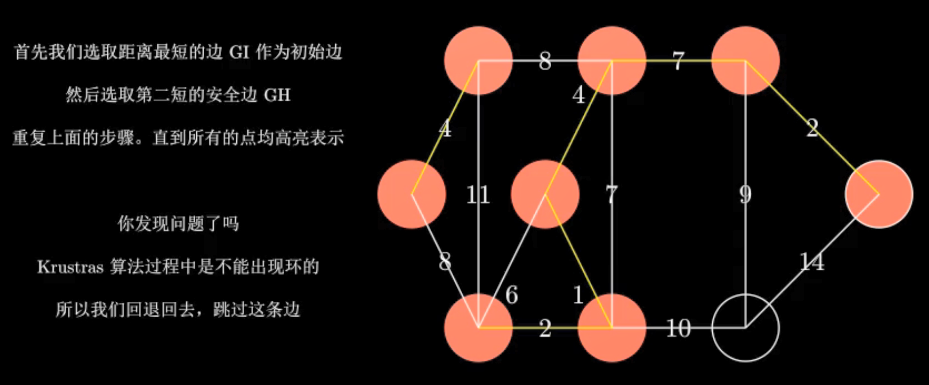
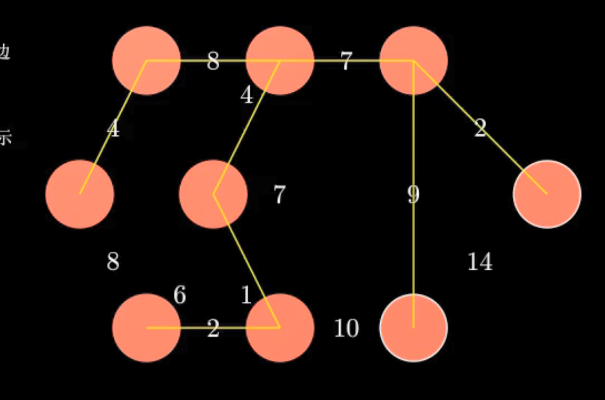
Kruskal算法
#include<iosream>
#include<vector>
#include<algorithm>
#define MAX N 100
using namespace std;
struct Node
{
int numr;
int numd;
int val;
}
int cmp(Node a,Node b) //对vector存储内容进行由小到大排序
{
return a.val<b.val;
}
vector<Node>v;//保存所有边的信息
int F[MAX_N];
int findPar(int n)
{
if(F[n]=n)
{
return F[n];
}
else
{
F[n]=findPar(F[n]);//减少下次查找的时间
return F[n];
}
}
/*如果两个节点不在用一个连通分支中,则合并,并修改其中一棵树根节点的父亲节点 */
int merges(int a,int b)
{
int x=findPar(a);
int y=findPar(b);
if(x==y)
{
return 1;
}
else
{
F[y]=x;
return 0;
}
}
int main()
{
for(int i=0;i<MAX;i++)
{
F[i]=i;
}
int m;
cin>>m;
for(int i=0;i<m;i++)
{
Node nod;
cin>>nod.numr>>nod.numd>>nod.val;
v.push_back(nod);
}
sort(v.begin(),v.end(),cmp);//权值由小到大排序
for(int i=0;i<v.size();i++)
{
if(!merges(v[i],numr,v[i].numd))
{
v1.push_back(v[i]);
}
}
}
特点:
- 与并查集进行结合
- 时间复杂度O(elog2e),适用于稀疏图
- 应用:公路村村通
拓扑排序
1.从有向图中选取一个没有前驱的顶点,并输出之
2.从有向图中删除此顶点以及所有以他为尾的弧
3.重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止

typedef struct
{
vertex data;
int count;
ArcNode *firstarc;
}VNode;
void TopSort(ADjGraph *G)
{
int i,j;
int St[MAXV];
int top=-1;
ArcNode *p;
for(i=0;i<G->n;i++) //求所有顶点的入度
{
p=G>adjlist[i].firstarc;
while(p!=NULL)
{
G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
for(i=0;i<G->n;i++) //将入度为0的顶点入栈
{
if(G->adjlist[i].count==0)
{
top++;
St[top]=i;
}
}
while(top>-1)
{
i=St[top];
top--;
cout<<i;
p=G->adjlist[j].firstarc;
while(P!=NULL)
{
j=p->adjvex;
G->adjlist[j].count--;
if(G->adjlist[j].count==0)
{
top++;
St[top]=j;
}
p=p->nextarc;
}
}
}
特点:
- 在输出顶底序号的地方加入一个初始化为0的cnt,进行cnt++,如果最后cnt<n,则说明有回路
- 时间复杂度:O(n+e)
- 一个AOV-网的拓扑序列不是唯一的
- 应用:可以检测是否有环
关键路径
用顶点表示事件,用有向边e表示活动,边的权表示活动持续的时间,是带权的有向无环图
关键路径:从有向图的源点到汇点的最长路径
关键活动:关键路径中的边
源点:入度为0
汇点:出度为0
事件的最早开始时间:事件v的最早开始事件,一定是所有前驱事件x,y,z完成,才轮到事件v
ve(v)=max{ve(x)+a,ve(y)+b,ve(z)+c}(从左往右)
事件的最迟开始时间:要保证后继所有事件能按时完成,取最小
vl(v)=min{vl(x)-a,vl(y)-b,vl(z)-c}(从右往左)

| 事件 | ve(取max) | vl(取min) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 19 | 19 |
| 3 | 15 | 15 |
| 4 | 29 | 37 |
| 5 | 38 | 38 |
| 6 | 43 | 43 |
- 特点:关键路径是1->2->3->5->6,因为ve=vl,没有富余的时间
| 活动<v1,v2> | <1,2> | <1,3> | < 3,2> | <2,4> | <2,5> | < 3,5> | <4,6> | <5,6> |
|---|---|---|---|---|---|---|---|---|
| e=v1e | 0 | 0 | 15 | 19 | 19 | 15 | 29 | 38 |
| l=v2l-weight | 17 | 0 | 15 | 27 | 19 | 27 | 37 | 38 |
| l-e | 17 | 0 | 0 | 8 | 0 | 12 | 8 | 0 |
- 特点:关键活动是l-e=0
1.2谈谈你对图的认识和看法
图,这个章节,我们会看到我们开始对于二维数组的认识更深一步,并且,这个章节学习的算法,也比前面几个章节多很多,我们求最短路径,在实际问题里应用甚广,拓扑排序对问题的缓急进行了详细的说明,等等,还有很多算法,我很佩服这些研究算法的人,因为得出一个正确的算法,要经过大量的计算,不只是针对某一个特例,而是对大部分的问题都适用,这些,都要有很扎实的数学功底,并且有耐心的接受来自别人的质问,耐心的接受每一次失败,所以,没有哪个伟人是轻轻松松的,转眼间,我们就已经学到图了,也很快,我的大学的第二个学期也快过去了,可是感觉自己这个学期,什么都没有学到,在家里,玩的玩,吃的吃,这些暂时的快乐总是让我的心很不安,因为你在轻松的时候,别人在努力学习,一步一步的进步,而自己却一步一步的退步,其实心里五味杂陈,不知如何是好,太难了,希望疫情快快过去,,让我的第二个学期的大学生活,可以在大学里说结束。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号