Tarjan缩点【p4819】[中山市选]杀人游戏
Description
一位冷血的杀手潜入Na-wiat,并假装成平民。警察希望能在\(N\)个人里面,查出谁是杀手。警察能够对每一个人进行查证,假如查证的对象是平民,他会告诉警察,他认识的人,谁是杀手,谁是平民。假如查证的对象是杀手,杀手将会把警察干掉。现在警察掌握了每一个人认识谁。每一个人都有可能是杀手,可看作他们是杀手的概率是相同的。
问:根据最优的情况,保证警察自身安全并知道谁是杀手的概率最大是多少?
Input
第一行有两个整数 \(N,M\)。 接下来有\(M\)行,每行两个整数 \(x,y\),表示 \(x\) 认识 \(y\)(\(y\) 不一定认识 \(x\) ,例如President同志) 。
Output
仅包含一行一个实数,保留小数点后面 \(6\) 位,表示最大概率。
首先,如果一些人之间的关系存在环,那么我们可以只问其中的一个人就能知道这个环中的所有人的身份.可以降低我们的被害几率.
环?\(Tarjan\)缩点.
考虑到直接算安全的概率可能比较难算,所以我们考虑单步容斥.
安全概率=1-被杀概率
\(Tarjan\)缩点之后我们再次建图,会得到一个拓扑图.
这个拓扑图中,对于入度为\(0\)的一个点.显然,其会对被害几率有贡献.
因此我们记录图中入度为\(0\)的点的个数.
但是会存在一种情况,类似这样.
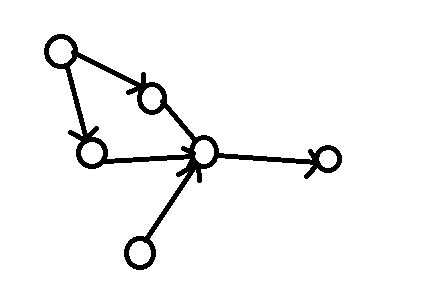
显然这个时候如果我们从左上角的点开始调查,发现没有杀手.
则杀手必定在下边的点中(这个点\(size\)必须为1,并且与其相连的点必须有其他入度).
确保自身安全的情况下,我们已经知道了杀手是谁.因此,这种点对答案并没有贡献.
且至多会有一个,
在代码中判断一下即可.
代码
#include<cstdio>
#include<cctype>
#include<iostream>
#define N 100008
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,m,head[N],tot,ttt,h[N],size[N],col;
struct cod{int u,v;}edge[N<<5],e[N<<2];
inline void add(int x,int y)
{
edge[++tot].u=head[x];
edge[tot].v=y;
head[x]=tot;
}
inline void ado(int x,int y)
{
e[++ttt].u=h[x];
e[ttt].v=y;
h[x]=ttt;
}
int dfn[N],low[N],top,idx,stk[N],ins[N],now,belong[N];
bool inq[N],flg;
void tarjan(int u)
{
dfn[u]=low[u]=++idx;
stk[++top]=u;inq[u]=true;
for(R int i=head[u];i;i=edge[i].u)
{
if(!dfn[edge[i].v])
{
tarjan(edge[i].v);
low[u]=min(low[u],low[edge[i].v]);
}
else if(inq[edge[i].v])
low[u]=min(low[u],dfn[edge[i].v]);
}
if(low[u]==dfn[u])
{
int now=-1;col++;
while(now!=u)
{
now=stk[top--];
size[col]++;
inq[now]=false;
belong[now]=col;
}
}
}
inline bool pd(int x)
{
for(R int i=h[x];i;i=e[i].u)
if(ins[e[i].v]==1)return false;
return true;
}
int ans;
int main()
{
in(n),in(m);
for(R int i=1,x,y;i<=m;i++)
{
in(x),in(y);
add(x,y);
}
for(R int i=1;i<=n;i++)
if(!dfn[i])tarjan(i);
for(R int x=1;x<=n;x++)
for(R int i=head[x];i;i=edge[i].u)
if(belong[edge[i].v]!=belong[x])
ins[belong[edge[i].v]]++,ado(belong[x],belong[edge[i].v]);
for(R int x=1;x<=col;x++)
{
if(!flg and size[x]==1 and !ins[x] and pd(x))flg=true;
if(!ins[x])ans++;
}
if(flg)ans--;
printf("%.6f",1-(double)((double)ans/(double)n));
}
除特殊声明外,本博客作品均由顾z创作。
未经博主允许,不得转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号