2.4 浮点数
2.4.1 二进制小数
理解浮点数的第一步是考虑含有小数值的二进制数字。首先,我们来看看更熟悉的十进制表示法。十进制表示法使用如下形式的表示:dmdm-1…d1d0.d-1d-2d-n。其中每个十进制数di的取值范围是0~9。这个表达描述的数值d定义如下:
![]()
数字权的定义与十进制小数点符号('.' ),这意味着小数点左边的数字的权是10的正幂,得到整数值,而小数点右边的数字的权是10的负幂,得到小数值。例如,12.3410表示数字1*101+2*100+3*10-1+4*10-2=![]()
类似,考虑一个形如bmbm-1…b1b0.b-1b-2…b-n-1b-n的表示法,其中每个二进制数字,或者成为位,bi的范围是0和1,这种表示方法表示的数b的定义如下:
![]()
符号'.' 现在变成了二进制的点,点左边的位的权是2的正幂,点右边的权是2的负幂。例如,101.112表示数字1*22+0*21+1*20+1*2-1+1*2-2=![]() 。
。
从上式可以看出,二进制小数点向左移动一位相当于这个数被2除。例如,101.112表示数![]() ,而10.1112表示数
,而10.1112表示数![]() 。类似,二进制小数点像右移动一位相当于该值乘2。例如1011.12表示数
。类似,二进制小数点像右移动一位相当于该值乘2。例如1011.12表示数![]() 。
。
注意,形如0.11…12的数表示的是刚好小于1的数。例如,0.1111112表示![]() ,我们将用简单的表达法1.0-
,我们将用简单的表达法1.0-![]() 来表示这样的数值。
来表示这样的数值。
假定我们仅考虑有限长度的编码,那么十进制表示法不能准备地表达像1/3和5/7这样的数。类似,小数的二进制表示法只能表示那些能够被写成x*2y的数。其他的值只能够被近似地表示。例如,数字1/5可以用十进制小数0.20精确表示。不过,我们并不能把它准备地表示为一个二进制小数,我们只能近似的表示它,增加二进制的长度可以提高表示的精度。
练习题2.45 填写下表中的缺失的信息
| 小数值 | 二进制表示 | 十进制表示 |
| 1/8 | 0.001 | 0.125 |
| 3/4 | 0.11 | 0.75 |
| 25/16 | 1.1001 | 1.5625 |
| 43/16 | 10.1011 | 2.6785 |
| 9/8 | 1.001 | 1.125 |
| 47/8 | 101.111 | 5.875 |
| 51/16 | 11.0011 | 3.1875 |
2.4.2 IEEE浮点表示
定点表示法不能很有效的表示非常大的数字。例如,表达式5*2100是用101后面跟随100个零的位模式来表示。相反,我们希望通过给定x和y的值,来表示形如x*2y的数。
IEEE浮点标准用V=(-1)s*M*2E的形式来表示一个数:
- 符号(sign) s决定这数是负数(s=1)还是正数(s=0),而对于数值0的符号位解释作为特殊情况处理。
- 尾数(significand) M是一个二进制小数,它的范围是 1~2-
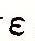 ,或者是0~1-
,或者是0~1- 。
。 -
阶码(exponent) E的作用是对浮点数加权,这个权重是2的E次幂(可能是负数)。将 浮点数的位表示划分为三个阶段,分别对这些值进行编码:
- 一个单独的符号位s直接编码符号s。
- k位的阶码字段exp = ek-1...e1e0编码阶码E。
- n位的小数字段frac=fn-1...f1f0编码尾数M,但是编码出来的值也依赖于阶码字段的值是否等于0。
图示给出了将三个装进字中最常见的格式。在单精度浮点格式(C语言中的float)中,s、exp、和frac字段分别为1位、k=8和n=23位,得到一个32位的表示。在双进度浮点格式(C语言的double)中,s、exp和frac字段分别为1位、k=11位和n=52位,得到一个64位的表示

给定位表示,根据exp的值,被编码的值可以分成三种不同的情况(最后一种情况有两个变种)
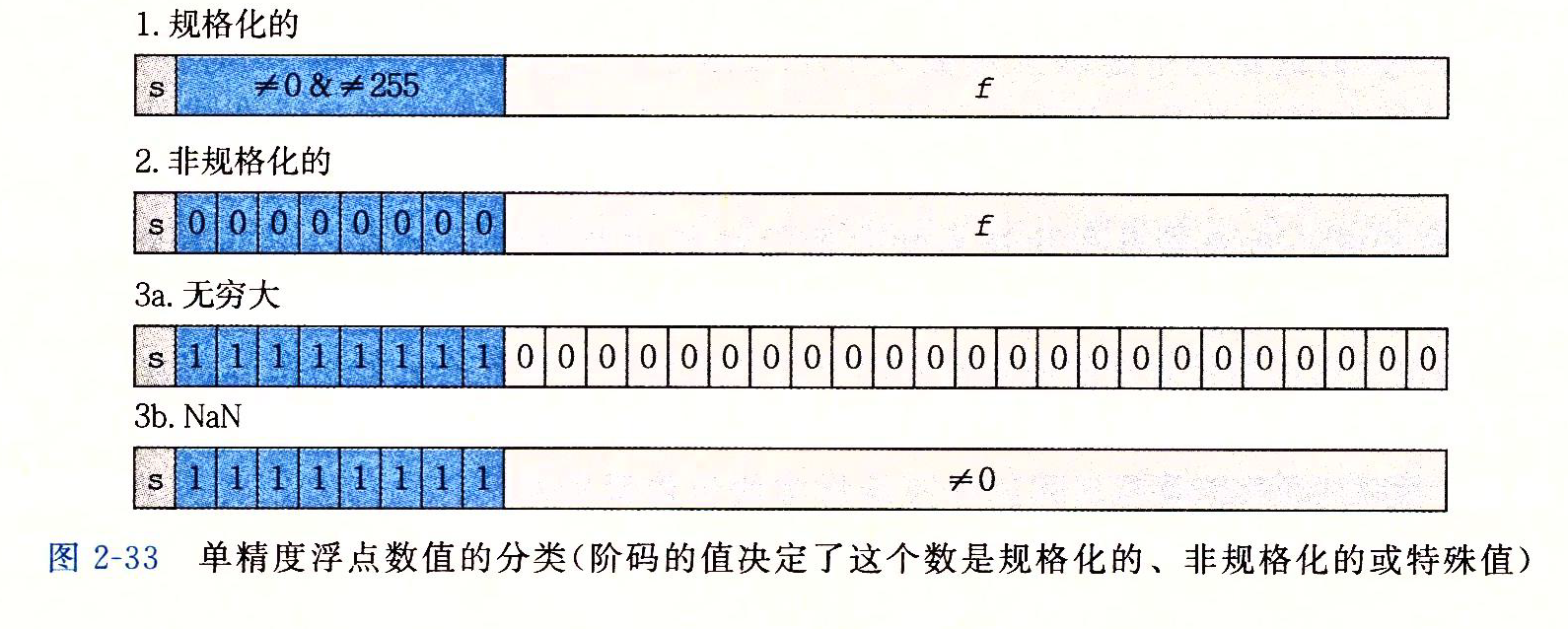 情况1:规格化的值
情况1:规格化的值
当exp的位模式即不全是0(数值0),也不全为1(单精度数值为255,双精度数值为2047)时,都属于这类情况。在这种情况下,阶码字段被解释为以偏置(biased)形式表示的有符号整数。也就是说,阶码的值是E=e-Bias,其中e是无符号数,其位表示为ek-1...e1e0,而Bias是一个等于2k-1-1(单精度是127,双精度是1023)的偏置值。由此产生指数的取值范围,对于单精度是-126~+127,而对于双精度是-1022~+1023。
小数字段frac被解释为描述小数值f,其中0<=f<1,其二进制表示为0.fn-1...f1f0,也就是二进制小数点在最高有效位的左边。尾数定义为M=1+f。有时,这种方式也叫做隐含的以1开头的表示,因此我们可以把M看成一个二进制表达式为1.fn-1fn-2...f0的数字。既然我们总是能够调整阶码E,使得尾数M在范围1<=M<2之中,那么这种表示方法是一种轻松获得额外精度位的技巧。既然第一位总是等于1,那么我们就不需要显示地表示它。
情况2:非规格化的值
当阶码域为全0时,所表示的数是非规格化形式。在这种情况下,阶码值是E=1-Bias,而尾数的值是M=f,也就是小数字段的值,不包含隐含的开头的1。
非规格化数有两个用途。首先,它们提供了一种表示数值0的方法,因为使用规格化数,我们必须总是使M>=1,因此我们就不能表示0。实际上,+0.0的浮点表示的位模式为全0;符号位是0,阶码字段全是0(表明是一个非规格化值),而小数域也全是0,这就是得到M=f=0。令人奇怪的是,当符号位位1,而其他域全是0时,我们得到值-0.0。根据IEEE的浮点格式,值+0.0和-0.0在某些方面被认为是不同的,而在其他方面是相同的。
非规格化的另外一个功能是表示那些非常接近于0.0的数。它们提供一种熟悉,称为逐渐溢出,其中,可能的数值分布均匀的接近于0.0。
情况3:特殊值
最后一类数值时当指阶码全为1的时候出现的。当小数域全为0时,得到的值表示无穷,当s=0时是+![]() ,或者当s=1时是-
,或者当s=1时是-![]() 。当我们把两个非常大的数相乘,或者除以0时,无穷能够表示溢出的结果。当小数域为非零时,结果值被称为"NaN",(Not aNumber)。一些运算的结果不能是实数或无穷,就会返回这样的NaN值,比如计算
。当我们把两个非常大的数相乘,或者除以0时,无穷能够表示溢出的结果。当小数域为非零时,结果值被称为"NaN",(Not aNumber)。一些运算的结果不能是实数或无穷,就会返回这样的NaN值,比如计算![]() 。在某些应用中,表示未初始化的数据是,还是很有用处的。
。在某些应用中,表示未初始化的数据是,还是很有用处的。
2.4.3 数字示例
图示展示了一组数值,它们可以用假定的6位格式来表示,有k=3的阶码位和n=2的尾数位。偏置量是23-1-1=3。图示a部分显示了所有可表示的值(除了NaN)。两个无穷值在两个末端。最大数量值的规格化数![]() 14。非规格化数聚集在0的附近。图的b部分中,我们只展示了介于-1.0~+1.0之间的数值,这样就能看得更清楚了。两个零是特殊的非规格化数。可以观察到,那些可表示的数并不是均匀分布的--越靠近原点处它们越稠密。
14。非规格化数聚集在0的附近。图的b部分中,我们只展示了介于-1.0~+1.0之间的数值,这样就能看得更清楚了。两个零是特殊的非规格化数。可以观察到,那些可表示的数并不是均匀分布的--越靠近原点处它们越稠密。

图示展示了假定的8位浮点格式的示例,其中有k=4的阶码位和n=3的小数位。偏置量是24-1-1=7。图被分成了三个区域,来描述三类数字。不同的列给出了阶码字段是如何编码阶码E的,小数字段是如何编码尾数M的,以及它们一起是如何形成要表示的值V=2E*M的。从0自身开始,最靠近0的是非规格化数。这种格式的非规格化数的E=1-7=-6,得到权2E=1/64。小数f的值范围是0,1/8,...,7/8,从而得到数V的范围是0~1/64*7/8=7/512。
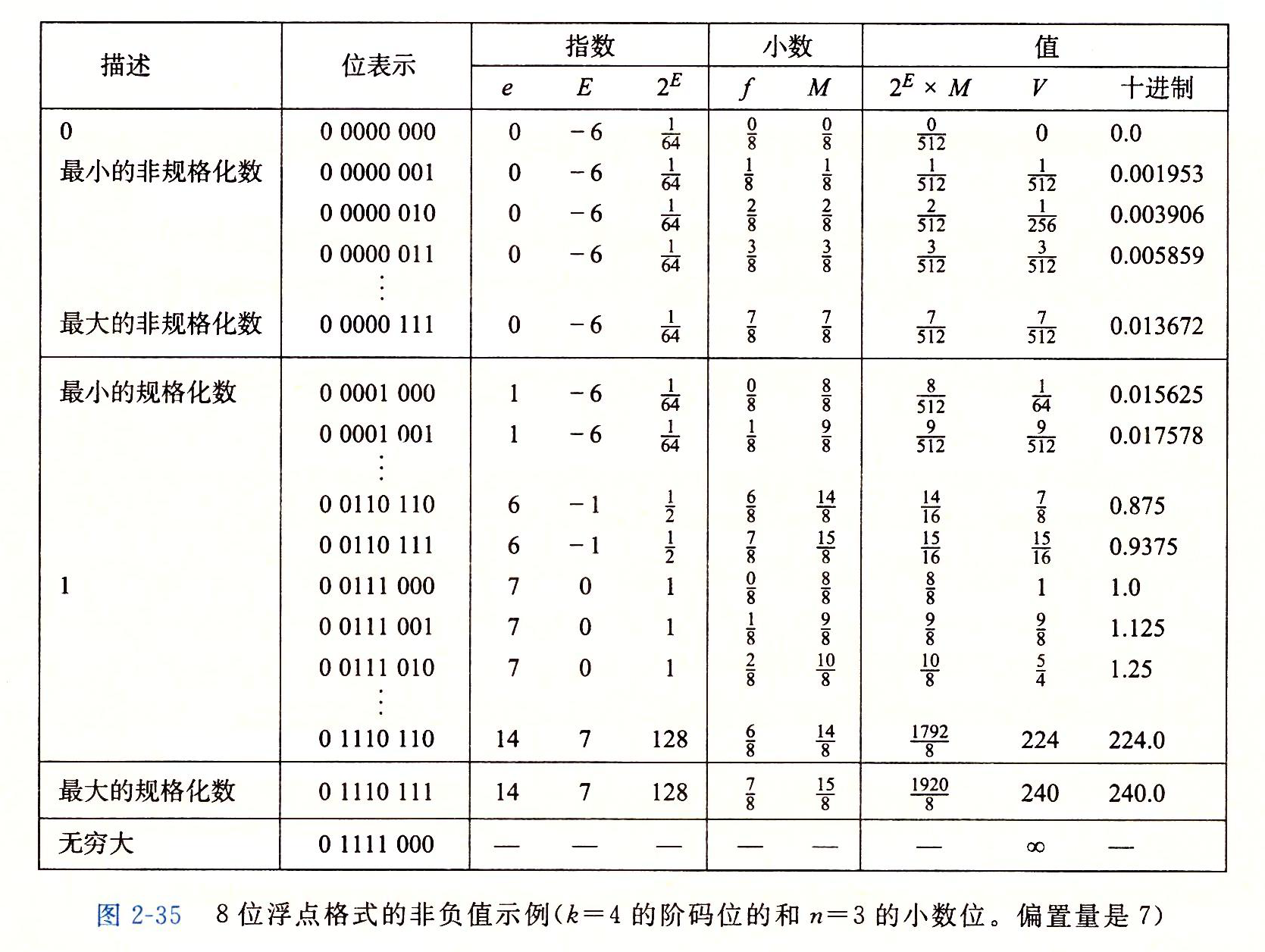
这种形式的最小规格化数同样有E=1-7=-6,并且小数取值范围也是0,1/8,...7/8。然而,尾数在范围1+0=1和1+7/8=15/8之间,得出数V在范围8/512=1/16和15/512之间。
可以观察到最大非规格化数7/512和最小非规格化数8/512之间的平滑转变。这种平滑性归功于我们对非规格化数的E的定义。通过将E定义为1-Bias,而不是-Bias,我们可以补偿非规格化数的尾数没有隐含的开头1。
当增大阶码时,我们成功地得到更大的规格化值,通过1.0后得到最大的规格化数。这个数具有阶码E=7,得到一个权2E=128。小数等于7/8得到尾数M=15/8。因此,数值是V=240。超过这个值就会 溢出到+![]() 。
。
图示展示了一些重要的单精度和双精度浮点数的表示和数字值。 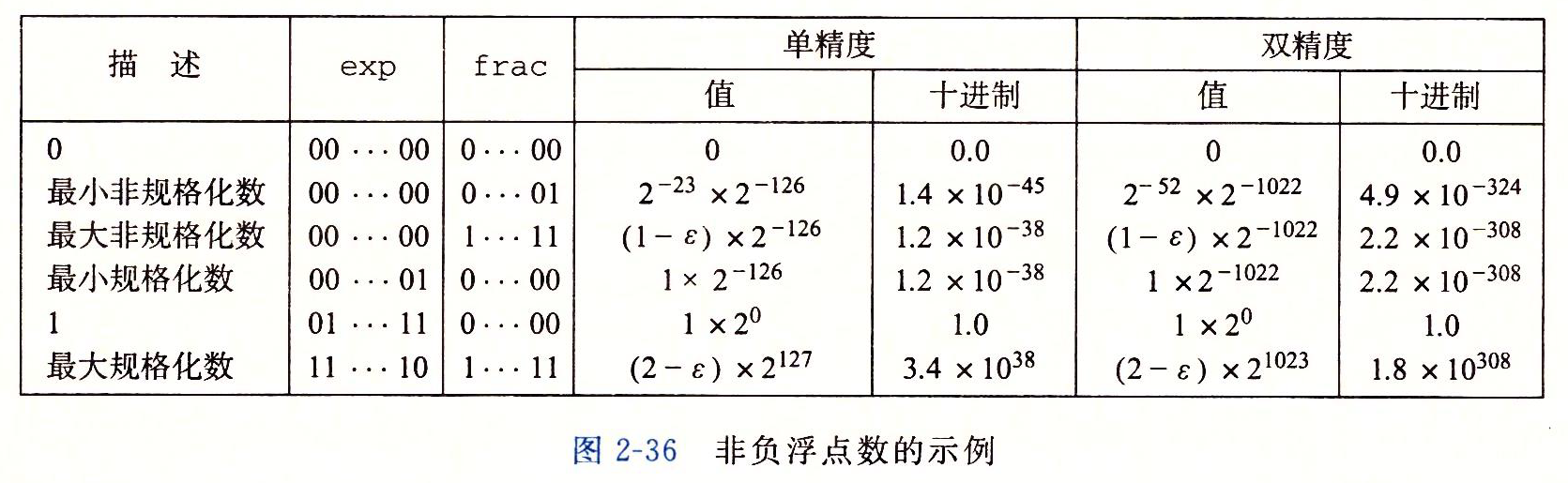
- 值+0.0 总有一个全为0的位表示。
- 最小的正非规格化值的位表示,是由最低有效位为1而其他所有位为0构成的。它具有小数(和尾数)值M=f=2-n和阶码值E=-2k-1+2。因此它的数字值是
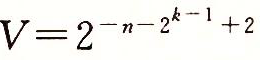
- 最大的非规格化值的位模式是由全为0的阶码字段和全为1的小数字段组成的。它有小数(和尾数)值M=f=1-2-n(我们写成1-
 )和阶码值E=-2k-1+2。因此,数值
)和阶码值E=-2k-1+2。因此,数值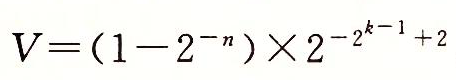 ,这仅比最小的规格化值小一点。
,这仅比最小的规格化值小一点。 - 最小的正规格化值的位模式的阶码字段的最低有效位位1,其他位全为0。它的尾数值M=1,而阶码值E=-2k-1+2。因此,数值
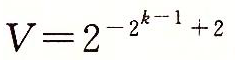
- 值1.0
- 最大的规格化值的位表示的符号位为0,阶码的最低有效位等于0,其他位等于1。它的小数值f=1-2-n,尾数M=2-2-n(写作2-
 )。它的阶码值E=2k-1-1,得到数值
)。它的阶码值E=2k-1-1,得到数值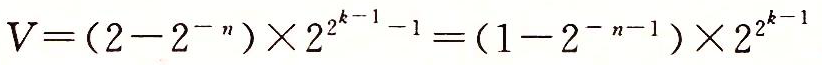 。
。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号