朴素Dijkstra

 

 

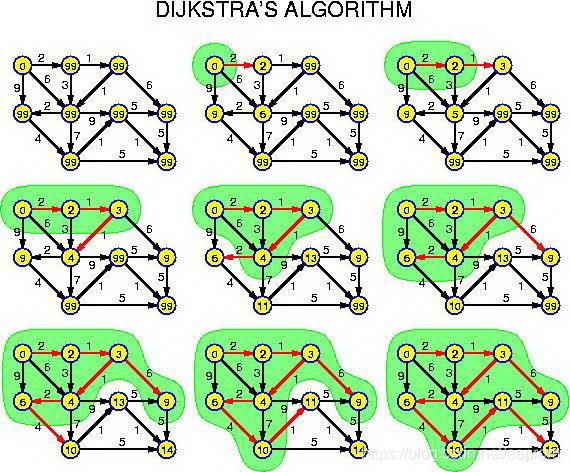
Dijkstra算法的思想是：设置两个顶点的集合S和U，集合S中存放已找到最短路径的顶点，集合U中存放当前还未找到最短路径的顶点。初始状态时，集合S中只包含源点，设为v0，然后从集合U中选择到源点v0路径长度最短的顶点u加入到集合S中，集合S中每加入一个新的顶点u都要修改源点v0到集合U中剩余顶点的当前最短路径长度值，集合U中各顶点的新的当前最短路径长度值，为原来的当前最短路径长度值与从源点过顶点u到达该顶点的路径长度中的较小者。此过程不断重复，直到集合U中的顶点全部加入到集合S中为止。

　　 朴素dijkstra算法就是暴力枚举n个点，每次枚举找到离本次枚举点最近的点a，然后用点a来更新所有其他点的距离（枚举所有点）

void dijkstra()
{
    memset(dis,0x3f,sizeof dis);  
    dis[1]=0;
    for(int i=0;i<n;i++)    //迭代n次
    { 
        int t=-1;     //表示还没有确定
        for(int j=1;j<=n;j++)  //遍历所有点
        //找到还没有确定的点中 距离最近的那个赋给t
            if(!st[j] && (t==-1||dis[t]>dis[j])) t=j;

        //if(t==n) break;  //提前找到可以退出
        st[t]=true;
        //用t来更新其他点的距离
        for(int j=1;j<=n;j++)
            dis[j]=min(dis[j],dis[t]+g[t][j]);
    }

}

最后dist[] 存的就是1号点到所有点的最短距离（本身到本身为0）。

一般不用这个时间复杂度太高，用堆优化版。