最优二叉树（Huffman 树）

题目

\(k\) 叉树 \(T\) 有 \(n\) 片树叶。每片树叶 \(v_i\) 的权为 \(w_i\)，深度为 \(l(v_i)\)。\(T\) 的权值为 \(W = \sum w_i\ l(v_i)\)。

求 \(W\) 的最小值。和在保证 \(W\) 最小的情况下，\(\max l(v_i)\) 的最小值。

数据范围：\(1 \le n \le 10^5\)，\(2 \le k \le 10\)，\(0 < w_i \le 10^{11}\)。

题目：[NOI2015] 荷马史诗

---

思路

请去翻《离散数学（第二版）》（屈婉玲著）P336。

为了保证 \(W\) 的值最小。每次贪心地选取权值最小的 \(k\) 个节点进行合并，得到新节点，其权值为前 \(k\) 小的节点权值和，其深度为 \(k\) 个节点的最大深度 \(+1\)。将新节点加入到队列中。重复上述步骤直到只剩一个节点为止。

\(T\) 的 权值 \(W\) 等于所有分支节点（不含叶节点）的权值和。

---

为了保证 \(\max l(v_i)\) 最小。每次合并时，在 \(w_i\) 相同的情况下，优先选择 \(l_i\) 的节点进行合并。

因为需要动态选择前 \(k\) 个最小值，所以使用堆（优先队列）进行维护，\(w_i\) 小的排在前面，\(w_i\) 相同的情况下 \(l_i\) 小的排在前面。

最大深度 \(\max l(v_i)\) 等于最后剩余的一个节点的深度。

---

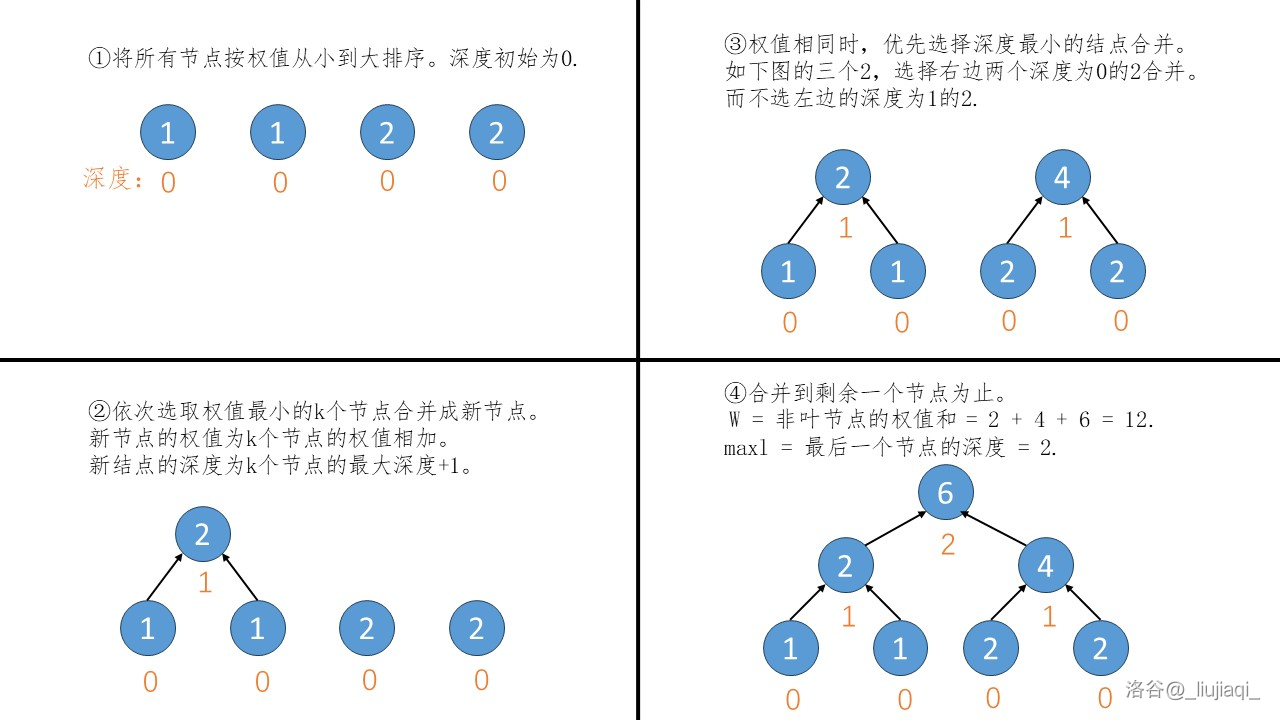
样例 #\(1\)：

4 2
1
1
2
2

---

注意

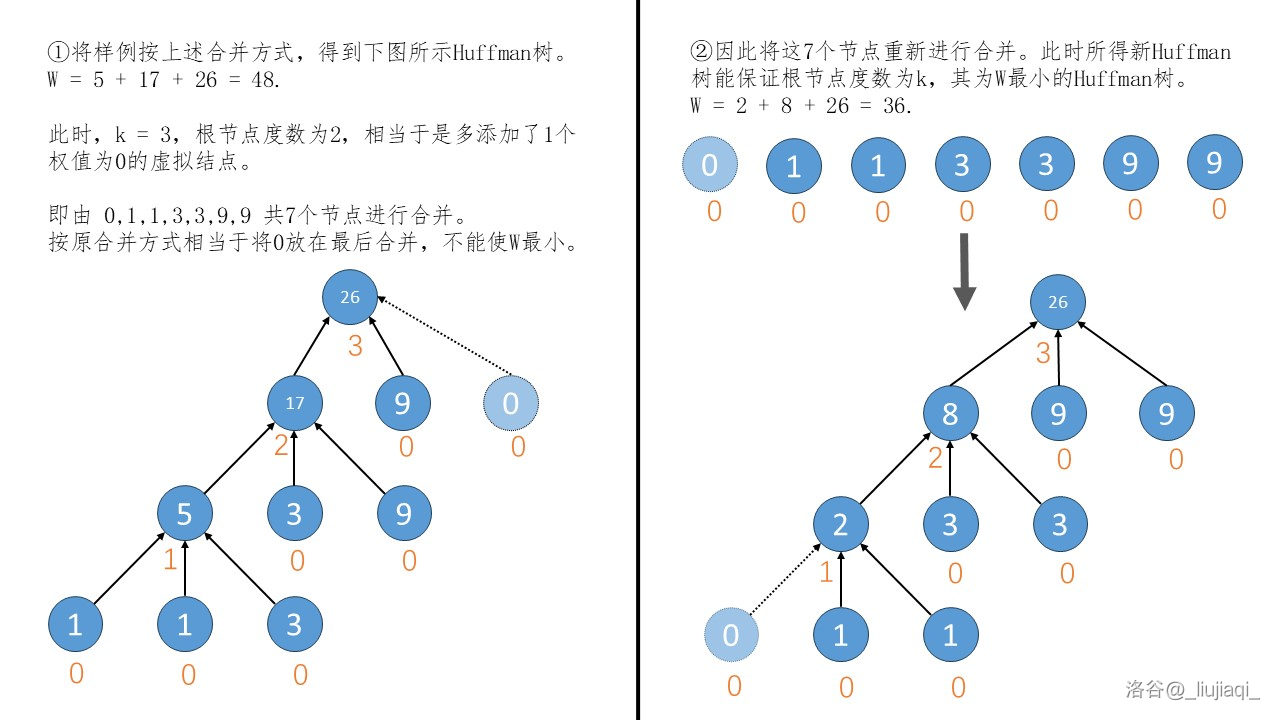
在非 \(2\) 阶 Huffman 树的情况下，最后一次合并的过程时，可能出现不足 \(k\) 个值的情况。解决办法是，添加权值为 \(0\) 的虚拟节点，以保证根节点的度数必然为 \(k\) 个。

第一次合并减少了 k 个叶节点，从第二次合并开始，每次减少 1 个新节点和 k-1 个叶节点。因此，最后一次合并时，剩余的叶节点个数为 (n-1)%(k-1)。

如果剩余叶节点个数为 \(0\)，说明能保证根节点的度数为 \(k\)。否则，应该加上 (k-1)-(n-1)%(k-1) 个虚拟节点，以保证最后一次合并时一共有 k-1 个叶节点。

---

样例 #\(2\)：

6 3
1
1
3
3
9
9

---

需要注意一点。数据范围是 \(0 < w_i \le 10^{11}\)，因此需要开 \(long \; long\)。

十年 OI 一场空，忘开 long long 见祖宗。

---

代码

#include <queue>
#include <cstdio>
#define int long long
struct Node {
    int w, l;
    // w 为权值 w[i]，l 为深度 (高度) l[i]。
    bool operator < (const Node &b) const {
        return w == b.w ? l > b.l : w > b.w;
        // 重载小于号。STL 的优先队列为大根堆，所以用大于号。
        // 优先按权值 w 从小到大排序，w 相等时 按照深度 l 从小到大排序。
    }
};
std::priority_queue <Node> q;
// 选取前 k 个最小值，用优先队列进行维护。
int max(int x, int y) {
    return x > y ? x : y;
}
signed main() {
    int n, k, x;
    scanf("%lld%lld", &n, &k);
    for (int i = 1; i <= n; ++i) {
        scanf("%lld", &x);
        q.push((Node) {x, 0});
        // 把所有叶节点加入队列中，初始深度都为 0。
    }
    x = (k - 1 - (n - 1) % (k - 1)) % (k - 1);
    for (int i = 1; i <= x; ++i) {
        q.push((Node) {0, 0});
        // 加入虚拟节点。
    }
    int W = 0, maxl = 0;
    // W 为 Huffman 树的权值，maxl 为最大深度。
    while (!q.empty()) {
        Node d = (Node) {0, 0};
        for (int i = 1; i <= k; ++i) {
            Node x = q.top(); q.pop();
            d.w += x.w;
            d.l = max(d.l, x.l + 1);
            // 取出前 k 个节点，合并为 1 个新节点。
            // 新节点的权值为各个叶节点权值相加，新节点的深度为最深的叶节点的深度 + 1。
        }
        W += d.w;
        maxl = max(maxl, d.l);
        // W 等于非叶节点的节点权值和。
        // maxl 为所有节点的最深深度 + 1。
        if (!q.empty()) q.push(d);
        // 如果只剩最后一个新节点，且没有叶节点时，跳出循环。
    }
    printf("%lld\n%lld\n", W, maxl);
    return 0;
}