【説明する】グラフ理論
数组模拟邻接表存储
详细请见:http://www.cnblogs.com/zxqxwnngztxx/p/6682624.html
图的遍历
遍历是很多图论算法的基础,所谓图的遍历( graph traversal),也称为搜索( search),就是从图中某个顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访问一次。

1)DFS 遍历
DFS( 顶点 u ) { //从顶点 i 进行深度优先搜索
vis[ u ] = 1; //将顶点 i 的访问标志置为 1
for( j=1; j<=n; j++ ) { //对其他所有顶点 j
//j 是 i 的邻接顶点,且顶点 j 没有访问过
if( map[u][ j ]==1 && !vis[ j ] ) {
//递归搜索前的准备工作需要在这里写代码
DFS( j ) //从顶点 j 出发进行 DFS 搜索
//以下是 DFS 的回退位置
//在很多应用中需要在这里写代码
}
}
}
(2)BFS 遍历


1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 6 using namespace std; 7 const int Maxn=1010; 8 9 /* 10 样例 11 9 10 12 A B 13 A D 14 A E 15 B C 16 B E 17 C G 18 D F 19 E F 20 F H 21 H I 22 */ 23 24 int m,n; 25 int g[Maxn][Maxn],que[Maxn]; 26 bool d[Maxn]; 27 bool b[Maxn]; 28 29 void dfs(int i)//递归 30 { 31 if(i<n-1) cout<<char(i+64)<<"-->"; 32 else cout<<char(i+64);//防止最后多输出一个箭头 33 d[i]=1; //进行标记已经被搜过 34 for(int k=1;k<=n;k++) 35 { 36 if(g[i][k]==1&&!d[k])//如果k为是 i 的邻接顶点并且k没有被搜过 37 { 38 dfs(k);//继续搜索k 39 } 40 } 41 } 42 43 44 void bfs(int u)//非递归 45 { 46 b[u]=1;//将第一个元素进行标记 47 cout<<(char)(u+64);//并输出 48 int head=0,tail=1;//制定队头与队尾 49 que[1]=u;//将第一个元素进队列,作为头号元素 50 while(head<tail)//当队头队尾重合之前 51 { 52 head++;//删除第一个元素,将head指针指向下一个 53 for(int i=1;i<=n;i++) 54 { 55 if(g[que[head]][i]==1&&!b[i])//如果为此时搜索的邻接顶点并且为被标记 56 { 57 b[i]=1; 58 que[++tail]=i;//入队 59 } 60 } 61 } 62 } 63 64 int main() 65 { 66 char a,b; 67 scanf("%d %d",&m,&n); 68 for(int i=1;i<=n;i++) 69 { 70 cin>>a>>b;//需要用cin输入 71 g[a-64][b-64]=g[b-64][a-64]=1;//进行标记 72 } 73 printf("dfs\n"); 74 dfs(1); 75 printf("\n"); 76 memset(que,0,sizeof(que)); 77 printf("bfs\n"); 78 bfs(1); 79 for(int i=2;i<n;i++) 80 { 81 cout<<"-->"<<(char)(que[i]+64);//输出队列 82 } 83 return 0; 84 }
求最短路的3种算法
1)Floyed算法 O(N3)
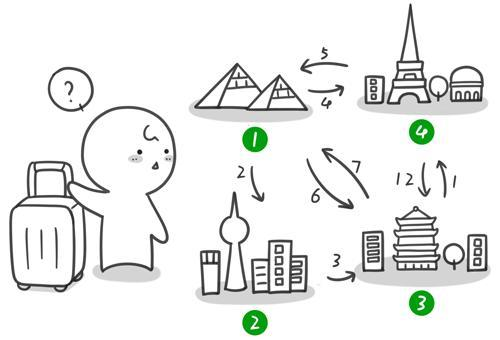
暑假,小哼准备去一些城市旅游。有些城市之间有公路,有些城市之间则没有,如下图。为了节省经费以及方便计划旅程,小哼希望在出发之前知道任意两个城市之前的最短路程。
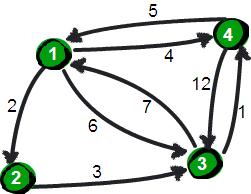
上图中有4个城市8条公路,公路上的数字表示这条公路的长短。
请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。
详细过程请见:直通

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define Maxn 1001 5 6 using namespace std; 7 8 int maps[Maxn][Maxn]; 9 int ans; 10 11 int main() 12 { 13 memset(maps,999999,sizeof(maps)); 14 int n,m; 15 cin>>n>>m; 16 int he,ta,len; 17 for(int i=1; i<=m; i++) 18 { 19 cin>>he>>ta>>len; 20 maps[ta][he]=maps[he][ta]=len; 21 } 22 int x,y; 23 cin>>x>>y; 24 for(int k = 1; k <= n; k++) 25 for(int i = 1; i <= n; i++) 26 for(int j = 1; j <= n; j++) 27 { 28 if(maps[i][j]>maps[i][k]+maps[k][j]) 29 maps[i][j]=maps[i][k]+maps[k][j]; //进行更新 30 } 31 32 printf("%d",maps[x][y]); 33 return 0; 34 }
2)Dijkstra算法O (N2)

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 5 using namespace std; 6 7 const int Maxn=0x7f,mm=1001; 8 int map[mm][mm]; //输入关系 9 int minn; //the最小值 10 int n,m,s1,ss,k; //度and起止点 11 int dis[mm]; //统计关系 12 int p[mm]; //进行输出关系 13 bool b[mm]; 14 15 void print(int u,int v) 16 {//如果需要输出如何到达 17 int que[mm]; 18 int tot=1; 19 que[tot]=v; 20 tot++; 21 int temp=p[v]; 22 while(temp!=u) 23 { 24 que[tot]=temp; 25 tot++; 26 temp=p[temp]; 27 } 28 que[tot]=u; 29 for(int i=tot;i>=1;i--) 30 if(i!=1) 31 cout<<que[i]<<"-->"; 32 else 33 cout<<que[i]<<endl; 34 } 35 36 void Dijkstra(int s) 37 { 38 for(int i=1; i<=n; i++) 39 { 40 dis[i]=map[s][i]; 41 if(dis[i]!=Maxn) 42 p[i]=s; //指向s 43 else 44 p[i]=0; //不进行指向 45 } 46 b[s]=1; 47 dis[s]=0; 48 for(int i=1; i<=n-1; i++) 49 { 50 minn=Maxn; //便于寻找 51 k=s; //起点 52 for(int j=1; j<=n; j++) 53 if(!b[j]&&dis[j]<minn) 54 { 55 minn=dis[j]; //寻找最小值 56 k=j; //用k进行记录最小值 57 } 58 b[k]=1; //进行标记 59 for(int q=1; q<=n; q++) 60 if(!b[q]&&dis[q]>dis[k]+map[k][q]&&map[k][q]<Maxn) { 61 dis[q]=dis[k]+map[k][q]; 62 p[q]=k; 63 } 64 } 65 } 66 67 void gett() 68 { 69 int x,y,w; 70 for(int i=1; i<=m; i++) 71 { 72 cin>>x>>y>>w; 73 map[x][y]=map[y][x]=w; 74 } 75 } 76 77 int main() 78 { 79 scanf("%d %d",&n,&m); 80 memset(map,Maxn,sizeof(map)); 81 gett(); 82 memset(dis,Maxn,sizeof(dis)); 83 scanf("%d %d",&s1,&ss); 84 Dijkstra(s1); 85 printf("%d\n",dis[ss]);//仅输出最短路线的长度即可 86 print(s1,ss); 87 return 0; 88 }
3)SPFA算法O(kE)

样例:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 5 using namespace std; 6 const int Maxn=1001,Maxx=999999; 7 8 int que[Maxn],map[Maxn][Maxn],dis[Maxn]; 9 bool cun[Maxn]; 10 int n,m; 11 int qianqu[Maxn],q[Maxn]; 12 13 void SPFA(int s) 14 { 15 int head=0,tail=1,v; 16 que[1]=s; //将s入队 17 dis[s]=0; //s to s 的距离为0 18 qianqu[s]=s; //记录下s的前驱 19 cun[s]=1; //进行标记,已经入队 20 do 21 { 22 v=que[++head]; //取出队头元素 23 cun[v]=0; //将标记撤销,说明已经出队 24 for(int i=1;i<=n;i++) 25 { 26 if(dis[i]>dis[v]+map[v][i]) //进行松弛 27 { 28 dis[i]=dis[v]+map[v][i]; 29 qianqu[i]=v; //记录前驱 30 if(!cun[i]) //如果队中没有i元素 31 { 32 que[++tail]=i; //入队 33 cun[i]=1; //进行标记,已经入队 34 } 35 } 36 } 37 38 }while(head<tail); //进行循环的条件 39 } 40 41 void print(int s,int e) 42 { 43 int tot=1; 44 q[tot]=e; 45 tot++; 46 int temp=qianqu[e]; 47 while(temp!=s) 48 { 49 q[tot]=temp; 50 tot++; 51 temp=qianqu[temp]; 52 } 53 q[tot]=s; 54 for(int i=tot;i>=1;i--) 55 { 56 if(i!=1) 57 cout<<q[i]<<"-->"; 58 else 59 cout<<q[i]<<endl; 60 } 61 } 62 63 int main() 64 { 65 memset(dis,Maxx,sizeof(dis)); //dis与map必须!!!进行初始化 66 memset(map,Maxx,sizeof(map)); //这样才能够松弛 67 scanf("%d %d",&n,&m); 68 int q,h,w,s,e; 69 for(int i=1;i<=m;i++) 70 { 71 scanf("%d %d %d",&q,&h,&w); 72 map[q][h]=w; 73 } 74 //memset(cun,0,sizeof(cun)); 75 //memset(que,0,sizeof(que)); 76 //这两个可以不用进行初始化 77 scanf("%d %d",&s,&e); 78 SPFA(s); 79 printf("%d\n",dis[e]); 80 print(s,e); 81 return 0; 82 }
超详细讲解——
orz http://www.cnblogs.com/mjtcn/p/7599217.html
tarjan算法
tarjan算法,一个关于 图的联通性的神奇算法。基于DFS算法,深度优先搜索一张有向图。!注意!是有向图。根据树,堆栈,打标记等种种神奇方法来完成剖析一个图的工作。而图的联通性,就是任督二脉通不通。。的问题。
了解tarjan算法之前你需要知道:
强连通,强连通图,强连通分量,解答树(解答树只是一种形式。了解即可)
强连通(strongly connected):
在一个有向图G里,设两个点 a b 发现,由a有一条路可以走到b,由b又有一条路可以走到a,我们就叫这两个顶点(a,b)强连通。
强连通图:
如果 在一个有向图G中,每两个点都强连通,我们就叫这个图,强连通图。
强连通分量strongly connected components):
在一个有向图G中,有一个子图,这个子图每2个点都满足强连通,我们就叫这个子图叫做强连通分量[分量::把一个向量分解成几个方向的向量的和,那些方向上的向量就叫做该向量(未分解前的向量)的分量]
举个简单的栗子:

比如说这个图,在这个图中呢,点1与点2互相都有路径到达对方,所以它们强连通.
而在这个有向图中,点1 2 3组成的这个子图,是整个有向图中的强连通分量。
解答树:
就是一个可以来表达出递归枚举的方式的树(图),其实也可以说是递归图。。反正都是一个作用,一个展示从“什么都没有做”开始到“所有结求出来”逐步完成的过程。“过程!”
tarjan算法,之所以用DFS就是因为它将每一个强连通分量作为搜索树上的一个子树。而这个图,就是一个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进行。每个点都有两个参数。
1, DFN[]作为这个点搜索的次序编号(时间戳),简单来说就是 第几个被搜索到的。%每个点的时间戳都不一样%。
2, LOW[]作为每个点在这颗树中的,最小的子树的根,每次保证最小,喜欢它的父亲结点的时间戳这种感觉。如果它自己的LOW[]最小,那这个点就应该从新分配,变成这个强连通分量子树的根节点。
ps:每次找到一个新点,这个点LOW[]=DFN[]。
而为了存储整个强连通分量,这里挑选的容器是,堆栈。每次一个新节点出现,就进栈,如果这个点有 出度 就继续往下找。直到找到底,每次返回上来都看一看子节点与这个节点的LOW值,谁小就取谁,保证最小的子树根。如果找到DFN[]==LOW[]就说明这个节点是这个强连通分量的根节点(毕竟这个LOW[]值是这个强连通分量里最小的。)最后找到强连通分量的节点后,就将这个栈里,比此节点后进来的节点全部出栈,它们就组成一个全新的强连通分量。
先来一段伪代码:
tarjan(u) { DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值 Stack.push(u) // 将节点u压入栈中 for each (u, v) in E // 枚举每一条边 if (v is not visted) // 如果节点v未被访问过 tarjan(v) // 继续向下找 Low[u] = min(Low[u], Low[v]) else if (v in S) // 如果节点u还在栈内 Low[u] = min(Low[u], DFN[v]) if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根 repeat v = S.pop // 将v退栈,为该强连通分量中一个顶点 print v until (u== v) }
来一发裸代码!
输入:
一个图有向图。
输出:
它每个强连通分量。
input:
6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6
output:
6
5
3 4 2 1
代码酱=u=

#include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int M = 1001; struct node { int v,next; } edge[M]; int DFN[M],LOW[M]; int stack[M],heads[M],visit[M]; int cnt,tot,index; void add(int x,int y) { edge[++cnt].next=heads[x]; edge[cnt].v = y; heads[x]=cnt; return ; } void tarjan(int x)///代表第几个点在处理.递归的是点. { DFN[x]=LOW[x]=++tot;///新进点的初始化. stack[++index]=x;///进栈 visit[x]=1;///表示在栈里 for(int i=heads[x]; i!=-1; i=edge[i].next) { if(!DFN[edge[i].v]) { ///如果没访问过 tarjan(edge[i].v);///往下进行延伸,开始递归 LOW[x]=min(LOW[x],LOW[edge[i].v]);///递归出来,比较谁是谁的儿子/父亲,就是树的对应关系,涉及到强连通分量子树最小根的事情。 } else if(visit[edge[i].v ]) { ///如果访问过,并且还在栈里. LOW[x]=min(LOW[x],DFN[edge[i].v]);///比较谁是谁的儿子/父亲.(就是链接对应关系) } } if(LOW[x]==DFN[x]) ///发现是整个强连通分量子树里的最小根. { Do { printf("%d ",stack[index]); visit[stack[index]]=0; index--; }while(x!=stack[index+1]); //出栈,并且输出。 printf("\n"); } return ; } int main() { memset(heads,-1,sizeof(heads)); int n,m; scanf("%d%d",&n,&m); int x,y; for(int i=1; i<=m; i++) { scanf("%d%d",&x,&y); add(x,y); } for(int i=1; i<=n; i++) if(!DFN[i]) tarjan(i);///当这个点没有访问过,就从此点开始。防止图没走完 return 0; }
最小生成树
(注:给出2种代码均可以ACluoguP3366题)题解
最小生成树的简单定义
给定一股无向联通带权图G(V,E).E 中的每一条边(v,w)权值位C(v,w)。
如果G的子图G'是一个包含G中所有定点的子图,那么G'称为G的生成树,如果G'的边的权值最小那么G'称为G的最小生成树。
1)Prim(普里姆)算法(采用贪心)
from http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html
(可能外加自己的理解?)
1.引入
图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点
2.算法简单描述
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
下面对算法的图例描述
| 图例 | 说明 | 不可选 | 可选 | 已选(Vnew) |
|---|---|---|---|---|
|
|
此为原始的加权连通图。每条边一侧的数字代表其权值。 | - | - | - |
|
|
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示。 | C, G | A, B, E, F | D |
|
|
下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示。 | C, G | B, E, F | A, D |
 |
算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。 | C | B, E, G | A, D, F |
|
|
在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。E最近,因此将顶点E与相应边BE高亮表示。 | 无 | C, E, G | A, D, F, B |
|
|
这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C,并与边EC一同高亮表示。 | 无 | C, G | A, D, F, B, E |
|
|
顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故高亮表示G及相应边EG。 | 无 | G | A, D, F, B, E, C |
|
|
现在,所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。 | 无 | 无 | A, D, F, B, E, C, G |
3.简单证明prim算法
反证法:假设prim生成的不是最小生成树
1).设prim生成的树为G0
2).假设存在Gmin使得cost(Gmin)<cost(G0) 则在Gmin中存在<u,v>不属于G0
3).将<u,v>加入G0中可得一个环,且<u,v>不是该环的最长边(这是因为<u,v>∈Gmin)
4).这与prim每次生成最短边矛盾
5).故假设不成立,命题得证.
4.c++代码实现

#include <iostream> #include <cstdio> #define Maxx 0x7fffffff using namespace std; const int M = 5050; int n,m; //n=顶点的个数,m=边的个数 int edge[M][M]={ /*输入的邻接矩阵*/ }; int lowcost[M]; //记录Vnew中每个点到V中邻接点的最短边 bool visited[M]; //标记某点是否加入Vnew int pre[M]; //记录V中与Vnew最邻近的点 void prim(int start) { int sumweight=0,i,j,k=0; visited[start]=true; for(i=1;i<=n;i++) { lowcost[i]=edge[start][i]; pre[i]=start; } int minn=Maxx; //最小权值 int v=-1; //所对应的下标 for(i=1;i<n;i++) //进行n-1次,因为此时已经知道当前start点到另一点距离最短 { minn=Maxx; for(j=1;j<=n;j++) { if(visited[j]==false && lowcost[j]<minn) //在Vnew之外寻找最短路径 { minn=lowcost[j]; //最短路径 v=j; } } // printf("%d %d %d\n",pre[v],v,lowcost[v]); if(v==-1) { cout<<"orz"<<endl; return; } visited[v]=true; //将v加Vnew中 sumweight+=lowcost[v]; //计算路径长度之和 for(j=1;j<=n;j++) { if(visited[j]==false && edge[v][j]<lowcost[j]) { lowcost[j]=edge[v][j]; //此时v点加入Vnew 需要更新lowcost pre[j]=v; } } } // printf("the minmum weight is %d",sumweight); //进行输出 printf("%d",sumweight); } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) { // lowcost[i]=Maxx; for(int j=1; j<=n; j++) edge[i][j]=Maxx; //初始化图 } int x,y,w,s,Max=Maxx; for(int k=1; k<=m; k++) { cin>>x>>y>>w; if(w<edge[x][y]) edge[x][y]=edge[y][x]=w; //构建图 if(w<Max) { Max=w; s=x; //寻找最初最"实惠"的点 } } prim(s); //进行求解最小生成树 return 0; }
5.时间复杂度
这里记顶点数v,边数e
邻接矩阵:O(v2) 邻接表:O(elog2v)
2)Kruskal(克鲁斯卡尔)算法(采用并查集)
用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。和Boruvka算法不同的地方是,Kruskal算法在图中存在相同权值的边时也有效。
(所有的边从短到长进行排序,每次都选取最短的边)
1.kruskal算法的基本思想:
1.首先将G的n个顶点看成n个孤立的连通分支(n个孤立点)并将所有的边按权从小大排序。
2.按照边权值递增顺序,如果加入边后存在圈则这条边不加,直到形成连通图
对2的解释:如果加入边的两个端点位于不同的连通支,那么这条边可以顺利加入而不会形成圈
2.算法简单描述
1).记Graph中有v个顶点,e个边
2).新建图Graphnew,Graphnew中拥有原图中相同的e个顶点,但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环:从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中
if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中
添加这条边到图Graphnew中
图例描述:
首先第一步,我们有一张图Graph,有若干点和边,如右图: 
然后将所有的边的长度排序,用排序的结果作为我们选择边的依据,这里再次体现了贪心算法的思想。
资源排序,对局部最优的资源进行选择,排序完成后,我们率先选择了边AD。这样我们的图就变成了右图:
在剩下的边中寻找,我们找到了CE,这里边的权重也是5,如右:
依次类推我们找到了6,7,7,即DF,AB,BE,如右:
下面继续选择, BC或者EF尽管现在长度为8的边是最小的未选择的边。
但是现在他们已经连通了(对于BC可以通过CE,EB来连接,类似的EF可以通过EB,BA,AD,DF来接连),所以不需要选择他们。
类似的BD也已经连通了(这里上图的连通线用红色表示了)。

3.简单证明Kruskal算法
对图的顶点数n做归纳,证明Kruskal算法对任意n阶图适用。
归纳基础:
n=1,显然能够找到最小生成树。
归纳过程:
假设Kruskal算法对n≤k阶图适用,那么,在k+1阶图G中,我们把最短边的两个端点a和b做一个合并操作,
即把u与v合为一个点v',把原来接在u和v的边都接到v'上去,这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边),G'最小生成树T'可以用Kruskal算法得到。
我们证明T'+{<u,v>}是G的最小生成树。
用反证法,如果T'+{<u,v>}不是最小生成树,最小生成树是T,即W(T)<W(T'+{<u,v>})。
显然T应该包含<u,v>,否则,可以用<u,v>加入到T中,形成一个环,删除环上原有的任意一条边,形成一棵更小权值的生成树。
而T-{<u,v>},是G'的生成树。所以W(T-{<u,v>})<=W(T'),也就是W(T)<=W(T')+W(<u,v>)=W(T'+{<u,v>}),产生了矛盾。
于是假设不成立,T'+{<u,v>}是G的最小生成树,Kruskal算法对k+1阶图也适用。
由数学归纳法,Kruskal算法得证。
4.c++代码实现

#include <algorithm> #include <iostream> #include <cstdio> using namespace std; const int N = 5010; const int M = 200020; int n,m,ans; int dad[N]; struct A { int u,v,w; bool operator < (const A &qwq)const { return w < qwq.w; } }t[M]; int getdad(int x) { return dad[x] == x ? x : dad[x] = getdad( dad[x] ); } void kruskal() { sort(t+1,t+1+m); for(int i=1;i<=m;i++) { int f1=getdad(t[i].u),f2=getdad(t[i].v); if(f1!=f2) { dad[f1]=f2; ans+=t[i].w; } } int tmp=getdad(1); for(int i=2;i<=n;i++) { if(getdad(i)!=tmp) { printf("orz"); return; } } printf("%d\n",ans); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) scanf("%d%d%d",&t[i].u,&t[i].v,&t[i].w); for(int i=1;i<=n;i++) dad[i]=i; kruskal(); return 0; }
5.时间复杂度:
elog2e e为图中的边数










 浙公网安备 33010602011771号
浙公网安备 33010602011771号