1 #include<iostream>
2 #include<cmath>
3 #include<cstdio>
4 #include<iomanip>
5 using namespace std;
6 double h=0.1;//步差
7 double xi[11]={0};
8 double ol_yi[11]={1};
9 double gol_yi[11]={1};
10 double rk_yi[11]={1};
11 double real_yi[11]={1};
12 double f(double x,double y){
13 return 2*x/(3*y*y);
14 }//f(x,y)
15 void OLFunction(){
16 for(int i=0;i<10;i++){
17 ol_yi[i+1]=ol_yi[i]+h*f(xi[i],ol_yi[i]);
18 }
19 }//欧拉方法
20 void GOLFunction(){
21 for(int i=0;i<10;i++){
22 gol_yi[i+1]=gol_yi[i]+
23 h*(
24 f(xi[i],gol_yi[i])
25 +f(xi[i+1],gol_yi[i]+h*f(xi[i],gol_yi[i]))
26 )/2;
27 }
28 }//改进欧拉方法
29 void RKFunction(){
30 double K1,K2,K3,K4;
31 for(int i=0;i<10;i++){
32 K1=f(xi[i],rk_yi[i]);
33 K2=f(xi[i]+h/2,rk_yi[i]+h*K1/2);
34 K3=f(xi[i]+h/2,rk_yi[i]+h*K2/2);
35 K4=f(xi[i]+h,rk_yi[i]+h*K3);
36 rk_yi[i+1]=rk_yi[i]+h*(K1+2*K2+2*K3+K4)/6;
37 }
38 }//经典龙格贝法
39 void RFunction(){
40 for(int i=1;i<11;i++){
41 real_yi[i]=pow(1.0+xi[i]*xi[i],1/3.0);
42 }
43 }//真实解
44 int main(){
45 int i;
46 for(i=1;i<11;i++){
47 xi[i]=xi[i-1]+h;
48 }//求xi[]
49
50 OLFunction();//四种计算方法
51 GOLFunction();
52 RKFunction();
53 RFunction();
54
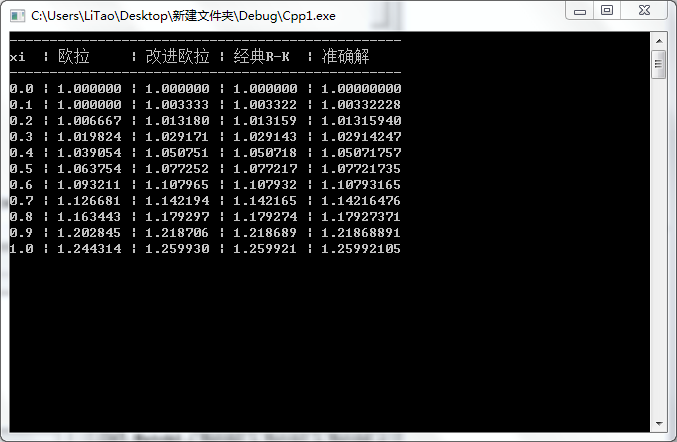
55 printf("-------------------------------------------------\n");
56 printf("xi | 欧拉 | 改进欧拉 | 经典R-K | 准确解 \n");
57 printf("-------------------------------------------------\n");
58 for(i=0;i<11;i++){
59 printf("%.1lf | %.6lf | %.6lf | %.6lf | %.8lf\n",
60 xi[i],ol_yi[i],gol_yi[i],rk_yi[i],real_yi[i]);
61 }
62 getchar();
63 return 0;
64 }
