什么是旋转矩阵
旋转矩阵描述了两个坐标系(SLAM中两个时刻机器人的姿态)之间的相互关系,是SLAM中描述姿态变换的数学工具。为了更深入地理解旋转矩阵及坐标变化,我们简单地以两个原点重合的坐标系来阐释旋转矩阵的含义及其性质。
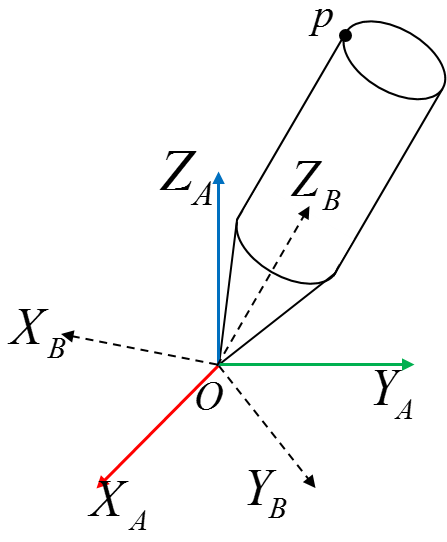
有两个坐标系:$B$,$A$,其中$B$为刚体坐标系;两坐标系原点重合,点$p$是刚体上的一点
坐标系B的坐标轴单位向量在坐标系A中的描述为:
$$
\vec X_B=\begin{bmatrix}\alpha_x \\\beta_x \\\gamma_x \\\end{bmatrix},\vec Y_B=\begin{bmatrix}\alpha_y \\\beta_y \\\gamma_y \\\end{bmatrix},\vec Z_B=\begin{bmatrix}\alpha_z \\\beta_z \\\gamma_z \\\end{bmatrix}
$$
点$p$在坐标系$B$和坐标系$A$中的坐标分别为 $p_ B$ ,$p_A$,如下
$$
p_B=\begin{bmatrix}x_B \\y_B \\z_x \\\end{bmatrix},p_A=\begin{bmatrix}x_A \\y_A \\z_A \\\end{bmatrix}
$$
这里有一个重要的理解:**坐标是基于某一个坐标系下满足一定条件的若干参考向量的度量**。点$p_B$在坐标系$B$中的坐标,其实是基于坐标系$B$中三个单位正交基$e_x=\begin{bmatrix}1&0&0\end{bmatrix}^T$,$e_y=\begin{bmatrix}0&1&0\end{bmatrix}^T$,$e_z=\begin{bmatrix}0&0&1\end{bmatrix}^T$,进行的度量,即:
$$
p_B=x_B\cdot\begin{bmatrix}1 \\0 \\0 \\\end{bmatrix}+y_B\cdot\begin{bmatrix}0 \\1 \\0 \\\end{bmatrix}+z_B\cdot\begin{bmatrix}0 \\0 \\1 \\\end{bmatrix}
$$
点$q$在坐标系$A$中的坐标$p_A$可以以坐标系$A$中三个单位正交向量$\vec X_B=\begin{bmatrix}\alpha_x&\alpha_y&\alpha_y\end{bmatrix}^T$,$\vec Y_B=\begin{bmatrix}\beta_y&\beta_y&\beta_y\end{bmatrix}^T$,$\vec Z_B=\begin{bmatrix}\gamma_z&\gamma_z&\gamma_z\end{bmatrix}^T$来进行度量,坐标分别为$x_B$,$y_B$,$z_B$,则点$p$在坐标系$A$中表达如下:
$$
\begin{align}
p_A&=x_B\cdot \vec X_B+y_B\cdot \vec Y_B+z_B\cdot \vec Z_B \\
&=x_B\cdot \begin{bmatrix}\alpha_x \\\beta_x \\\gamma_x \\\end{bmatrix}+ y_B\cdot \begin{bmatrix}\alpha_y \\\beta_y \\\gamma_y \\\end{bmatrix}+z_B\cdot \begin{bmatrix}\alpha_z \\\beta_z \\\gamma_z \\\end{bmatrix} \\
&=\begin{bmatrix}\alpha_x & \alpha_y &\alpha_z \\\beta_x & \beta_y & \beta_z \\\gamma_x & \gamma_y & \gamma_z \\\end{bmatrix}\cdot \begin{bmatrix}x_B \\y_B \\z_x \\\end{bmatrix} \\
&=R_B^A \cdot p_B
\end{align}
$$
综上:点$p$在坐标系$A$中坐标和在坐标系$B$中坐标有如下关系:
$$
p_A=R_B^A\cdot p_B
$$
$R_B^A$为旋转矩阵:是坐标系$A$到坐标系$B$的旋转矩阵,也是坐标系$B$在坐标系$A$中的描述(即刚体在坐标系$A$中的姿态)
上述结论成立的条件:坐标系$A$与坐标系$B$的原点相同
关于旋转矩阵作用的直观理解:
$$
p_A(在A中坐标)=R_B^A(B在A中的描述)\cdot p_B(在B中坐标)
$$
这是对旋转矩阵作用比较本质的理解,在后续**IMU标定**相关的博客中会用到这一理解
### 旋转矩阵的性质
- **旋转矩阵的合成法则**:两个坐标系之间的旋转矩阵可以利用它们与中间坐标系间的旋转矩阵相乘得到,该结论可以拓展到多个矩阵
$$
R_C^A=R_B^A\cdot R_C^B
$$
- **性质1**
设$R$是旋转矩阵,$r_1$ ,$r_2$ ,$r_3$ 是其列向量,则它们是相互正交的,即:
$$
r_i^Tr_j=\begin{cases}0 &i\neq j \\ 1 &i=j \end{cases}
$$
- **性质2**
设 R是旋转矩阵,则有:
$$
RR^T=R^TR=I
$$
- **性质3**
$$
detR=1
$$
满足上述性质的3×3矩阵的集合定义为**特殊正交群$SO(3)$:**(**群** 的概念后面会介绍到)
$$
SO(3)=\{R\in \mathcal R^{3×3}|RR^T=I,det R = 1\}
$$
变换矩阵与齐次坐标
如上图,有两个坐标系:$B$,$A$,其中$B$为刚体坐标系;$B$坐标系原点在$A$坐标系中的位置是 $t_ B^A$ ,点$p$是刚体上的一点。
**一般运动刚体上点的位置:**当坐标系$B$与坐标系$A$不重合,刚体上点p在坐标系A中的坐标该如何描述?
$$
p_A=R_B^A\cdot p_B + t_B^A
$$
$R_B^A$是坐标系$B$相对于坐标系$A$的旋转矩阵,$t_B^A$是坐标系$B$相对于坐标系$A$的平移量,也即坐标系$B$原点在坐标系$A$中的坐标。
引入齐次坐标,将上式变为纯乘法操作:
$$
\widetilde p_A =\begin{bmatrix}p_A \\ 1\\\end{bmatrix},\widetilde p_B =\begin{bmatrix}p_B \\ 1\\\end{bmatrix},T_B^A =\begin{bmatrix}R_B^A& t_B^A \\0^T & 1\\\end{bmatrix}
$$
得到:
$$
\widetilde p_A =T_B^A\cdot \widetilde p_B
$$
其中,$\widetilde p_A$和$\widetilde p_B$为**齐次坐标**,$T_B^A$为齐次坐标$\widetilde p_B$到$\widetilde p_A$的**变换矩阵**
变换矩阵构成**特殊欧氏群**$SE(3)$
$$
SE(3)=\begin{Bmatrix}T=\begin{bmatrix}R & t \\0^T & 1\\\end{bmatrix}\in \mathcal R^{4×4}|R \in SO(3),t \in \mathcal R^{3×1}\\\end{Bmatrix}
$$
变换矩阵的合成法则:两个坐标系之间的变换矩阵可以利用它们与中间坐标系间的变换矩阵相乘得到,该结论可以拓展到多个矩阵
\[T_A^C =T_B^C \cdot T_A^B
\]
变换矩阵的逆
\[T^{-1} =\begin{bmatrix}R^T& -R^Tt \\0^T & 1\\\end{bmatrix}
\]
注意:坐标系\(A\)原点在坐标系\(B\)中的位置
\[t_A^B=-R_A^B\cdot t_B^A=-\begin{pmatrix}R_B^A\end{pmatrix}^T\cdot t_B^A
\]
上式在工程当中有如下常见应用及易错点:
\[t_B^A + t_C^B = t_C^A \\
t_B^A-R_A^C \cdot t_C^A = t_B^A + t_A^C=t_B^C
\]
尤其注意:
\[t_B^A-t_C^A \neq t_B^C
\]




