webgl笔记-1.模型视图矩阵和投影矩阵

最近在学习WebGL技术的过程中，我补充了一些原本了解甚少的计算机图形学知识。如果有同学和我一样，没有系统学过计算机图形学就接触了3D图形编程，而对不少略为艰深的概念有困惑，希望这些笔记能够帮助你。

模型矩阵

我们必须考虑，当空间中点的位置会发生变化的时候，其坐标如何变化。考虑三种基本的变换：平移、旋转和缩放。

“变换”的含义就是，将点的初始位置的坐标P映射到平移、旋转、缩放后的位置坐标P’，即：

$$\begin{bmatrix}x\\y\\z\end{bmatrix}\rightarrow\begin{bmatrix}{x}'\\{y}'\\{z}'\end{bmatrix}$$

平移变换是最简单的变换：

$$\begin{bmatrix}{x}'\\{y}'\\{z}'\end{bmatrix}=\begin{bmatrix}x\\y\\z\end{bmatrix}+\begin{bmatrix}t_{x}\\t_{y}\\t_{z}\end{bmatrix}$$

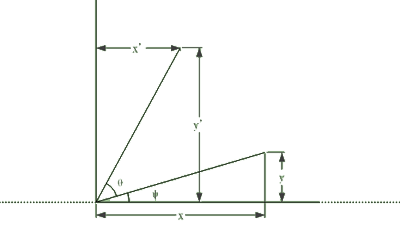
旋转变换有一些复杂，先看在二维平面上的旋转变换：

很容易得到：

$$\begin{matrix}x'=x\cos\theta-y\sin\theta\\y'=x\sin\theta+y\sin\theta\end{matrix}$$

矩阵形式的表达更加简洁，后面大多使用这种形式：

$$\begin{bmatrix}x'\\ y'\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}$$

推广到三维空间中：
点绕z轴旋转：

$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$

点绕x轴旋转：

$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$

点绕y轴旋转：

$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}\cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0\\ \sin\theta & 0 & \cos\theta\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$

绕指定的任意轴旋转变换是由几个绕坐标轴旋转变换和平移变换效果叠加而成的，后文会有详细叙述。

缩放变换也比较简单：

$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}s_{x} & 0 & 0\\ 0 & s_{y} & 0\\ 0 & 0 & s_{z} \end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$

总结一下：平移变换，变换后点坐标等于初始位置点坐标加上一个平移向量；而旋转变换和缩放变换，变换后点坐标等于初始位置点坐标乘以一个变换矩阵。

$$P'=P+T, P'=R\cdot P, P'=S\cdot P$$

齐次坐标这天才的发明，允许平移变换也表示成初始位置点坐标左乘一个变换矩阵的形式。齐次坐标使用4个分量来表示三维空间中的点，前三个分量和普通坐标一样，第四个分量为1。

$$\begin{bmatrix}x\\ y\\ z\end{bmatrix}\rightarrow \begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

平移变换巧妙地表示为：

$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=\begin{bmatrix}1 & 0 & 0 & t_{x}\\ 0 & 1 & 0 & t_{y}\\ 0 & 0 & 1 & t_{z}\\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

旋转变换（以绕z轴旋转为例）和缩放变换相应为：

$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta & 0 & 0\\ \sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=\begin{bmatrix}s_{x} & 0 & 0 & 0\\ 0 & s_{y} & 0 & \\ 0 & 0 & s_{z} & 0\\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

综上，在齐次坐标下三种基本变换实现了形式上的统一，这种形式的统一意义重大。

$$P'=T\cdot P, P'=R\cdot P, P'=S\cdot P$$

矩阵有一个性质：

$$M\cdot (A\cdot B)=(M\cdot A)\cdot B$$

考虑一个点，先进行了一次平移变换，又进行了一次旋转变换，结合上面矩阵的性质，可知变换后的点P’为：

$$P=R\cdot(T\cdot P)=(R\cdot T)\cdot P$$

旋转矩阵和平移矩阵的乘积R·T也是一个4×4的矩阵，这个矩阵代表了一次平移变换和一次旋转变换效果的叠加；如果这个点还要进行变换，只要将新的变换矩阵按照顺序左乘这个矩阵，得到的新矩阵能够表示之前所有变换效果的叠加，将最初的点坐标左乘这个矩阵就能得到一系列变换后最终的点坐标，这个矩阵称为“模型矩阵”。一个模型矩阵乘以另一个模型矩阵得到的还是一个模型矩阵，表示先进行右侧模型矩阵代表的变换，再进行左侧模型矩阵代表的变换这一过程的效果之和，因此模型矩阵的乘法又可以认为是闭合的。
模型矩阵之所以称之为“模型矩阵”，是因为该矩阵与点的位置没有关系，仅仅包含了一系列变换的信息。而在三维世界中，一个模型里所有的顶点往往共享同一个变换，对应同一个模型矩阵，比如抛在空中的一个木块，运转机器的一个齿轮。

之前说到，考虑一个物体绕指定轴旋转，如以下这个变换：绕着过顶点（x，y，z）方向为（a，b，c）的轴旋转角度θ，利用多个变换的叠加构建绕任意轴旋转的变换矩阵。
首先将顶点（x，y，z）平移到原点，绕x轴旋转角度p使指定的旋转轴在x-z平面上，绕y轴旋转角度q使指定的旋转轴与z轴重合，绕指定旋转轴（也就是z轴）旋转角度θ，绕y轴旋转角度-q，绕x轴旋转角度-p,将顶点平移到向量（x，y，z），p和q的值由方向（a，b，c）决定。综上，变换矩阵为：

$$R\begin{pmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix} & \begin{bmatrix}a\\ b\\ c\end{bmatrix} & \theta\end{pmatrix}=T\begin{pmatrix}x\\ y\\ z\end{pmatrix}\cdot R_{x}(-p)\cdot R_{y}(-q)\cdot R_{z}(\theta)\cdot R_{y}(q)\cdot R_{x}(p)\cdot T\begin{pmatrix}-x\\ -y\\ -z\end{pmatrix}$$

因此在处理围绕非坐标轴旋转的模型时，根据指定的旋转参数可以直接按照上述公式生成按照指定轴旋转的旋转矩阵，参加模型矩阵的构建。

齐次坐标还有一个优点，能够区分点和向量：在普通坐标里，点和向量都是由三个分量组成的，表示位置的点坐标（2，3，4）和表示方向的向量（2，3，4）没有区别。而在齐次坐标中，第四个分量可以区分它们，点坐标的第四个分量为1，而向量坐标第四个分量为0。比如，平移一个点是有意义的，能够得到平移后的点坐标；而平移一个向量是没有意义的，方向不会因为平移而改变。

以上，我们已经了解到模型矩阵可以存储一个模型空间位置变化的信息，在生成三维动画每一帧的过程中，我们首先计算每个模型的模型矩阵，然后将最初的模型的每一顶点坐标都左乘该模型矩阵，得到这一帧表示的时刻（模型已经经过多次变换）该模型每一顶点的坐标。上面说的“帧”并不狭义地指屏幕的两次刷新时间的短暂间隔中屏幕上呈现的图像，而是指在这幅图像所描绘的整个三维空间的这个瞬间的所有顶点的位置。

来看个具体的例子：一个绕z轴匀速螺旋匀速上升的立方体，在某一帧中（即在这一帧对应的时刻t下），其向z轴正方向平移的长度和绕z轴旋转的角度分别为：

$$t_{z}=t\cdot v_{t},\theta_{z}=t\cdot \omega_{t}$$

则模型矩阵（注意上文齐次坐标下的基本变换矩阵）为：

$$mMatrix=R_{z}(\theta_{z})\cdot T(0,0,t_{z})=\begin{bmatrix}\cos\theta_{z} & -\sin\theta_{z} & 0 & 0\\ \sin\theta_{z} & \cos\theta_{z} & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & t_{z}\\ 0 & 0 & 0 & 1\end{bmatrix}$$

产生这一帧时，只需要计算一次模型矩阵，再将立方体中8个顶点坐标分别左乘该矩阵，就可以得到经过变换后8个顶点的坐标。当一个模型顶点数量增加到上百甚至上千个，模型变换的步骤数也增加到几十步时，模型矩阵的作用就很明显了：如果没有齐次坐标（也当然没有模型矩阵），对每个顶点都需要一步一步地变换：平移的时候加上一个向量，旋转的时候左乘一个矩阵，才能得到变换后的顶点坐标；而模型变换只需要计算一次模型矩阵（当然也是一步一步的），然后每个顶点左乘模型矩阵就可以直接得到变换后的坐标了。

视图矩阵

在模型矩阵中，我们关心的是空间中的点在经历变换后在世界坐标系下的位置。事实上，我们更加关心空间中的点相对于观察者的位置。最简单的方案是将观察者置于原点处，面向z轴（或x轴、y轴）正半轴，那么空间中的点在世界坐标系下的位置就是其相对于观察者的位置。
观察者的位置和方向会变化，看上去就好像整个世界的位置和方向发生变化了一样，所以解决的方案很简单，将世界里的所有模型看作一个大模型，在所有模型矩阵的左侧再乘以一个表示整个世界变换的模型矩阵，就可以了。这个表示整个世界变换的矩阵又称为“视图矩阵”，因为他们经常一起工作，所以将视图矩阵乘以模型矩阵得到的矩阵称为“模型视图矩阵”。模型视图矩阵的作用是：乘以一个点坐标，获得一个新的点坐标，获得的点坐标表示点在世界里变换，观察者也变换后，点相对于观察者的位置。

视图矩阵同样也可以分为平移、旋转和缩放，视图矩阵是将观察者视为一个模型，获得的观察者在世界中变换的模型矩阵的逆矩阵。

观察者平移了（tx，ty，tz），视图矩阵如下，可以看出如果将视图矩阵看作整个世界的模型矩阵，相当于整个世界平移了（-tx，-ty，-tz）。

$$\begin{bmatrix}1 & 0 & 0 & t_{x}\\ 0 & 1 & 0 & t_{y}\\ 0 & 0 & 1 & t_{z}\\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1}=\begin{bmatrix}1 & 0 & 0 & -t_{x}\\ 0 & 1 & 0 & -t_{y}\\ 0 & 0 & 1 & -t_{z}\\ 0 & 0 & 0 & 1 \end{bmatrix}$$

观察者绕z轴旋转了角度θ，视图矩阵如下，相当于整个世界绕z轴旋转了-θ度。

$$\begin{bmatrix}\cos\theta & -\sin\theta & 0 & 0\\ \sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1}=\begin{bmatrix}\cos\theta & \sin\theta & 0 & 0\\ -\sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{bmatrix}$$

观察者在三个方向等比例缩小了s倍，视图矩阵如下，相当于整个世界放大了s倍。

$$\begin{bmatrix}s_{x} & 0 & 0 & 0\\ 0 & s_{y} & 0 & 0\\ 0 & 0 & s_{z} & 0\\ 0 & 0 & 0 & 1\end{bmatrix}^{-1}=\begin{bmatrix}1/s_{x} & 0 & 0 & 0\\ 0 & 1/s_{y} & 0 & 0\\ 0 & 0 & 1/s_{z} & 0\\ 0 & 0 & 0 & 1\end{bmatrix}$$

观察者缩小的情形可能会引起困惑：如果人和猫咪的眼睛在同一个位置，人看到的世界和一只猫咪看到的世界应当是一样尺寸的，这和上述视图矩阵的情形矛盾；但是直觉告诉我，如果你喝了缩小药水，你应该会觉得整个世界在膨胀，就像视图矩阵所表现的那样。解答是这样：如果在计算机上模拟观察者喝了缩小药水的情形，在屏幕上看到整个世界是膨胀的，因为在那个虚拟的三维空间中，计算机屏幕这个“窗口”也随你（观察者）缩小。
视图矩阵实际上就是整个世界的模型矩阵，这给我一点启发：一个模型可能由多个较小的子模型组成，模型自身有其模型矩阵，而子模型也有自己的局部模型矩阵。考虑一辆行驶中的汽车的轮胎，其模型视图矩阵是局部模型矩阵（描述轮胎的旋转）左乘汽车的模型矩阵（描述汽车的行驶）再左乘视图矩阵得到的。

投影矩阵

模型视图矩阵的作用是确定某一帧中，空间里每个顶点的坐标，而投影矩阵则将这些顶点坐标映射到二维的屏幕上，即：

$$\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}\rightarrow \begin{bmatrix}x'\\ y'\end{bmatrix}$$

最主要的有两种投影方式，正射投影和透视投影。前者用于精确制图，如工业零件侧视图或建筑物顶视图，从屏幕上就可以量测平行于屏幕的线段长度；后者用于模拟视觉，远处的物体看上去较小。下图中，空间中的同一个矩形，正射投影后仍然是矩形，而透视投影后则变成了梯形。

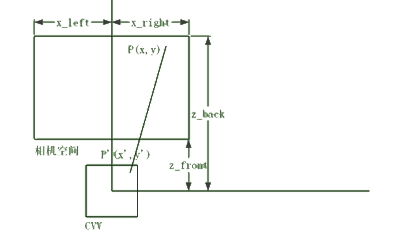
正射投影（投影面和相机空间）：

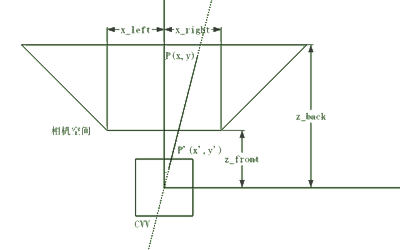
透视投影（投影面和相机空间）：

三维世界的显示中，屏幕模拟了一个窗口，你透过这个窗口观察“外面”的世界。你的屏幕是有边缘的（除非你有一个球形的房间，内壁全是屏幕），因此你仅仅能观察到那个世界的一部分，即“相机空间”。相机空间的左、右、上、下边界是受限于屏幕的边缘，同时也设定前、后边界，因为你很难看清太近或太远的东西。在正射投影中，相机空间是一个规则的立方体，而在透视投影中则是一个方台体。
三维模型可能在不同的显示器上展现，因此投影的过程中不该将显示器参数加入进来，而是将空间中的点投影到一个规范的显示器中。另外，透视投影中的z值并不是毫无用处，它可以用来表示顶点的“深度”：如果三维空间中的两个不同顶点投影到平面上时重合了，那么将显示深度较浅的顶点。

定义一个规范的视窗区域（CCV），为x，y，z都处在区间[-1,1]之间的边长为2的立方体。x和y坐标值用来线形拉伸到到实际屏幕上，而z值存储了“深度”。而投影的过程就是将三维空间中的点从相机空间映射到CCV中。
正射投影非常简单，直接将矩形的相机空间线形压缩到CCV中即可。采取顶视图，相机空间的左右边界为 $x_{left}$ 和 $x_{right}$ :

简单的线形成比例关系：

$$\frac{x-x_{left}}{x_{right}-x_{left}}=\frac{x'-(-1)}{1-(-1)}$$

$$x'=\frac{2}{x_{right}-x_{left}}\cdot x-\frac{x_{right}+x_{left}}{x_{right}-x_{left}}$$

推广到y轴和z轴：

$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=\begin{bmatrix}\frac{2}{x_{right}-x{left}} & 0 & 0 & -\frac{x_{right}+x_{left}}{x_{right}-x_{left}}\\ 0 & \frac{2}{y_{top}-y_{bottom}} & 0 & -\frac{y_{top}+y_{bottom}}{y_{top}-y_{bottom}}\\ 0 & 0 & \frac{2}{z_{back}-z_{front}} & -\frac{z_{back}+z_{front}}{z_{back}-z_{front}}\\ 0 & 0 & 0 & 1\end{bmatrix}\cdot \begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

相机空间中的点经过正射投影矩阵左乘后得到的点都在CCV之中：

$$\begin{matrix}-1<x'<1\\ -1<y'<1\\ -1<z'<1\end{matrix}$$

透视投影相对较为复杂，同样用顶视图考虑x坐标的情况：

$$\frac{x_{p}}{h}=\frac{x}{z}$$

$$\frac{x_{p}-x_{left}}{x_{right}-x_{left}}=\frac{x'-(-1)}{1-(-1)}$$

$$x'=\frac{1}{z}\cdot \frac{2h}{x_{right}-x_{left}}-\frac{x_{right}+x_{left}}{x_{right}-x_{left}}$$

转化为齐次的方式：

$$z\cdot x'=x\cdot \frac{2h}{x_{right}-x_{left}}-\frac{x_{right}+x_{left}}{x_{right}-x_{left}}$$

推广到y轴：

$$\begin{bmatrix}z\cdot x'\\ z\cdot y'\\ z\cdot z'\\ z\end{bmatrix}=\begin{bmatrix}\frac{2}{x_{right}-x{left}} & 0 & -\frac{x_{right}+x_{left}}{x_{right}-x_{left}} & 0\\ 0 & \frac{2}{y_{top}-y_{bottom}} & -\frac{y_{top}+y_{bottom}}{y_{top}-y_{bottom}} & 0\\ 0 & 0 & t_{z} & s_{z}\\ 0 & 0 & 1 & 0\end{bmatrix}\cdot \begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

透视投影矩阵的第三行不是我们关心的内容，只要保证不同顶点投影前后的点坐标的第三个分量z和z’的大小关系不变就可以。
透视投影矩阵尾行是（0，0，1，0），这样就将计算得到的坐标的第四个分量赋值为z而不是1。将相机空间左乘投影矩阵后的结果不是一个CCV空间，如果你将这个空间画出来，会发现其仍然是一个方台形。这时进行“透视除法”，将上一步得到的点坐标化为第四个分量为1的标准齐次坐标：

$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=\begin{bmatrix}z\cdot x'\\ z\cdot y'\\ z\cdot z'\\ z'\end{bmatrix}\cdot \frac{1}{z}$$

然后我们直接取齐次坐标中的x’和y’值，并将其线形映射到屏幕上，比如点（0，0）出现在屏幕中央，点（-1，1）出现在屏幕左上角。

WebGL

WebGL中对于模型视图矩阵和投影矩阵的操作依赖于第三方库，比如Oak3D或glMatrix，WebGL本身不支持（或者说不限制）任何对模型视图矩阵和投影矩阵的操作。
WebGL是在浏览器端运行的，所以使用JavaScript编程。下面的代码来自www.hiwebgl.com翻译的LearningWebGL.com的WebGL教程。以glMatrix库为例：

// 新建空模型视图矩阵 
var mvMatrix = mat4.create(); 
// 将矩阵设置为单位阵 
mat4.identity(mvMatrix); 
// 平移和旋转 
mat4.translate(mvMatrix, [-1.5, 0.0, -8.0]); 
mat4.rotate(mvMatrix, degToRad(45), [0, 1, 0]);

将矩阵设置为单位阵相当于说：“这个矩阵表示什么都还没做（平移、旋转、缩放）呢”，事实上，任意点坐标乘以单位矩阵都只能得到自己，正说明“什么都没做”。 

平移矩阵的函数mat4.translate()做的仅仅是将mvMatrix左乘一个平移矩阵而已。

旋转矩阵的函数mat4.rotate()也许比较复杂，它做的是上面我们讨论过的“围绕任意轴旋转”的问题，这个函数默认使用“本地轴”，即过所有平移效果累加后的那一点的轴，参数向量[0,1,0]是轴的指向，因此上面的函数调用处理了一个围绕本地y轴的旋转。

// 新建空投影矩阵 
var pMatrix = mat4.create(); 
// 初始化投影矩阵 
mat4.perspective(45, gl.viewportWidth / gl.viewportHeight, 0.1, 100.0, pMatrix);

投影矩阵不会因为场景里模型的位置变化或观察者的移动而变化（当然如果你想模拟观察者戴眼镜的过程你可能要考虑），故而投影矩阵只需要一次初始化就够了。初始化需要给出相机空间的前、后、左、右、上、下边界，很容易从函数调用里传入的参数推知：包括前、后边界，相机空间的宽高比和水平视场角。 

如果你使用脚本调试工具监测矩阵对象mvMatrix和pMatrix，就会发现他们仅仅是有16个元素的Float32Array对象而已，你完全可以亲自处理它。

值得一提的是glMatrix库的函数大多不返回处理后的矩阵，在将矩阵作为参数传入时已经给了函数修改矩阵的权利，很少的情况下需要会写这样的代码（但其他的库不一定这样）：

xMatrix = matX.operate();

使用库函数或自力更生处理完矩阵后，通过着色器程序传递到着色器中（着色器程序是JavaScript脚本里的概念，而着色器是用其他脚本语言编写的在显卡中运行的逻辑，这些不在本文的讨论范围内）：

// 设置着色器程序 
…… 
shaderProgram.pMatrixUniform = gl.getUniformLocation(shaderProgram, "uPMatrix"); 
shaderProgram.mvMatrixUniform = gl.getUniformLocation(shaderProgram, "uMVMatrix"); 
…… 
// 将模型视图矩阵和投影矩阵传入着色器 
gl.uniformMatrix4fv(shaderProgram.pMatrixUniform, false, pMatrix); 
gl.uniformMatrix4fv(shaderProgram.mvMatrixUniform, false, mvMatrix);

然后看看着色器里的代码，这是用x-shader类型的脚本语言写的：

void main(void){ 
        …… 
        gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0); 
        …… 
}

 可以看到屏幕上点坐标由初始点坐标左乘模型视图矩阵，再左乘投影矩阵得到的。对于较复杂的场景，我猜测可能需要重新编写着色器，将模型矩阵和视图矩阵拆开处理。

综上所述，模型视图矩阵和投影矩阵是三维计算机图形学的基石。关于这两个矩阵的知识虽然不是进行3D图形编程的必须，但是至少能够帮助我们更好地了解那些库函数在做些什么，或者自己直接操作矩阵对象。

其他

我写这篇博文参考了：
1. Donald Hearn & M. Pauline Baker 的著作《计算机图形学》
2. 这一篇关于投影矩阵的博文：http://blog.csdn.net/yanwei2016/article/details/7326180（虽然题目是模型视图矩阵变化，但大部分篇幅都在讲投影矩阵）
3. 站点www.hiwebgl.com翻译的LearningWebGL.com的WebGL教程