221.Maximal Square

问题描述：

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

Example:

Input: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Output: 4

解题思路：

　　这道题可以用动态规划来解，为O(n²)的时间复杂度

　　建立一个二维的dp数组，里面dp[i][j]存的是可形成的以（i,j）为右下角的正方形的最长的边长。

　　那么dp[i][j] = min(dp[i-1][j-1], min(dp[i][j-1], dp[i-1][j]) + 1

如下图所示：

　　

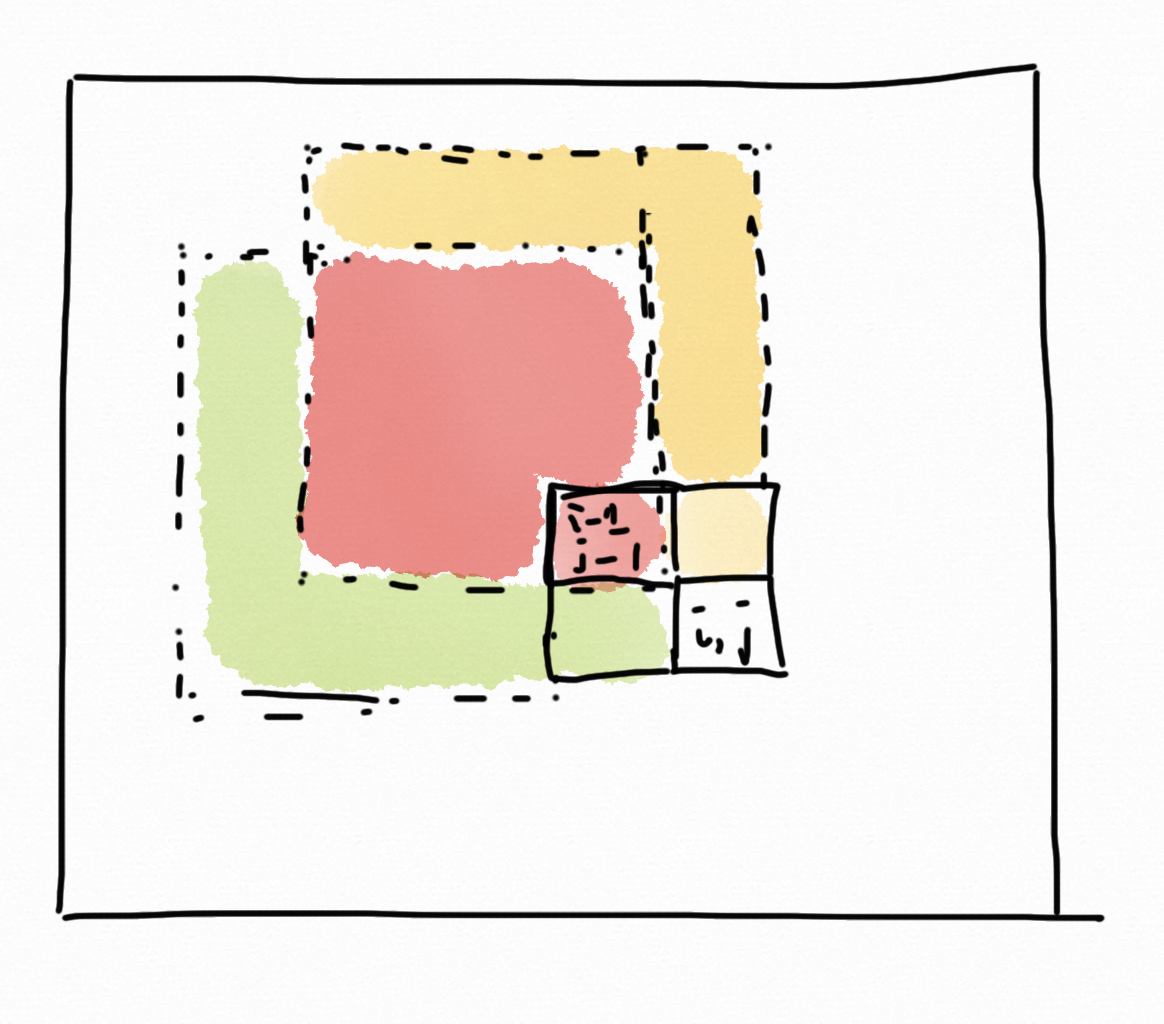
(i-1, j-1)能够形成的最大正方形为红色区域

(i-1, j)能够形成的最大正方形为红色区域+黄色区域

(i, j-1)能够形成的最大正方形为红色区域+绿色区域

若左上角不为0的话那么红色区域也会扩展至包含左上角

若(i-1, j)比红色区域要小2及其以上的话，红色区域也会缩小，因为他们很有大一部分是重叠的。

 

注意！因为要返回的是面积所以需要平方。

 

代码：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty() || matrix[0].empty())
            return 0;
        int m = matrix.size();
        int n = matrix[0].size();
        int ret = 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(i == 0 || j == 0){
                    dp[i][j] = (matrix[i][j] == '1') ? 1 : 0;
                }else{
                    if(matrix[i][j] == '1'){
                        dp[i][j] = min(dp[i - 1][j - 1], min(dp[i-1][j], dp[i][j-1])) + 1;
                    }
                }
                ret = max(ret, dp[i][j]);
            }
        }
        return ret*ret;
    }
};

 类似题目：

62. Unique Paths

63. Unique Paths II

72. Edit Distance