1. 二项堆数据结构简介
2. 存储模型
3. 实现代码分析
4. 参考资料及代码下载
<1>. 二项堆数据结构简介
一颗二项堆是由一组二项树组成,在给出二项堆的定义之前,首先我们来定义什么是二项树。
二项树是一种递归的定义:
1. 二项树B[0]仅仅包含一个节点
2. B[k]是由两棵B[k-1]二项树组成,其中一颗树是另外一颗树的子树。
下面是B0 - B4二项树:

显然二项树具有如下的性质:
1. 对于树B[k]该树含有2^k个节点;
2. 树的高度是k;
3. 在深度为i中含有Cik节点,其中i = 0, 1,2 ... , k;
定义完二项树之后,下面来定义二项堆H,二项堆是由一组满足下面的二项树组成:
1. H中的每个二项树遵循最小堆性质;
2. 对于任意的整数k的话,在H不存在另外一个度数也是k的二项树;
另外定义:
1. 二项堆的度数定义成子女个数;
2. 定义二项堆的根表是二项树的根节点形成的链表;
好的,二项堆的定义完成之后,下面的问题就是我们在什么情况下使用“二项堆”?
如果是不支持所谓的合并操作union的话,普通的堆的数据结构就是一种很理想的数据结构。 但是如果想要支持集合上的合并操作的话,最好是使用二项堆或者是斐波那契堆,普通的堆在union操作上最差的情况是O(n),但是二项堆和斐波那契堆是O(lgn)。
<2>. 存储模型
了解了什么二项堆的定义和使用场景之后,我们来看看如何存储二项堆?
首先定义二项堆中每个节点的类型:
1. parent:指向父节点
2. sibling:指向右边的兄弟节点
3. child:定义该节点的子节点
4. degree:定义该节点的度数
5. 其他应用场景中需要的数据
struct heap_node {
struct heap_node* parent;
struct heap_node* next;
struct heap_node* child;
unsigned int degree;
void* value;
struct heap_node** ref;
};
对于定义的字段,对于根表中的节点和非根表中的元素是不相同的,根表中的节点的parent全部是空,sibling指向的是根表中的下一个元素;对于非根表中的节点的话,parent指向的是该节点的父节点,sibling指向该节点的兄弟节点。
定义二项堆数据类型:
1. 根表的头节点
2. 其他应用需要的数据
struct heap {
struct heap_node* head;
struct heap_node* min;
};
<3>. 算法分析
3.1 初始化二项堆
仅仅将根表的头节点指向null:
static inline void heap_init(struct heap* heap)
{
heap->head = NULL;
heap->min = NULL; // 其他操作
}
3.2 寻找最小关键字
由于二项堆中每个二项树都是遵循最小堆性质的,所以最小元素一定是在根表中,遍历根表一次即可找出最小元素:
// 通过node返回二项堆中的最小元素,同时
// 通过prev指针返回最小元素node的前一个节点
// 指针
static inline void __heap_min(heap_prio_t higher_prio, struct heap* heap,
struct heap_node** prev, struct heap_node** node)
{
struct heap_node *_prev, *cur;
*prev = NULL;
// 如果二项堆为空
if (!heap->head) {
*node = NULL;
return;
}
*node = heap->head; // 保存最小元素节点指针,初始默认head是最小
_prev = heap->head; // 前一个节点指针
cur = heap->head->next;
while (cur) {
if (higher_prio(cur, *node)) {
// 找到更小的节点
*node = cur;
*prev = _prev;
}
_prev = cur;
cur = cur->next;
}
}
3.3 合并操作
二项堆的合并操作是一个比较复杂的过程,这里假设需要合并的两个二项堆是H1和H2,如果简单的将H1和H2的根表(两个链表)进行合并的话,显然这可能是违反了二项堆定义的第二条:
2. B[k]是由两棵B[k-1]二项树组成,其中一颗树是另外一颗树的子树。
这就是二项堆合并操作的主要需要解决的问题:两个二项堆合并完成之后,可能在根表中存在两个度数相同的节点,需要将度数相同的节点合并成一个新的节点。
这里我们进一步将这个问题现在转换成了:已知H1根表和H2的根表中每个节点的度数,并且H1和H2的根表已经是按照度数排序的,如何H1和H2根表合并,并且新的根表中不存在两个度数相同的节点。
一个朴素的思想就是现将H1和H2合并,然后在进行适当的调整,将两个度数相同的节点合并掉,这样保证了新的根表中不存你在两个度数相同的节点。那么基本的程序框架:
union(H1, H2)
{
#1:合并H1和H2的根表,生成新的根表H,并且H的节点是按照度数排序的;
#2:将H中度数相同的两个节点合并,直到根表H中不存在两个度数相同的节点;
}
继续细化上面的思路,#1是比较简单的,类似于归并排序中的合并的思路,但是对于#2而言,由于H是排序完成的,那么我们仅仅需要将H遍历一遍,如果存在两个相同的度数,合并即可。
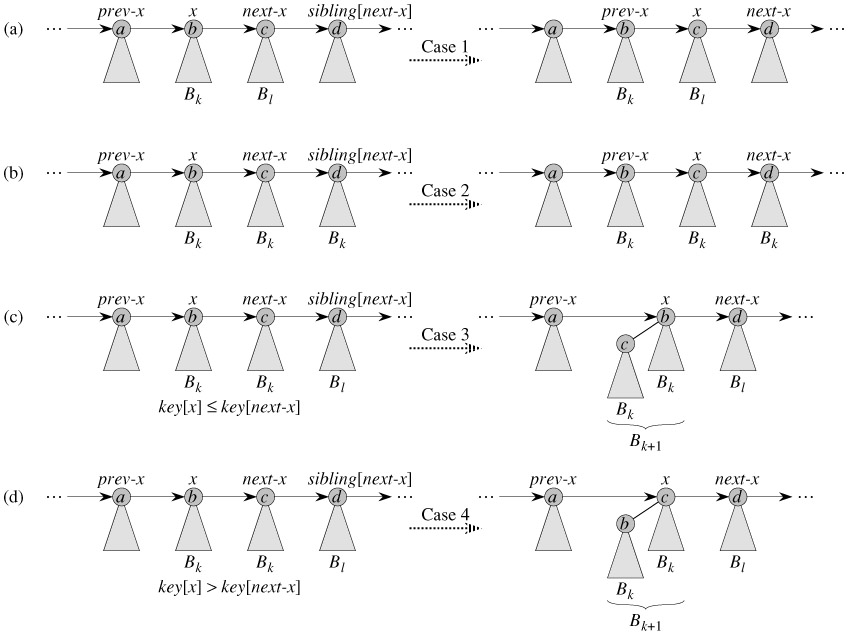

// 合并两个二项堆
static inline void __heap_union(heap_prio_t higher_prio, struct heap* heap,
struct heap_node* h2)
{
struct heap_node* h1;
struct heap_node *prev, *x, *next;
if (!h2)
return;
h1 = heap->head;
if (!h1) {
heap->head = h2;
return;
}
// 合并两个根表
h1 = __heap_merge(h1, h2);
prev = NULL;
x = h1;
next = x->next;
// 将新合并的根表中度数相同的节点合并
while (next) {
// case 1和case 2
if (x->degree != next->degree ||
(next->next && next->next->degree == x->degree)) {
/* nothing to do, advance */
prev = x;
x = next;
} else if (higher_prio(x, next)) {
// case 3
/* x becomes the root of next */
x->next = next->next;
__heap_link(x, next);
} else {
// case 4
/* next becomes the root of x */
if (prev)
prev->next = next;
else
h1 = next;
__heap_link(next, x);
x = next;
}
next = x->next;
}
heap->head = h1;
}
其中__heap_link是一个辅助函数,函数如下:
/* make child a subtree of root,使child参数指向的节点成为root节点的孩子节点 */
static inline void __heap_link(struct heap_node* root,
struct heap_node* child)
{
child->parent = root;
child->next = root->child;
root->child = child;
root->degree++;
}
3.4 抽取最小关键字节点
BINOMIAL-HEAP-EXTRACT-MIN(H)
find the root x with the minimum key in the root list of H,
and remove x from the root list of H
H' MAKE-BINOMIAL-HEAP()
reverse the order of the linked list of x's children,
and set head[H'] to point to the head of the resulting list
H BINOMIAL-HEAP-UNION(H,H')
return x
// 抽取最小关键字
static inline struct heap_node* __heap_extract_min(heap_prio_t higher_prio,
struct heap* heap)
{
struct heap_node *prev, *node;
// 找到最小节点,存储在node中,prev变量中存储的是
// node节点的前一个节点
__heap_min(higher_prio, heap, &prev, &node);
if (!node) // 根表为空的话
return NULL;
/*
如果prev不空,也就是说明最小元素不是根表的
第一元素
*/
if (prev)
prev->next = node->next; // 将node节点从根表中摘除
/*
如果node(最小元素的值)节点是根表的第一个元素的话,直接将
修改二项堆的head指针
*/
else
heap->head = node->next;
/*
调用__heap_reverse将node节点的子节点反转输出,
和堆heap合并
*/
__heap_union(higher_prio, heap, __heap_reverse(node->child));
// 返回该最小节点
return node;
}
3.4 减小关键字的值
这个算法和堆中的算法是相类似的,如果将某个节点的值减少之后,可能违反最小堆的性质,那么将沿着父节点开始向上移动,修改节点的值。
BINOMIAL-HEAP-DECREASE-KEY (H,x,k)
if k > key[x]
then error "new key is greater than current key"
key[x] = k
y = x
z = p[y]
while z != NIL and key[y] < key[z]
do exchange key[y] key[z]
// If y and z have satellite fields, exchange them, too.
y = z
z = p[y]
// 减少关键字的值
static inline void heap_decrease(heap_prio_t higher_prio, struct heap* heap,
struct heap_node* node)
{
struct heap_node *parent;
struct heap_node** tmp_ref;
void* tmp;
/* node's priority was decreased, we need to update its position */
if (!node->ref)
return;
if (heap->min != node) {
/* bubble up开始和父节点交换数据,直到符合最小堆的性质 */
parent = node->parent;
while (parent && higher_prio(node, parent)) {
/* swap parent and node */
tmp = parent->value;
parent->value = node->value;
node->value = tmp;
/* swap references */
if (parent->ref)
*(parent->ref) = node;
*(node->ref) = parent;
tmp_ref = parent->ref;
parent->ref = node->ref;
node->ref = tmp_ref;
/* step up */
node = parent;
parent = node->parent;
}
}
}
3.5 删除一个节点
这里使用的算法是比较简单的,首先减小需要删除的节点的关键字的值,然后通过调用函数BINOMIAL-HEAP-EXTRACT-MIN将该节点从二项堆中删除。算法的伪代码如下:
BINOMIAL-HEAP-DELETE(H,x)
BINOMIAL-HEAP-DECREASE-KEY(H,x,-)
BINOMIAL-HEAP-EXTRACT-MIN(H)
<4>. 参考资料及代码下载
算法导论:http://net.pku.edu.cn/~course/cs101/2007/resource/Intro2Algorithm/book6/chap20.htm
代码下载:/Files/xuqiang/algorithm/BinomialHeapUsingC.rar








 浙公网安备 33010602011771号
浙公网安备 33010602011771号