Chapter 7:Statistical-Model-Based Methods
作者:桂。
时间:2017-05-25 10:14:21
主要是《Speech enhancement: theory and practice》的读书笔记,全部内容可以点击这里。
书中代码:http://pan.baidu.com/s/1hsj4Wlu,提取密码:9dmi
前言
最近学习有一点体会,每一个学科的理论模型都提供了解决问题的思路,一个没有受过教育又迷信权威的头脑,难以从抽象的角度去认识、理解问题,自然科学传递了这样一套思维。例如之前的谱减法,就是具体问题具体分析;维纳滤波,表达了复盘、以及反馈总结的重要性;这一章的统计模型,表达了对于不善于长期记忆的人类,借助历史信息可以获得更多的益处。总结一下,这些模型都表明:认识问题要经过感性-理性-感性的往复过程,很难有一劳永逸的方法,这也提醒思考的时候要小心、并保持客观(因为总有新问题),避免陷入刚愎自用的误区,同时也不必灰心丧气,从Ada-boost的角度来看,任何弱分类器都可以组合成强分类器,自己/他人的经历、经验增加(无论真假,只要努力推理出真与假的倾向),一个基本事实是:合理利用这些信息,总会让人更接近事实真相。具体来说,对于语音降噪,都有:意识到问题——拆解并解决问题 的步骤,这也说明了一个现象:学习、记忆、认知,这些 靠眼耳鼻舌身意 直观接受的过程,如果二次加工,那么效果将会进一步提升。
这一章主要是利用统计模型,细节处打算跳过,主要是三种模型:最大似然估计ML、最小均方误差估计MMSE、最大后验估计MAP。
一、最大似然估计:MAXIMUM-LIKELIHOOD ESTIMATORS
A-最大似然估计
加性噪声模型

写成幅频形式
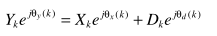
为了求解,给出两点假设:1) 虽然未知,但是确定信号,而不是随机信号;2)噪声是复高斯分布,且实部、虚部的方差相同;
虽然未知,但是确定信号,而不是随机信号;2)噪声是复高斯分布,且实部、虚部的方差相同;
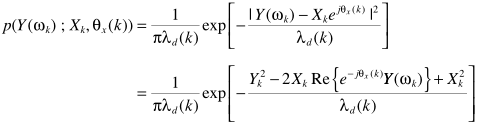
这个求解比较复杂,且仍然可以用带噪声的相位近似 ,这样一来
,这样一来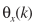 就是无关紧要的了,可以对上面的式子进一步处理:
就是无关紧要的了,可以对上面的式子进一步处理:

这里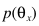 是未知的,这里强行用了另一个约束:在没有先验的情况下,均匀分布信息量最大,也就是不确定性最大,这也符合没有先验之一预期,从而
是未知的,这里强行用了另一个约束:在没有先验的情况下,均匀分布信息量最大,也就是不确定性最大,这也符合没有先验之一预期,从而

上式简化为
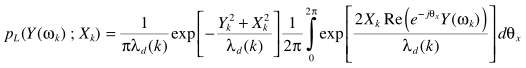
这里积分部分满足Bessel的定义

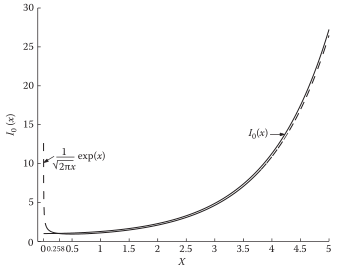
零阶Bessel可近似:
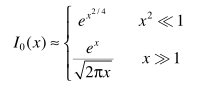
近似的结果
利用Bessel近似表达似然函数
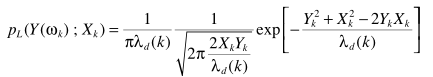
导数为零求解出幅度谱估计
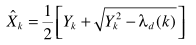
恢复降噪的信号
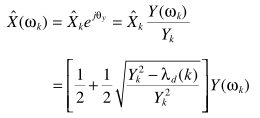
从这一结果也可以看出X = 1/2Y + 1/2HY,总是有部分保留,ML衰减是较小的,也正因为如此,ML估计器基本不单独使用,需要配合其他模型使用:如利用语音不存在概率。
B-功率谱减
与ML估计器不同,这里不再假定 是确定信号,而是随机信号。
是确定信号,而是随机信号。
既然是随机信号,就有统计信息。因此给出假设:噪声、语音信号的DFT不相关,且都服从零均值的高斯分布。从而得出Y概率密度

容易估计幅度谱

得到恢复的音频
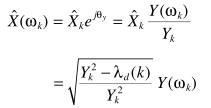
这就是功率谱减,即(γ为后验信噪比)

C-维纳滤波
对于维纳滤波器

变换一下形式
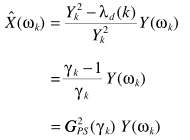
滤波器是功率谱减的级联,因此衰减最大。
总计一下:按衰减程度由大到小,关系依次是:维纳滤波>功率谱减>最大似然估计

二、贝叶斯估计 BAYESIAN ESTIMATORS
A-MMSE幅值估计器
基于短时频谱幅值的方法有个专业术语: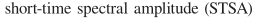 ,最优幅度谱估计:
,最优幅度谱估计:
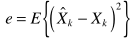
根据联合密度
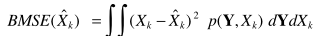
得到最优估计器

看着感觉跟Wiener滤波器一回事,其实是有区别的:1)Wiener中,X = HY,假设有线性关系,这里没有线性这一约束,也就是说这里的估计器可以是非线性的; 2)维纳的MMSE是复频谱最优 ,而此处的MMSE是幅度谱最优。
,而此处的MMSE是幅度谱最优。
同样是为了简化,引入约束1:各个频点的DFT系数相互独立:
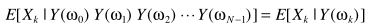
这样一来求解问题简化为:
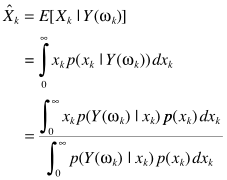
由于复信号Y是关于Xk和theta的函数,难以直接求取 ,只要利用联合分布积分处理即可
,只要利用联合分布积分处理即可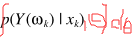 ,也就是
,也就是

这样一来求解红框里的两个方程就可以得出理论解。这里引入约束2:Y是两个零均值的复高斯随机变量之和。
则

这里用到复高斯概率密度的性质:
如果:
且
则
且两高斯分布:其模值为瑞利分布,相位为均匀分布,且二者独立,证明可以参考这里。从而
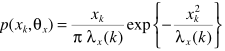
事实上,至此完成了问题的求解,得到Xk的估计。但牛人们非要给一个更简洁的表达式,这里直接给出结果:

具体参数的定义,直接引用原文:

理论模型搭建完成,甚至得出了更简洁的形式,距离应用只差一步——参数的近似估计。文中的基本方法有两个:
1-Maximum-Likelihood Method
利用多帧信号: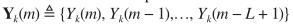 ,求解似然方程
,求解似然方程

容易得出估计(因为是非零,所以max(估值,0)修正一下)

从而有
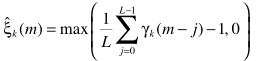
2-Decision-Directed Approach
根据定义

进一步写成

一个常规的思路是分两边看,借助递归思想,因为:
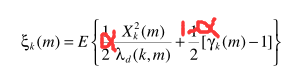
得出递归的更新公式

至此,完成了MMSE从理论到应用的整个过程。
B-MMSE复数估计器
上面是幅值估计,相位用的是带噪信号的相位,可不可以直接对复信号利用MMSE进行估计呢?
求解问题转化为:分别利用MMSE求解幅值、相位的最优解,幅值已解决,直接分析相位

可以得出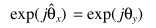 ,所以带噪信号的相位是干净信号相位在MMSE下的最优解。
,所以带噪信号的相位是干净信号相位在MMSE下的最优解。
C-对数MMSE估计器
求解思路与幅值的MMSE完全相同,不同的是利用对数的差异性

首先带来一个问题:为什么要用Log-MMSE?个人理解是logx - logy = logx/y,min|x/y|等价于min(x-y)2 s.t. y2 = c,c为常数。log相比于直接MMSE,保证干净信号幅值不变(不失真)的前提下,误差最小化,有点类似维纳滤波与LCMV之间的关系。理论上直接求解估值

无法直接求解,利用矩量简化求解
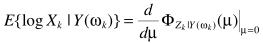
其中

跟MMSE求解一个思路,至此完成求解。但牛人们也希望简化

从而实现简化求解
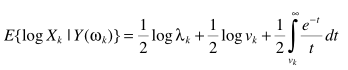
vk, λk跟上面的定义一样,进一步简化
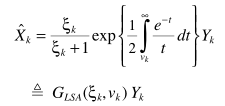
参数估计与MMSE中的思路完全一致,至此完成了求解以及实际应用的实现,其中积分部分也可以利用级数展开来简化

Log-MMSE比MMSE抑制性更好:

D-pTH-POWER SPECTRUM-P阶求解
先说结论:p阶是更广义的形式,Linear MMSE是它的特例,Log-MMSE也可以用p阶来实现逼近
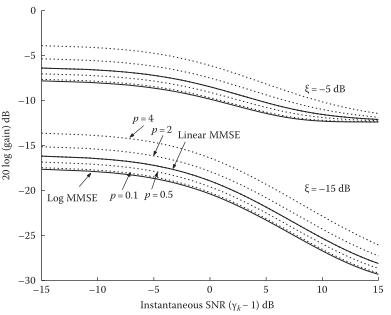
下面理论分析一下,给出准则函数

得出最优估计

都是一样的套路:不能直接求解,转化问题
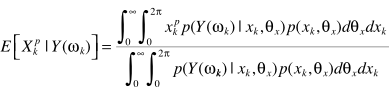
大牛们求解的结果
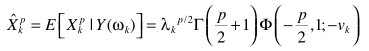
即

具体参数求解同MMSE中的方法。
E-非高斯分布MMSE估计器
上面的DFT系数分布,都假设为高斯分布,实际情况是分布可能更接近其他分布(按频点统计):如拉普拉斯、伽马分布等等,这就需要考虑其他概率模型
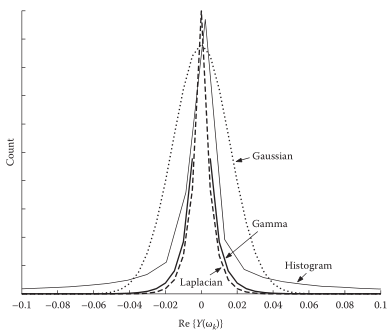
一个合理的约束:DFT系数实部、虚部统计独立。这样互不相干,可以分别得出MMSE估计器,再进行拼接:
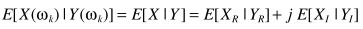
其他思路都是一样的,就是最后解方程一般人解不动...说一下思路:
根据贝叶斯定理

同样只要估计出P(Y|X)和P(Y)就完成求解

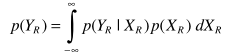
从而得出估计器,完成求解

大牛总是可以简化问题的,虽然这次的简化好像也不漂亮:
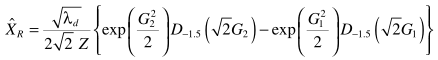
其中

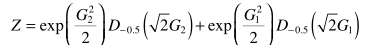
以上是基于Gamma分布的推导,这里只是提供了一个笼统的思维框架。放在具体问题,需要:统计实验数据,并估计概率模型→基于合理的概率模型,得到用来增强的估计器。
三、最大后验估计 MAXIMUM a POStErIOrI (MAP) ESTIMATORS
A-幅值、相位估计器
准则函数
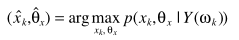
利用贝叶斯准则
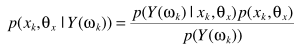
分母不影响参数的估计,忽略
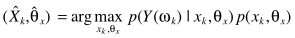
约束来了:1)DFT系数实部、虚部都是高斯分布;2)二者统计独立,从而有
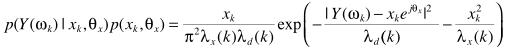
这样一来,求解就容易了

偏导为零,得出估计器
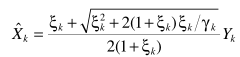

实际应用中具体参数的估计,与上面的思路都是一致的。
B-幅值估计器
只估计幅值:
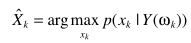
贝叶斯准则

忽略分母

利用

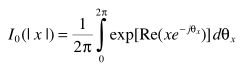
并借助A中的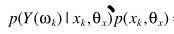 两个表达式,得出估计
两个表达式,得出估计

其中

与ML准则估计器中的思路一样,对Bessel近似处理
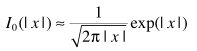
得出
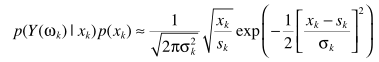
从而得出估计器
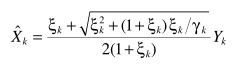
C-调参的建议
这一节是看到这里想到的,注意观察A、B两个估计器
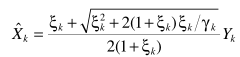
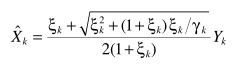
自己突发奇想,估计最多就水个水论文用得上,放在这里-感兴趣拿走。所以一个自然的思路是将他们推而广之:
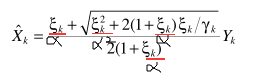
α是可以调节的参数。
ML、MMSE、MAP三种估计器:
1)其实ML可以理解成均匀分布的贝叶斯,这个时候的先验知识为零,通常贝叶斯假设高斯、拉普拉斯等分布(如幅值),这就引入了先验知识,如果这个先验知识有效,理论上效果应该比ML更好;这就像回归中的应用:无约束=均匀分布→最小二乘,高斯分布→Ridge回归,拉普拉斯分布→Lasso回归。
2)MMSE是基于统计平均的贝叶斯估计,注意它与Wiener是有区别的,虽然都基于均方误差最小准则;
3)MMSE找的是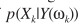 的均值,即
的均值,即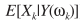 ,而MAP准则找的是
,而MAP准则找的是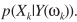 的最大值。
的最大值。
四、利用不存在概率 INCORPORATING SPEECH ABSENCE PROBABILITY IN SPEECH ENHANCEMENT
其实就是信息融合,也就是Boosting的思想:两个弱分类器,组合一个强分类器,两个弱增强器,组合一个强增强器。不多说了,不过书中将这点应用的还不够深入。

组合

关于此部分的更多内容参考这里。

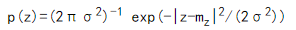

 浙公网安备 33010602011771号
浙公网安备 33010602011771号