Boosting学习笔记(Adboost、GBDT、Xgboost)
转载请注明出处:http://www.cnblogs.com/willnote/p/6801496.html
前言
本文为学习boosting时整理的笔记,全文主要包括以下几个部分:
- 对集成学习进行了简要的说明
- 给出了一个Adboost的具体实例
- 对Adboost的原理与学习过程进行了推导
- 针对GBDT的学习过程进行了简要介绍
- 针对Xgboost的损失函数进行了简要介绍
- 给出了Adboost实例在代码上的简单实现
文中的内容是我在学习boosting时整理的资料与理解,如果有错误的地方请及时指出,谢谢。
集成学习
集成学习通过构建并结合多个学习器来完成学习任务,有时也被称为多分类器系统、基于委员会的学习等。集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化性能。下面从两个方面对集成学习进行简要介绍。
-
分类
根据个体学习器的生成方式,目前的集成学习方法大致可以分为两大类,即个体学习器间存在强依赖关系、必须串行生成的序列化方法,以及个体学习器间不存在强依赖关系、可同时生成的并行化方法;前者的代表是Boosting,后者的代表是Bagging和随机森林。 -
结合策略
对于基分类器最终的结合策略常见的方法有如下几种:- 平均法
对于数值形输出,最常见的结合策略即为平均法:
\[H(x)=\frac{1}{T}\sum_{i=1}^{T}h_{i}(x) \]其中\(h_{i}(x)\)为基学习器的输出结果,\(H(x)\)为最终学习器的结果,\(T\)为基学习器的个数。
- 加权平均法
\[H(x)=\sum_{i=1}^{T}w_{i}h_{i}(x) \]其中\(w_{i}\)是个体学习器\(h_{i}\)的权重,通常要求\(w_{i}\geqslant 0,\sum_{i=1}^{T}w_{i}=1\)。显然,简单平均法是加权平均法令\(w_{i}=1/T\)的特例。
-
投票法
预测结果为得票最多的标记,若同时有多个标记获得相同的票数,则从中随机选取一个。 -
学习法
当训练数据很多时,可以通过另一个学习器来对所有基学习器产生结果的结合方法进行学习,这时候个体学习器称为初级学习器,用于结合的学习器成为次级学习器或元学习器。
- 平均法
Adaboost
思想
AdaBoost是最著名的Boosting族算法。开始时,所有样本的权重相同,训练得到第一个基分类器。从第二轮开始,每轮开始前都先根据上一轮基分类器的分类效果调整每个样本的权重,上一轮分错的样本权重提高,分对的样本权重降低。之后根据新得到样本的权重指导本轮中的基分类器训练,即在考虑样本不同权重的情况下得到本轮错误率最低的基分类器。重复以上步骤直至训练到约定的轮数结束,每一轮训练得到一个基分类器。
可以想象到,远离边界(超平面)的样本点总是分类正确,而分类边界附近的样本点总是有大概率被弱分类器(基分类器)分错,所以权值会变高,即边界附近的样本点会在分类时得到更多的重视。
举例
为了防止看到公式推导你(wo)就(zao)要(pao)跑(le),我们先来通过例子让你明白AdaBoost的运作方式,这样从整体框架上有个印象,之后再进行公式的推导。例子所用的代码在文章最后给出。
首先对一些符号进行约定:
| 符号 | 含义 |
|---|---|
| \(D = \{(\vec{x_{i}}, y_{i}),\ i\in[1, m]\}\) | 训练集,共m个样本 |
| \(T\) | 训练轮数 |
| \(D_{t}(x)\) | 第\(t\)轮时样本的权重分布 |
| \(h_{t}\) | 第\(t\)轮得到的基分类器 |
| \(\alpha_{t}\) | 第\(t\)轮得到的基分类器的权重 |
| \(\epsilon_{t}\) | 第\(t\)轮\(h_{t}\)的错误率 |
| \(P_{A}(D)\) | 强分类器\(A\)在数据集\(D\)上的最终准确率 |
接下来,给定下边的数据集\(D\),我们用AdaBoost算法来学习得到一个强分类器
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
数据集\(D\)共有10条数据,根据x的输入得到的y可以分类两类,即y=1与y=-1。我们每一轮使用最简单的决策树桩来构建基分类器,即每轮设定一个阈值\(\theta\),只要\(x<\theta\),就判定为正类(y=1),\(x>\theta\)就判定为负类(y=-1)。
第一轮
-
\(D_{1}(x)\)
因为是第一轮,故所有样本的权重相同:\[D_{1}(\vec{x})=\{\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10},\frac{1}{10}\} \] -
\(\theta\)
因为是离散数据,所以\(\theta\)可以依次取0.5,1.5,2.5,...,8.5来对x进行分类,这里可以有两种分类方法:- \(x<\theta\)时分为正类,\(x>\theta\)时分为负类,分类错误率对应\(\epsilon_{t}^{1}\)
- \(x>\theta\)时分为正类,\(x<\theta\)时分为负类,分类错误率对应\(\epsilon_{t}^{2}\)
最终要选择一个令\(\epsilon_{1}\)取得最小值的\(\theta\)与分类方法,这9个值在两种分类方法下,此层\(h_{1}\)的错误率\(\vec{\epsilon_{1}}\)分别为:
可以看到\(\vec{\epsilon_{1}^{1}}\)中的\(0.3*\frac{1}{10}\)为最小值。对应的,我们取\(\theta\)为2.5(\(\theta\)为8.5亦可),使用第一种分类方法。则x为0,1,2的样本分为正类,都分对了;而之后的样本都被分为负类,分错了3个,所以总错误率为\(3*\frac{1}{10}\)。故此轮弱分类器的阈值\(\theta\)取2.5,分类方法取第一种。
- \(\alpha_{1}\)
第一层基分类器\(h_{1}\)的权重\(\alpha_{1}\)的计算推到方法后面的推导部分再细说,此处只要知道通过如下的公式来计算即可:
- \(H(x), P_{A}(D)\)
根据如下公式计算\(H(x)\),此时\(T\)为1:
整个模型(现在只有一个基分类器)的准确率为:
至此第一轮的工作就结束了,可以看出被误分类样本的权值之和影响误差率,误差率影响基分类器在最终分类器中所占的权重。
第二轮
- \(D_{2}(x)\)
第一轮训练完成后对\(D_{1}(x)\)进行更新得到\(D_{2}(x)\),更新公式的推导过程也是等到后边的推到部分再说,此处还是只要知道通过下边的公式来计算更新即可:
上一轮中x=6、7、8的点分错了,可以看到这三个点在\(D_{2}\)中的权重变大了,而其余分类正确的点权重变小了。
- \(\theta\)
我们依然对\(\theta\)依次取0.5, 1.5, ... , 8.5来对x进行分类,注意我们刚才已经得到了\(D_{2}(x)\),样本权重的分布不再是第一轮全部相等的\(\frac{1}{10}\)了,如当\(\theta\)取0.5按第一种分类方法进行分类时,\(\epsilon_{2}^{1}\)计算方法如下:
对所有\(\theta\)与分类方法都按照如上的步骤进行计算,则可得到\(\vec{\epsilon_{2}^{1}}\)与\(\vec{\epsilon_{2}^{2}}\)分别为:
可以看到\(\vec{\epsilon_{2}^{1}}\)中的0.214为最小值,故此轮弱分类器的阈值\(\theta\)取8.5,分类方法为第一种。
- \(\alpha_{2}\)
依然使用如下公式进行计算:
- \(H(x), P_{A}(D)\)
继续根据如下公式计算\(H(x)\),此时\(T\)为2:
整个模型(现在有两个基分类器)的准确率仍然为:
至此第二轮的工作就结束了,下面我们继续使用上边的方式来看第三轮是否能将准确率提升。
第三轮
- \(D_{3}(x)\)
使用\(D_{2}(x)\)更新得到\(D_{3}(x)\)如下:
上一轮中x=3、4、5的点被分错,所以在\(D_{3}\)中的权重变大,其余分类正确的点权重变小。
- \(\theta\)
继续使用之前的方法得到\(\vec{\epsilon_{3}^{1}}\)与\(\vec{\epsilon_{3}^{2}}\)分别为:
可以看到\(\vec{\epsilon_{3}^{2}}\)中的0.182为最小值,故此轮弱分类器的阈值\(\theta\)取5.5,分类方法为第二种。
- \(\alpha_{2}\)
依然使用如下公式进行计算:
- \(H(x), P_{A}(D)\)
继续根据如下公式计算\(H(x)\),此时\(T\)为3:
整个模型(现在有三个基分类器)的准确率为:
至此,我们只用了3个弱(基)分类器就在样本集\(D\)上得到了100%的准确率,总结一下:
- 在第\(t\)轮被分错的样本,在下一轮更新得到的\(D_{t+1}(x)\)中权值将被增大
- 在第\(t\)轮被分对的样本,在下一轮更新得到的\(D_{t+1}(x)\)中权值将被减小
- 所使用的决策树桩总是选取让错误率\(\epsilon_{t}\)(所有被\(h_{t}\)分类错误的样本在\(D_{t}(x)\)中对应的权值之和)最低的阈值来设计基本分类器
- 最终Adboost得到的\(H(x)\)为:
其他情况
上边的例子每一轮使用了最简单的决策树桩来得到基分类器,下面就几种常见的其他情况对基分类器的训练过程进行简单介绍,纯粹个人理解,如有错误之处请及时指出。
- 分类问题
- 决策树桩
见上例 - 决策树
每一个节点的选择过程都需要将\(D_{t}(x)\)考虑进去,即在定义损失函数的时候,考虑每一个样本被分错的代价(权重) - 逻辑回归
阈值\(\theta\)的选取需令本层\(\epsilon_{t}\)取得最小值
- 决策树桩
- 回归问题
- 按照\(D_{t}(x)\)的分布对原始数据集进行重新采样,利用采样后得到的新数据集再进行训练
推导
AdaBoost算法可以认为是一种模型为加法模型、损失函数为指数函数、学习算法为前向分步算法的而分类学习方法。在对\(\alpha_{t}\)和\(D_{t}\)进行推导前,我们先对加法模型和前向分步算法进行简要介绍。
- 加法模型
加法模型的定义如下:
其中,\(b(x;\gamma_{m})\)为基函数,\(\beta_{m}\)为基函数的系数,\(\gamma_{m}\)为基函数的参数。在给定训练数据及损失函数\(L(y, f(x))\)的条件下,学习加法模型\(f(x)\)成为经验风险极小化,即损失函数极小化的问题:
这通常是一个极其复杂的优化问题,因为需要同时考虑所有基函数与其权重的选取来令目标最小化。
- 前向分步算法
前向分步算法对加法模型的求解思路是:如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近优化目标,那么就可以简化优化的复杂度。即每步只需优化如下损失函数:
这样,前向分步算法将同时求解所有步骤的\(\beta_{m}\)、\(\gamma_{m}\)的优化问题简化为逐次求解各个\(\beta_{m}\)、\(\gamma_{m}\)的优化问题。
- \(\alpha_{t}\)的推导过程
AdaBoost算法是前向分布加法算法的特例。这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。即此时的基函数为基分类器。AdaBoost的最终分类器为:
损失函数为:
上式即被称为指数损失函数,其中y是样本的真实类别。假设在第t轮迭代时有:
目标是使得到的\(\alpha_{t}\)和\(h_{t}(x)\)令\(L(y, H(x))\)最小,即:
其中,\(\bar{w}_{ti}=e^{-y_{i}H_{t-1}(x)}\)。因为\(\bar{w}_{ti}\)既不依赖于\(\alpha_{t}\)也不依赖于\(h_{t}(x)\),所以与最小化无关。但它依赖于\(H_{t-1}(x)\),会随着每一轮迭代而发生变化。第二个式子为令指数损失函数最小的\(h_{t}(x)^{*}\),其中\(I(\cdot)\)为指示函数,此\(h_{t}(x)^{*}\)使第m轮加权训练数据分类的误差率得到了最小值。接下来我们对上边的第一个式子的右边进行一下简单变形:
将上式对\(\alpha_{t}\)求导并令导数为0,即可解得:
上式即之前例子中所用到的\(\alpha_{t}\)的更新公式,其中,\(e_{t}\)为分类误差率:
由此可知,当\(e_{t}\leqslant \frac{1}{2}\)时,\(\alpha_{t}\geqslant 0\),并且\(\alpha_{t}\)随着\(e_{t}\)的减小而增大,所以分类误差率越小的基分类器在最终分类器中的作用越大。
- \(D_{t}\)的推导过程
接下来我们对\(D_{t}\)的更新公式进行推导。由之前推导过程中所得到的下边两个式子:
将第一个式子两边同乘\(-y_{i}\),并作为\(e\)的指数即可得到下一轮\(\bar{w}_{t+1,i}\)的更新公式:
上式再在分母添加一个规范化因子即为例子中所用到的\(D_{t}\)的更新公式。
总结
在训练过程中,每个新的模型都会基于前一个模型的表现结果进行调整,这也就是为什么AdaBoost是自适应(adaptive)的原因,即AdaBoost可以自动适应每个基学习器的准确率。
GBDT
-
简介
GBDT即梯度提升树,提升方法依然采用的是加法模型与前向分布算法。以决策树为基函数的提升方法称为提升树。对分类问题决策树是二叉分类树,对回归问题决策树是二叉决策树。例如前文中的例子中所使用的决策树桩即为一个根节点直接连接两个叶节点的简单决策树。 -
与Adboost的区别
GBDT与Adboost最主要的区别在于两者如何识别模型的问题。Adaboost用错分数据点来识别问题,通过调整错分数据点的权重来改进模型。GBDT通过负梯度来识别问题,通过计算负梯度来改进模型。 -
学习过程
针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。包括用平方误差损失函数的回归问题,是指数损失函数的分类问题,以及用一般损失函数的一般决策问题。对于分类问题,GBDT实质是把它转化为回归问题。在多分类问题中,假设有k个类别,那么每一轮迭代实质是构建了k棵树,对某个样本x的预测值为
之后使用softmax可以得到属于每一个类别的概率,此时该样本的loss即可以用logitloss来表示,并对所有类别的f(x)都可以算出一个梯度,即可以计算出当前轮的残差,供下一轮迭代学习。下面主要对回归问题的提升树进行说明。
依然采用前向分步算法,过程如下:
$$f_{0}(x)=0\\
f_{m}(x)=f_{m-1}(x)+T(x;\Theta), m=1,2,...,M\\
f_{M}(x)=\sum_{m=1}^{M}T(x;\Theta_{m})$$
第一个式子首先定义初始提升树$f_{0}(x)=0$;之后第m步的模型即为第二个式子,其中$T(x;\Theta)$表示决策树,$\Theta$为决策树的参数;第三个式子表示GBDM的最终模型,其中M为树的个数。
在前向分步算法的第m步,给定当前模型$f_{m-1}(x)$,需求解
$$\hat{\Theta}_{m}=\underset{\Theta_{m}}{arg\ min}\sum_{i=1}^{N}L(y_{i},f_{m-1}(x_{i})+T(x_{i};\Theta_{m}))$$
得到的$\hat{\Theta}_{m}$即为第m颗树的参数。当采用平方误差作为损失函数时:
$$L(y,f(x))=(y-f(x))^{2}$$
带入上式中,则其损失函数变为:
$$L(y,f_{m-1}(x)+T(x;\Theta_{m}))\\
=[y-f_{m-1}(x)-T(x;\Theta_{m})]^{2}\\
=[r-T(x;\Theta_{m})]^{2}$$
这里
$$r=y-f_{m-1}(x)$$
是当前模型拟合数据的残差。所以,对于回归问题的提升树算法来说,只需简单地拟合当前模型的残差。即每一轮产生的残差作为下一轮回归树的输入,下一轮的回归树的目的就是尽可能的拟合这个输入残差。
-
举例
我们以简单的年龄预测为例,训练集共包括4个人:A,B,C,D,他们的年龄分别是14,16,24,26。每个人都有两个属性:每周的购物金额、每周的上网时间。数据集如下:- A:购物金额<=1K,上网时间<=20h
- B:购物金额<=1K,上网时间>=20h
- C:购物金额>=1K,上网时间<=20h
- D:购物金额>=1K,上网时间>=20h
我们的目的就是构建一个GBDT模型来预测年龄。简单起见,我们限定每棵树只有一个分支,如下图所示:

- 第一轮(树)
第一颗树节点属性的选取我们用最小化残差的方法。当选择每周购物金额作为划分属性时,两边叶子节点的残差和为:
当选择上网时间作为划分属性时,得到的残差和为:
通过比较上边两种方法,我们选择每周的购物金额作为划分属性,结果如上图左边的树。此时可以看到A、B被划分到了左节点。左节点的均值为(14+16)/2=15,则A的残差为14-15=-1,B的残差为16-15=1,同理可得C和D的残差分别为-1和1。这样当4个样本经过第一颗树后,分别产生的残差为(-1,1,-1,1),这个残差作为第二课树的输入,如上图右边第二颗树的根节点。
-
第二轮(树)
第二颗树的目的是尽量去拟合由第一颗树产生的残差(-1,1,-1,1),特征选取的过程同第一棵树,不再复述。现在我们用每周的上网时间来作为划分的属性,则结果如上图第二颗树。A、C被划分到左节点,B、D被划分到右节点,两个节点的均值分别为-1和1。此时两个子节点的残差都为0,训练结束。 -
结果
不考虑泛化性,我们简单地使用训练集进行测试。
A = 15 + (–1) = 14
B = 15 + 1 = 16
C = 25 + (–1) = 24
D = 25 + 1 = 26
全部预测正确,厉(fei)害(hua)了我的哥。 -
总结
- GBDT每一轮训练时所关注的重点是本轮产生结果的残差,下一轮以本轮残差作为输入,尽量去拟合这个残差,使下一轮输出的残差不断变小。所以GBDT可以做到每一轮一定向损失函数减小的梯度方向变化,而传统的boosting算法只能是尽量向梯度方向减小,这是GBDT与传统boosting算法最大的区别,这也是为什么GBDT相比传统boosting算法可以用更少的树个数与深度达到更好的效果。
- 和AdaBoost一样,Gradient Boosting也是重复选择一个表现一般的模型并且每次基于先前模型的表现进行调整。不同的是,AdaBoost是通过提升错分数据点的权重来定位模型的不足,而GBDT是通过算梯度来定位模型的不足。因此相比AdaBoost,GBDT可以使用更多种类的目标函数。
- 抽象地说,模型的训练过程是对一任意可导目标函数的优化过程,通过反复地选择一个指向负梯度方向的函数,该算法可被看作在函数空间里对目标函数进行优化。
- 回归问题
- 用回归树去拟合残差,其实就是用回归树去拟合目标方程关于f(x)的梯度。
- 回归的目标函数并不一定会用square loss。square loss的优点是便于理解和实现,缺点在于对于异常值它的鲁棒性较差,一个异常值造成的损失由于二次幂而被过分放大,会影响到最后得到模型在测试集上的表现。可以算则Absolute loss或者Huber loss代替。
- 分类问题
- 此时的目标函数常用log loss,如KL-散度或者交叉熵。
- 除了损失函数的区别外,分类问题和回归问题的区别还在于当多分类问题时,每轮可能会训练多个分类器。
- 由于决策树是非线性的,并且随着深度的加深,非线性越来越强,所以基于决策树的GBDT也是非线性的。
xgboost
-
简介
xgboost 的全称是eXtreme Gradient Boosting,由华盛顿大学的陈天奇博士提出,在Kaggle的希格斯子信号识别竞赛中使用,因其出众的效率与较高的预测准确度而引起了广泛的关注。 -
与Adboost的区别
GBDT算法只利用了一阶的导数信息,xgboost对损失函数做了二阶的泰勒展开,并在目标函数之外加入了正则项对整体求最优解,用以权衡目标函数的下降和模型的复杂程度,避免过拟合。所以不考虑细节方面,两者最大的不同就是目标函数的定义,接下来就着重从xgboost的目标函数定义上来进行介绍。 -
目标函数
xgboost的目标函数定义如下:
其中,t表示第t轮,\(f_{t}\)表示第t轮所生成的树模型,\(\Omega(f_{i})\)表示正则项,\(constant=\sum_{i=1}^{t-1}\Omega(f_{i})\)。接下来是xgboost的重点,我们使用泰勒展开
来定义一个近似的目标函数如下:
因为\(l(y_{i},\hat y_{i}^{(t-1)})\)的值由之前的过程决定,所以本轮不变,\(constant\)也不影响本轮的训练,所以将这两者其去掉,得到:
现在的目标函数有一个非常明显的特点,它只依赖于每个数据点在误差函数上的一阶导数和二阶导数。接下来,我们对\(f_{t}\)的定义做一下细化,将树拆分成结构部分\(q\)和叶子权重部分\(w\):
当我们给定了如上定义之后,就可以对树的复杂度\(\Omega(f_{t})\)进行定义了:
其中,第一部分中的T为叶子的个数,第二部分为\(w\)的L2模平方。我们来看下图的示例:
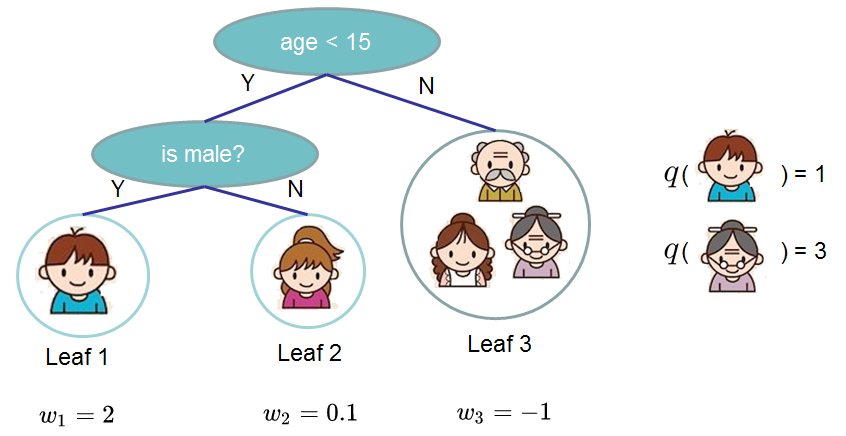
可以看到叶子的权重\(w\)就是GBDT例子中叶子结点的值,而\(q\)就是将某个样本点映射到某个叶子结点的函数。有了上边的两个式子后,继续对目标函数进行如下改写:
其中,\(I_{j}\)为每个叶子节点上的样本集合\(I_{j}=\{i|q(x_{i}=j\}\)。现在这个目标函数包含了T个相互独立的单变量二次函数,我们定义:
那么我们就得到了最终的目标函数样子:
现在我们假设\(q\)已知,通过将上式对\(w\)求导并令其等于0,就可以求出令\(Obj^{(t)}\)最小的\(w\):
剩下的工作就很简单了,通过改变树的结构来找到最小的\(w_{j}^{*}\),而对应的结构就是我们所需要的结果。不过枚举所有树的结构不太可行,所以常用的是贪心法,每一次尝试去对已有的叶子加入一个分割。对于一个具体的分割方案,我们可以获得的增益可以由如下公式计算:
观察这个目标函数会发现如下三点:
-
这个公式形式上跟ID3算法(采用entropy计算增益) 、CART算法(采用gini指数计算增益) 是一致的,都是用分裂后的某种值减去分裂前的某种值,从而得到增益
-
引入分割不一定会使情况变好,因为最后有一个新叶子的惩罚项。所以这也体现了预减枝的思想,即当引入的分割所带来的增益小于一个阈值时,就剪掉这个分割
-
上式中还有一个系数\(\lambda\),是正则项里\(w\)的L2模平方的系数,对\(w\)做了平滑,也起到了防止过拟合的作用,这个是传统GBDT里不具备的特性
-
总结
xgboost与传统的GBDT相比,对代价函数进行了二阶泰勒展开,同时用到了一阶与二阶导数,而GBDT在优化时只用到一阶导数的信息,个人认为类似牛顿法与梯度下降的区别。另一方面,xgboost在损失函数里加入的正则项可用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出score的L2模的平方和。从Bias-variance tradeoff角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合,这也是xgboost优于传统GBDT的一个特性。
代码
针对上文Adboost中使用决策树桩作为基分类器的例子写了一个简单实现,类Adboost中的方法__get_decision_stump()为决策树桩,大家可以另写一个其他算法的实现进行替换,之后对train()方法重写以完成自己想要的训练步骤与每轮的打印信息,其他部分参照代码注释。
import math
class Adboost(object):
def __init__(self, x_list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
y_list = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]):
"""initialization
initializing parameters of the Adboost
input
x_list : training data set
y_list : labels of the x_list
"""
self.x_list = x_list
self.y_list = y_list
self.sample_count = len(self.y_list)
self.dt_list = [0.1] * self.sample_count #the distribution of sample weights in the current round
self.dt_next_list = [] #the distribution of sample weights in the next round
self.ht_list = [] #results of the base classifier in the current round
self.alpha = 0.0 #the weight of the self.ht_list
self.Ht_list = [0.0] * self.sample_count #results of the Adboost in the current round
self.Ht_sign_list = [] #sign(self.Ht_list)
self.acc = 0.0 #the accuracy rate of the Adboost in the current round
def __get_decision_stump(self):
"""base classifier(decision stump)
obtain the decision stump by minimizing the classification error of current round with the self.dt_list
output
error_list : the error of each theta value and method
method_flag : method flag
error_min : the minimum error of the error_list
theta_min : the value of theta of the corresponding error_min
error_min is necessary for return to compute other parameters, the rest are not
"""
def __get_ht_list(theta):
ht_list = []
for x in self.x_list:
if x < theta:
ht_list.append(1)
else:
ht_list.append(-1)
return ht_list
theta_list = [x + 0.5 for x in self.x_list[:-1]]
error_list = [[], []]
error_min = 99999
for theta in theta_list:
ht_list_1 = __get_ht_list(theta) #method 1
ht_list_2 = [-ht for ht in ht_list_1] #method 2
for method, ht_list in enumerate([ht_list_1, ht_list_2]):
error = 0
for loc, y_ in enumerate(ht_list):
if y_ != self.y_list[loc]:
error += self.dt_list[loc]
error_list[method].append(error)
if error < error_min:
error_min = error
theta_min = theta
method_flag = method + 1
self.ht_list = ht_list
return error_list, method_flag, error_min, theta_min
def __get_alpha(self, error):
self.alpha = 0.5 * math.log((1-error)/(error))
def __get_dt_next(self):
for loc, dt in enumerate(self.dt_list):
z = math.e**(-self.alpha * self.y_list[loc] * self.ht_list[loc])
self.dt_next_list.append(dt * z)
self.dt_next_list = [dt / sum(self.dt_next_list) for dt in self.dt_next_list]
def __get_acc_rate(self):
error = 0
for loc, _ in enumerate(self.x_list):
self.Ht_list[loc] += self.alpha * self.ht_list[loc]
self.Ht_sign_list = [int(math.pow(-1, (Ht > 0) * 1 + 1)) for Ht in self.Ht_list]
self.acc = map(cmp, self.Ht_sign_list, self.y_list).count(0) / (self.sample_count + 0.0)
def train(self, T = 3):
for t in range(T):
error_list, method, error, theta = self.__get_decision_stump()
self.__get_alpha(error)
self.__get_dt_next()
self.__get_acc_rate()
print '--------------Round %s--------------' % (t+1)
print 'error list : %s\n\t\t\t %s' % ([round(e, 3) for e in error_list[0]],\
[round(e, 3) for e in error_list[1]])
print 'theta : %s' % theta
print 'method : %s' % method
print 'error : %s' % round(error, 4)
print 'alpha : %s' % round(self.alpha, 4)
print 'ht_list : %s' % self.ht_list
print 'dt_list : %s' % [round(dt, 3) for dt in self.dt_list]
print 'dt_next_list : %s' % [round(dt, 3) for dt in self.dt_next_list]
print 'Ht_list : %s' % [round(Ht, 3) for Ht in self.Ht_list]
print 'Ht_sign_list : %s' % self.Ht_sign_list
print 'accuracy rate : %s' % self.acc
print '------------------------------------\n'
self.dt_list = self.dt_next_list
self.dt_next_list = []
if self.acc == 1.0:
break
if __name__ == "__main__":
adb = Adboost()
adb.train(5)
----------------------------------------Output----------------------------------------
--------------Round 1--------------
error list : [0.5, 0.4, 0.3, 0.4, 0.5, 0.6, 0.5, 0.4, 0.3]
[0.5, 0.6, 0.7, 0.6, 0.5, 0.4, 0.5, 0.6, 0.7]
theta : 2.5
method : 1
error : 0.3
alpha : 0.4236
ht_list : [1, 1, 1, -1, -1, -1, -1, -1, -1, -1]
dt_list : [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]
dt_next_list : [0.071, 0.071, 0.071, 0.071, 0.071, 0.071, 0.167, 0.167, 0.167, 0.071]
Ht_list : [0.424, 0.424, 0.424, -0.424, -0.424, -0.424, -0.424, -0.424, -0.424, -0.424]
Ht_sign_list : [1, 1, 1, -1, -1, -1, -1, -1, -1, -1]
accuracy rate : 0.7
------------------------------------
--------------Round 2--------------
error list : [0.643, 0.571, 0.5, 0.571, 0.643, 0.714, 0.548, 0.381, 0.214]
[0.357, 0.429, 0.5, 0.429, 0.357, 0.286, 0.452, 0.619, 0.786]
theta : 8.5
method : 1
error : 0.2143
alpha : 0.6496
ht_list : [1, 1, 1, 1, 1, 1, 1, 1, 1, -1]
dt_list : [0.071, 0.071, 0.071, 0.071, 0.071, 0.071, 0.167, 0.167, 0.167, 0.071]
dt_next_list : [0.045, 0.045, 0.045, 0.167, 0.167, 0.167, 0.106, 0.106, 0.106, 0.045]
Ht_list : [1.073, 1.073, 1.073, 0.226, 0.226, 0.226, 0.226, 0.226, 0.226, -1.073]
Ht_sign_list : [1, 1, 1, 1, 1, 1, 1, 1, 1, -1]
accuracy rate : 0.7
------------------------------------
--------------Round 3--------------
error list : [0.409, 0.364, 0.318, 0.485, 0.652, 0.818, 0.712, 0.606, 0.5]
[0.591, 0.636, 0.682, 0.515, 0.348, 0.182, 0.288, 0.394, 0.5]
theta : 5.5
method : 2
error : 0.1818
alpha : 0.752
ht_list : [-1, -1, -1, -1, -1, -1, 1, 1, 1, 1]
dt_list : [0.045, 0.045, 0.045, 0.167, 0.167, 0.167, 0.106, 0.106, 0.106, 0.045]
dt_next_list : [0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125]
Ht_list : [0.321, 0.321, 0.321, -0.526, -0.526, -0.526, 0.978, 0.978, 0.978, -0.321]
Ht_sign_list : [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]
accuracy rate : 1.0
------------------------------------




 浙公网安备 33010602011771号
浙公网安备 33010602011771号