部分排序算法的介绍及实现
算法要考试了，复习到了排序的知识，所以对复习的内容进行以下总结，参考书目《算法导论》。排序问题是算法与数据结构中常讲到的问题了，有次面试问到了具体的快速排序的原理以及实现，顿时当时就愣了，平时各种语言提供的类库中都有实现好的快速排序算法，针对这个算法原理也就没有在意；不过这次算法课程结束了感觉算法内容还是挺重要的，不过参考算法导论的话真的学了好多数学知识，也被许多数学知识给吓住了，算法导论一书重点不在于算法的实践，经典的算法只是给出了伪代码，然后大量的篇幅进行正确性证明，复杂度分析，胡言乱语一番，接下来具体算法的介绍啦。
1、插入排序
插入排序的原理是访问过的部分是有序的，不过只记住原理有时候是写不出代码的，或者有了代码看不出它的这个原理，说这句是因为我记得以前考软考的时候一个变换了一下的插入排序的伪代码放在我的面前，我竟然不认识它...话不多说，直接上代码
bool insertSort(unsigned int* array,int length)
{
int i,j;
unsigned int k;
for (i=1;i<length;i++)
{
j = i - 1;
//把第i个元素先拿出来，比它大的依次向后挪动，然后把它插到j+1的位置上，刚好j+1的元素挪动到j上了
key = array[i];
//比key大的都向后挪动
while (j>=0&&key < array[j])
{
array[j+1] = array[j];
j--;
}
array[j+1] = key;
}
return true;
}
插入排序实际应用中也不经常用到，不过有些还是会用到的，比如数据量比较小的情况下，插入排序是最快的，所以有的算法的在小的规模会利用这种暴力法，我对插入排序比较敬畏就是因为那次软考中看不出插入排序，当时真是太年轻了，时间复杂度O（n2），插入排序一般情况下也是稳定的排序算法。
2、归并排序
好像说外排序的原理和归并排序差不多，不过我还是没有实现过，这里的排序算法都是内存排序算法了，归并排序需要开辟一个额外的内容空间，但是时间复杂度为Θ（nlgn），虽说这是一个Θ，但是后面会看到，实际应用中它不如快速排序快速，后面会分析下原因的，归并排序一般情况属于稳定的排序算法，这个算法思想比较简单，而且上篇日志分治算法中介绍了，主要工作在于merge中，直接贴代码了
bool PreMergeSort(unsigned int* array,int begin,int end)
{
unsigned int* arrayAssit = new unsigned int[end - begin + 1];
mergeSort(array,arrayAssit,begin,end);
delete [] arrayAssit;
return true;
}
bool mergeSort(unsigned int* array,unsigned int* arrayAssit,int begin,int end)
{
if (end == begin)
{
return true;
}
int mid = (begin+end)/2;
mergeSort(array,arrayAssit,begin,mid);
mergeSort(array,arrayAssit,mid+1,end);
merge(array,arrayAssit,begin,mid,end);
return true;
}
bool merge(unsigned int* array,unsigned int* arrayAssit,int begin,int mid,int end)
{
int i,j,k;
i = begin;
j = mid + 1;
k = begin;
while(i <= mid&&j<= end)
{
if (array[i] <= array[j])
{
arrayAssit[k++] = array[i++];
}
else
{
arrayAssit[k++] = array[j++];
}
}
while (i <= mid)
{
arrayAssit[k++] = array[i++];
}
while (j <= end)
{
arrayAssit[k++] = array[j++];
}
memcpy(array+begin,arrayAssit+begin,(end-begin+1)*sizeof(array[0]));
return true;
}
分治算法设计的思想很重要的，接下来的快速排序算法也是基于分治的思想...
3、快速排序
快速排序是面试中经常出现的问题呀，所以了解其原理，熟练写出伪代码还是必备技能呀，会写一个冒泡和插入是不行的，记忆快速排序的方法是其是一个不需要额外空间的排序算法，又称原地排序，不需要归并排序中那样数组的复制什么的。主要原理就是找一个分割元素，把数组分成左边和右边，然后递归，快速排序一般情况下是不稳定的排序算法，直接贴3种快速排序的算法，哪一种容易记忆挑哪一种呀~不过性能最好的是三数取中是性能最好的啦，不过复杂了一点，
（1）算法导论中每次取最后元素作为分割元素
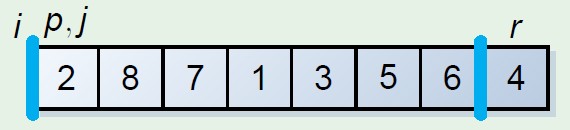
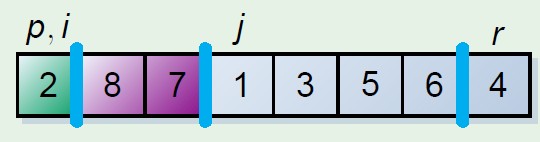
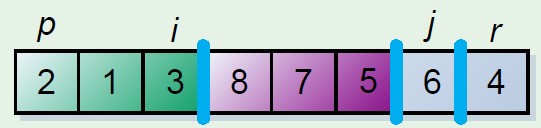
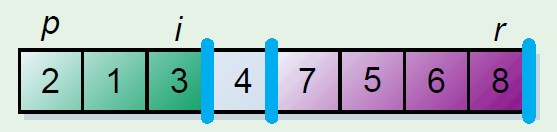
这个分割数组的原理保留两个指示器元素，i，j，其中一个，假如为i是遍历元素的指示器，另外一个指示器保留的位置是其前面的元素均小于分割元
步骤是i和j初始化相同的位置，起始坐标，i向后遍历，遇到小于分割元素的时候，此时更换当前元素和j元素指示位置，j++，这时候j前面就是小于分割元素的元素，最后结束的时候将分割元素和j的元素更换，则分割元素放到中间位置
bool swap(unsigned int& i,unsigned int& j)
{
unsigned int tmp;
tmp = i;
i = j;
j = tmp;
return true;
}
unsigned int partitionLast(unsigned int* array,int begin,int end)
{
unsigned int divide = array[end];
int i = begin - 1;
int j;
for (j = begin;j < end;j++)
{
if (array[j]<divide)
{
i++;
swap(array[i],array[j]);
}
}
swap(array[i+1],array[end]);
return i+1;
}
bool quickSortLast(unsigned int* array,int begin,int end)
{
unsigned int divide;
if (begin<end)
{
divide = partitionLast(array,begin,end);
quickSortLast(array,begin,divide-1);
quickSortLast(array,divide+1,end);
}
return true;
}
（2）每次取第一个元素作为分割元素，好像是叫霍尔(Hore)排序
这个方法不同于第一个方法，没有分割出来具体的分割部分，原理如下：
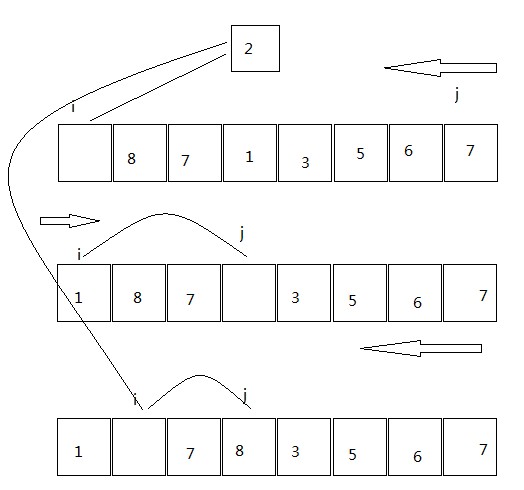
首先拿出第一个元素作为分割元素。此时第一个元素是可复写的状态，所以此时从后面遍历，找到第一个小于分割元素的元素，复写第一个元素，此时它是可复写状态，j保留了它的位置，所以这时候利用i从前面遍历，找到第一个大于分割元素的元素，复写j的状态，然后在从j进行，如此交替直到i=j的时候，这时候此位置的元素为可复写状态，分割元素填入及分割完毕，接下来递归调用
bool quickSortFirst(unsigned int* array,int begin,int end)
{
int i,j;
unsigned int divide = array[begin];
i = begin;
j = end;
while (i<j)
{
while (i<j&&array[j]>=divide)
j--;
array[i] = array[j];
while (i<j&&array[i]<=divide)
i++;
array[j] = array[i];
}
array[i]=divide;
if (i-1 > begin)
quickSortFirst(array,begin,i-1);
if (i+1 < end)
quickSortFirst(array,i+1,end);
return true;
}
（3）三数取中快速排序实现
这个方法更加仔细的选择分割元素，这个方法在选分割元素的时候是比较开始元素，末尾元素，中间元素的大小，然后选取中间大小的元素，并且将其和倒数第二个元素交换，这样末尾元素和开始元素已经在两边了，提升了一些效率，避免了最坏情况，这种方法效率比较高。
unsigned int selectThreeDivide(unsigned int* array,int begin,int end)
{
int mid = (end+begin)/2;
if (array[begin]>array[mid])
swap(array[begin],array[mid]);
if (array[begin]>array[end])
swap(array[begin],array[end]);
if (array[mid]>array[end])
swap(array[mid],array[end]);
swap(array[mid],array[end-1]);
return array[end-1];
}
bool quickSortThree(unsigned int* array,int begin,int end)
{
int i,j;
unsigned int divide = selectThreeDivide(array,begin,end);
i = begin;
j = end - 1;
while (i<j)
{
while (i<j&&array[i]<=divide)
i++;
array[j] = array[i];
while (i<j&&array[j]>=divide)
j--;
array[i] = array[j];
}
array[i] = divide;
if (i-1>begin)
quickSortThree(array,begin,i-1);
if (i+1<end)
quickSortThree(array,i+1,end);
return true;
}
快速排序时间复杂度分析：
快速排序的时间复杂度分析也比较复杂，不过针对有序的元素应用上面的固定选择分割元素的时候会达到最坏的情况，最坏的情况就是每次分割的时候有一边没有元素，这样时间复杂度就是O（n2），不过实际应用中很少针对已经有序的数组进行排序，
不过快速排序针对这个方法有随机化的方法，每次随机选取分割元素。这样即可存在最坏情况交叉，也总能够得到好的情况。
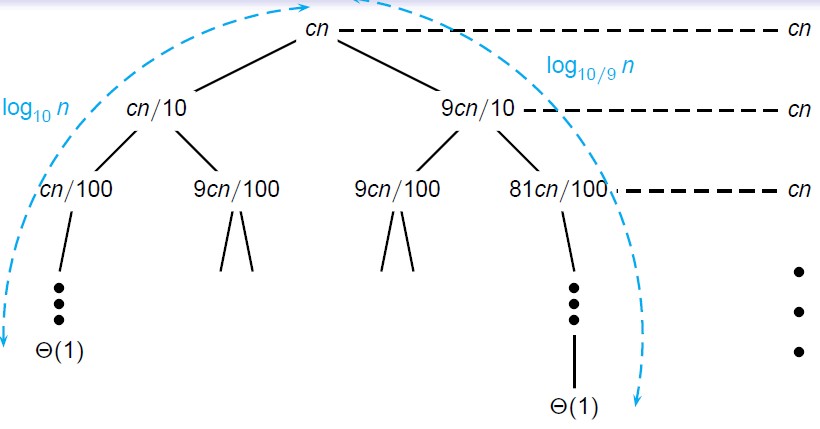
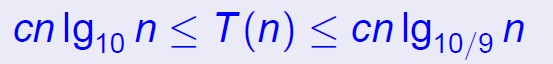
仍然属于Θ（nlgn）的范围。
随机化快速排序的分析需要利用随机化的分析方法，引入随机指示器变量，针对时间复杂度求期望，数学证明比较复杂，这里略去。了解随机化快速排序的时间复杂度为Θ（nlgn）即可。
快速排序效率较高的原因其中之一是缓存命中率较高，不需要频换的调换缓存，这个因素还会影响后面基数排序效率的测试~
基于比较排序的下限：
基于比较排序下限的证明是通过决策树证明的，决策树的高度Ω（nlgn），这样就得出了比较排序的下限。
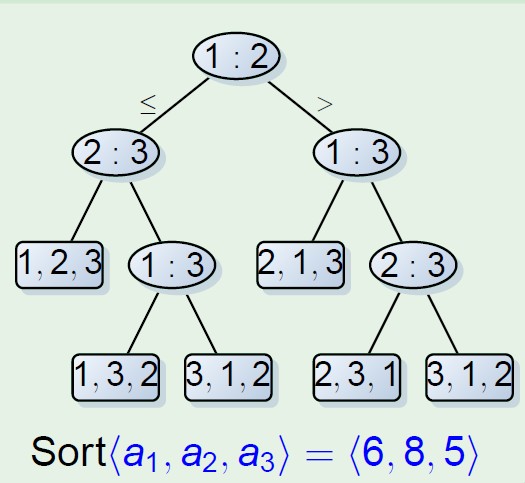
证明方法是每次比较排序均需要至叶节点算排序结束，然而n个元素共有n！个叶节点，根据二叉树的性质可知高度h的叶节点个数最多等于2h，h>=lg(n!)，且n！改写为（n/e）n，所以h>=nlgn-nlge,所以下限是nlgn
由于基于比较的下限是nlgn，所以针对快速排序等一些排序算法已经能够达到好的结果，时间复杂度明显提高不太可能了，所以下面介绍一些非比较排序，有些能够达到线性的时间。
1、计数排序
下面的代码是基数排序中计数排序的部分
bool countSort(radixSortNum* array,radixSortNum* arrayAssit,int* arrayCount,int length,int k)
{
int i;
for (i = 0;i<k;i++)
{
arrayCount[i] = 0;
}
for (i = 0;i<length;i++)
{
arrayCount[array[i].forCountSort]++;
}
for (i = 0;i<k-1;i++)
{
arrayCount[i+1]+=arrayCount[i];
}
for (i = length-1;i>=0;i--)
{
arrayAssit[arrayCount[array[i].forCountSort]-1].forCountSort = array[i].forCountSort;
arrayAssit[arrayCount[array[i].forCountSort]-1].src = array[i].src;
arrayCount[array[i].forCountSort]--;
}
memcpy(array,arrayAssit,(length)*sizeof(array[0]));
return true;
}
这种排序方法一般情况是稳定的排序方法，所以能够利用在基数排序中，基数排序要求的子排序部分是稳定的排序方法。
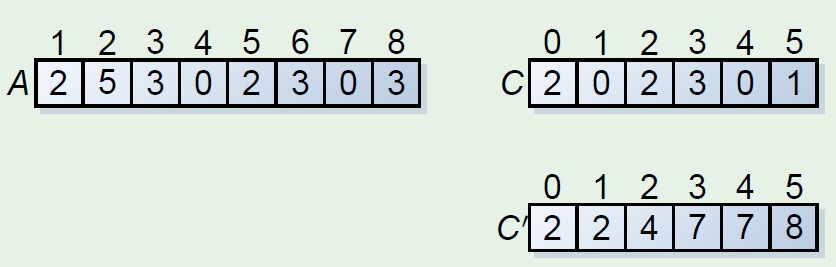
计数排序预先处理成如下的结构，C‘中保存的元素及为每个元素的位置，直接可输出。如下，看了图应该就知道原理了吧，具体C中就是保留了B中元素的应该输出的位置信息。该排序方法适合排序的范围k比较小
2、基数排序
基数排序中稳定的排序算法使用的是计数排序，关于基数算法的实现的讨论主要是r 值取多少才能保证效率的最高。书上给出了排序的时间复杂度公式 
，因此书上给出了理论上的r 的最合理的值为lg(n)。但是实验对这个r 值的选取进行了测试，发现实际情况并不是lg(n)使得算法达到最优，具体r 值的选取参见性能比较的结论。 这里取的每段r 值的大小的时候用位操作，相比%更加有效率。
bool PrecountSort(radixSortNum* array,int length,int k)
{
radixSortNum* arrayAssit = new radixSortNum[length];
int* arrayCount = new int[k];
countSort(array,arrayAssit,arrayCount,length,k);
delete [] arrayAssit;
delete [] arrayCount;
return true;
}
bool countSort(radixSortNum* array,radixSortNum* arrayAssit,int* arrayCount,int length,int k)
{
int i;
for (i = 0;i<k;i++)
{
arrayCount[i] = 0;
}
for (i = 0;i<length;i++)
{
arrayCount[array[i].forCountSort]++;
}
for (i = 0;i<k-1;i++)
{
arrayCount[i+1]+=arrayCount[i];
}
for (i = length-1;i>=0;i--)
{
arrayAssit[arrayCount[array[i].forCountSort]-1].forCountSort = array[i].forCountSort;
arrayAssit[arrayCount[array[i].forCountSort]-1].src = array[i].src;
arrayCount[array[i].forCountSort]--;
}
memcpy(array,arrayAssit,(length)*sizeof(array[0]));
return true;
}
bool radixSort(radixSortNum* array,int length,int numlen,int r)
{
bitset<32> bitmode(0x0000);
int i;
if (r == 0)
r = (int)(log(double(length))/log((double)2));
cout<<"r:"<<r<<endl;
for (i = 0;i < r;i++)
{
bitmode[i] = 1;
}
unsigned int mode = bitmode.to_ulong();
//cout<<mode<<endl;
//cout<<bitmode<<endl;
numlen = 32;
int leftLen = (int)ceil((double)numlen/(double)r),j=0;
leftLen +=1;//尽量多挪动一次，后面超过31就退出循环；
//cout<<"需要挪动这么多次:"<<leftLen<<endl;
//cout<<"mode:"<<bitmode<<endl;
while (leftLen > 0)
{
if (j*r>31)
{
break;
}
for (i = 0;i<length;i++)
{
unsigned int tmp = array[i].src>>(j*r);
//bitset<32> bittmp(tmp);
//cout<<"time:"<<j+1<<"bitset:"<<bittmp<<endl;
array[i].forCountSort = (tmp)&mode;
}
PrecountSort(array,length,(int)pow((double)2,r));
j++;
leftLen--;
}
return true;
}
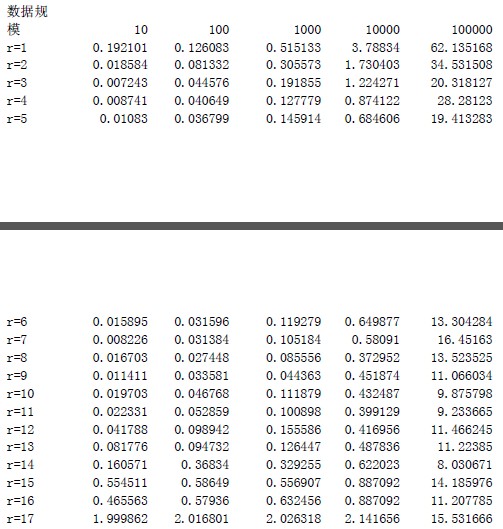
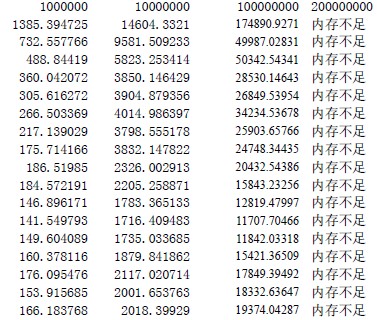
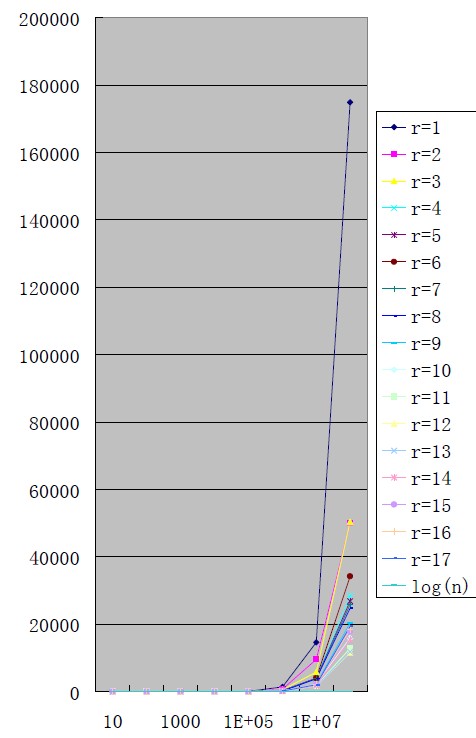
根据实验表明，这里的R 与理论值有差别，R 值取12 的时候达到最高的效率，为什么跟理论值有偏差呢？这里考虑可能与CACHE 有关，因为R 取12 的时候，刚好基数排序里面的计数排序部分能够在CACHE 中完成，所以效率最高。
3、桶排序
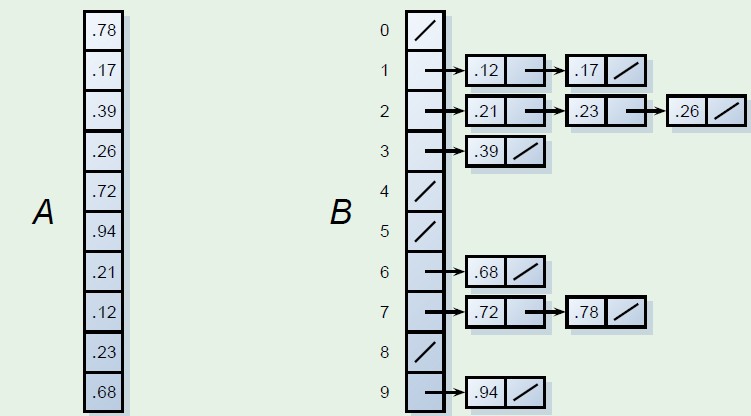
最好的元素一个元素对应一个坑位。
最后贴一个一些排序算法效率的比较
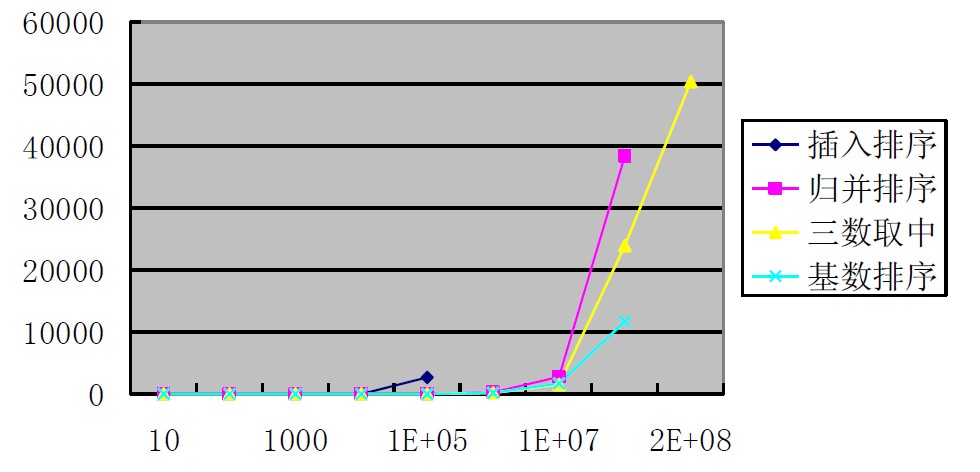
基数排序效率虽然较高，但是有一定的局限性，实现相对快速排序难度大一些，需要额外的空间，所以实际选择中快速排序选择比较多。
文章本意做复习笔记和分享用途，转载请标明出处，谢谢~
