Functional Programming without Lambda - Part 1 Functional Composition

Functions in Java

Prior to the introduction of Lambda Expressions feature in version 8, Java had long been known as a purely object-oriented programming language. "Everything is an Object" is the philosophy deep in the language design. Objects are entities with identity, states and behaviors, which essentially combines data and function. Java models almost everything with objects. The conceptual consistency makes Java easy to understand for beginners, but it doesn't fit every problem well.

More universal than object, data and function are two concepts found in all programming languages. Functions are simulated with interfaces in Java. When you do need a function, you have to define a class which implements the interface. The following code snippet demonstrates the Java way of simulating a function of type T -> R with a generic interface.

interface F1<T, R> {
  R apply(T arg);
}

Every time you need a function, you have to either explicitly or anonymously define a class to implement the interface. It causes a bunch of syntactic noise around the core feature code which you really need to write. Every once in a while, we see complains about this in the community.

// Java 6
// option 1: named class
class AgePredicate implements F1<Employee, Boolean> {
  public Boolean apply(Employee employee) {
    return employee.getAge() > 35; // business logic
  }
}
employees.filter(new AgePredicate());

// option 2: anonymous class
employees.filter(new F1<Employee, Boolean>() {
  public Boolean apply(Employee employee) {
    return employee.getAge() > 35; // business logic
  }
});

With the advent of lambda expression feature in Java 8, life is much easier. Java 8 still uses functional interfaces to represent functions, but there's no need to define a class any more:

// Java 8
employees.filter(employee -> employee.getAge() > 35);

Lambda != Functional Programming

Programmers are lazy, they don't like writing boilerplate code, they love conciseness. However, some programmers may have the illusion that functional programming is all about lambda expressions. This is simply not correct, there're more stuff in functional programming than lambda expressions.

There're 2 things that shape functional programming:

1. Higher-order function: functions as the first class citizen;

2. Functional composition: the unique way of composing small functions into a larger one.

Lambda expressions can be considered as a syntactic sugar to create functions concisely, but it's not indispensable. The key is you really understand the nature of function and how functions work together.

This article just wanted to impress you that functional programming has always been there in Java since the introduction of Generics feature in version 5. Most of our programmers just overlooked it.

Let's get started with a simple question:

map is a famous higher-order function which maps a transform function f of type T -> R over a list of type [T] (alias of List<T>) and returns a list of type [R]. For example, map x -> x * x over [1, 2, 3] will yield [1, 4, 9].

In terms of API design, there can be different options, so the question is which one in the following forms is the best in general?

1. map(x -> x * x, [1, 2, 3])
2. map([1, 2, 3], x -> x * x)
3. [1, 2, 3].map(x -> x * x)

The first 2 forms are both in functional style, they only differ in parameter order. The third form is in OO style.

However, although they look similar, when it comes to API design, we should always prefer the first form, only choose other forms when you really have special reasons. If you don't understand the reason now, don't worry, I'll explain it later.

Currying

Currying is an extremely important feature of functional programming. Currying means breaking a function with many arguments into a series of functions that each takes one argument and ultimately produce the same result as the original function.

Only a few programming languages support Currying at the language level. Haskell and Scala fall into this category, see currying in Haskell and currying in Scala for details. Many other modern languages supporting lambda expression (such as C#, Python and JavaScript) don't support Currying natively.

Let's get a sense of Currying with a Haskell code. Say we define a function add as below:

-- Haskell

add :: Int -> Int -> Int
add x y = x + y

The type of add is Int -> Int -> Int meaning it's a function which takes 2 Int arguments and returns an Int value. I hope the audience can get used to the Haskell form of function signature. It's a better form than the Java counterpart int add(int, int).

The interesting thing is what would happen if we don't feed all the arguments at once to add? Let's do an experiment in GHCi:

// Haskell (GHCi)

> :t add
add :: Int -> Int -> Int

> :t add 2
add 2 :: Int -> Int

> :t add 2 3
add 2 3 :: Int

The result shows: 1) the type of add if Int -> Int -> Int; 2) the type of add 2 is Int -> Int; 3) the type of `add 2 3 is Int. This explains why we prefer the arrow form of function signature, because it's intuitive. Originally you have a type Int -> Int -> Int, after feeding one Int, you get Int -> Int, after feeding another Int, you get Int.

Be aware that similar things will not work in C#, JavaScript or Python. Let's take a look at JavaScript for example:

// JavaScript
function add(x, y) {
  return x + y;
}

add(2); // add(2) => add(2, undefined) => NaN

add(2) doesn't return a function as what we got in Haskell, instead it automatically uses undefined as the second argument. That means Currying is not a feature of the JavaScript language.

Usually, you will need to do something like this to get the curried version of add:

// JavaScript
function add() {
  return function(x) { return function(y) { x + y; } }
}

add; // function of type object -> object -> object
add(2); // function of type object -> object
add(2)(3); // value 5

Java is no better than JavaScript on this point, but we are able to come up with a workaround. In the following snippet, F2<T1, T2, R> stands for a curried function of type T1 -> T2 -> R:

// Java 6
/** Function of type T1 -> T2 -> R */
public abstract class F2<T1, T2, R> extends F1<T1, F1<T2, R>> {
  /** Subclasses override this method to implement the function */
  public abstract R apply(T1 arg1, T2 arg2);

  /** Partial application */
  public final F1<T2, R> apply(final T1 arg1) {
    return new F1<T2, R>() {
      @Override public R apply(T2 arg2) {
        return F2.this.apply(arg1, arg2);
      };
    };
  }
}

Just put definitions of F1<T, R>, F2<T1, T2, R> ... in a library, then we can define curried functions as follows:

// Java 6
class Strings { 
  /** Curried form of times(int, String) */
  public static F2<Integer, String, String> times() {
    return new F2<Integer, String, String>() {
      @Override String apply(Integer n, String str) {
        times(n, str);
      }
    };
  }

  public static String times(int n, String str) {
     ... // implementation
  }
}

Then we can use it as:

F2<Integer, String, String> nTimes = times();
F1<String, String> threeTimes = nTimes.apply(3);
threeTimes.apply("foo"); // "foofoofoo"

In Java 8, things get easier, you don't need to write the curried version manually. With the method reference feature, we can come up with a reusable function to convert a non-curried function into a curried one. :

// Java 8
F2<Integer, String, String> times = Currying.<Integer, String, String>curry(Strings::times);
assertEquals("abcabcabc", times.apply(3).apply("abc"));

More details here.

Functional Composition

All the things we did in the the previous section is to get the capability of partial application. Why partial application matters? Let's look at a problem:

Given a string of words separated by spaces, e.g. "I love programming in Java", write a function String convert(String input) to: 1) reverse the order of words; 2) convert the words to upper case; 3) join the words by underscore. For example, convert("I love programming in Java") will yield "JAVA_IN_PROGRAMMING_LOVE_I".

In Java 6, we can actually do like this:

// Java 6
String convert(String str) {
  // _ composes multiple functions into one function
  F1<String, String> f = _(split(" "), Lists.<String>reverse(), map(toUpperCase()), join("_"));
  return f.apply(str);
}

More details here.

The point here is the unique way of composing a bunch of small functions into a larger one.

Every programming language has its way to composition, they only differ in how. We call the style above functional composition. One of the biggest differences between functional composition and OO composition is that we don't even need to mention the data in functional composition, you can just partially apply the curried functions and compose then together. It's also called Point-Free style.

In functional composition, we need to pay special attention to the type of values and functions. For example, the type of compose function _ is (T -> U) -> (U -> R) -> (T -> R) meaning given a function f1 of type T -> U and a function f2 of type U -> R, it will return a function of type T -> R. So the restriction here is the return type of f1 is the parameter type of f2. If it's not satisfied, the compiler and IDE will warn you. Let's look at the example, since we want to have convert of type String -> String, the type of split(" ") must be String -> T where T can be anything, then since it's connected to Lists.<String>reverse(), here T is forced to be List<String>.

The following diagrams depicts the type of partially applied functions and composed functions:

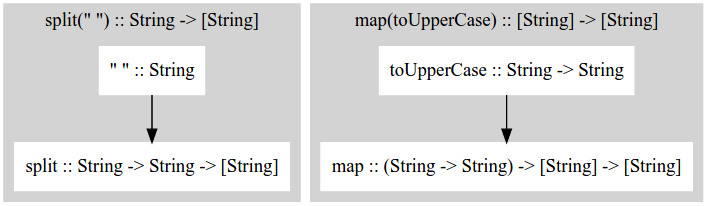
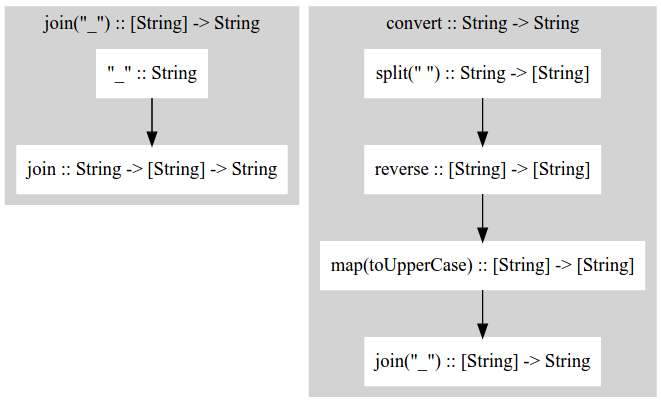
Functional composition also depends on the way you define the types. Recall the 3 forms of map:

1. map(x -> x * x, [1, 2, 3])
2. map([1, 2, 3], x -> x * x)
3. [1, 2, 3].map(x -> x * x)

In general, we always prefer the first form which puts data at the end of the parameter list. One important reason for this is easier to partially apply the function and compose it with other functions. I'm not saying the second form doesn't work, if you have an existing function say f :: D -> T -> R which puts data at the beginning, just use flip(f) to turn the type into T -> D -> R, the implementation will not be changed.

In the next section, I'll tell another important reason for preferring the first form.