Spectral Clustering

Spectral Clustering（谱聚类）是一种基于图论的聚类方法，它能够识别任意形状的样本空间且收敛于全局最有解，其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类，可见，它与样本feature无关而只与样本个数有关。

一、图的划分

图划分的目的是将有权无向图划分为两个或以上子图，使得子图规模差不多而割边权重之和最小。图的划分可以看做是有约束的最优化问题，它的目的是看怎么把每个点划分到某个子图中，比较不幸的是当你选择各种目标函数后发现该优化问题往往是NP-hard的。

怎么解决这个问题呢？松弛方法往往是一种利器（比如SVM中的松弛变量），对于图的划分可以认为能够将某个点的一部分划分在子图1中，另一部分划分在子图2中，而不是非此即彼，使用松弛方法的目的是将组合优化问题转化为数值优化问题，从而可以在多项式时间内解决之，最后在还原划分时可以通过阈值来还原，或者使用类似K-Means这样的方法，之后会有相关说明。

二、相关定义

1、用 ${G=(V,E)}$ 表示无向图，其中 ${V}$ 和 ${E}$ 分别为其顶点集和边集；

2、说某条边属于某个子图是指该边的两个顶点都包含在子图中；

3、假设边 ${e}$ 的两个不同端点为 ${i}$ 和 ${j}$ ，则该边的权重用 ${w_{i,j}}$ 表示，对于无向无环图有 ${w_{i,j}=w_{j,i}}$ 且 ${w_{i,i}=0}$ ，为方便以下的“图”都指无向无环图；

4、对于图的某种划分方案的 ${Cut}$ 定义为：所有两端点不在同一子图中的边的权重之和，它可以被看成该划分方案的损失函数，希望这种损失越小越好，本文以二分无向图为例，假设原无向图 ${G}$ 被划分为 ${G_1}$ 和 ${G_2}$ ，那么有：

${Cut(G_1,G_2)=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}$

三、Laplacian矩阵

假设无向图 ${G}$ 被划分为 ${G_1}$ 和 ${G_2}$ 两个子图，该图的顶点数为： ${n=|V|}$ ，用 ${q}$ 表示 ${n}$ 维指示向量，表明该划分方案，每个分量定义如下：

${q_i=\begin{} \begin{cases} c_1 \quad \quad \quad \quad \quad i \in G_1\\ c_2 \quad \quad \quad \quad \quad i \in G_2 \end{cases}}$

于是有：

${Cut(G_1,G_2)=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}=\frac{\sum\limit_{i=1}^n \sum\limit_{j=1}^n w_{i,j}(q_i-q_j)^2}{2(c_1-c_2)^2}}$

又因为：

${\sum\limit_{i=1}^n \sum\limit_{j=1}^n w_{i,j}(q_i-q_j)^2=\sum\limit_{i=1}^n \sum\limit_{j=1}^n w_{i,j}({q_i^2}-{2q_i q_j} +\ q_j^2})}$

${=\sum\limit_{i=1}^n\sum\limit_{j=1}^n -2w_{i,j} q_i q_j +\ \sum\limit_{i=1}^n \sum\limit_{j=1}^n w_{i,j}(q_i^2 +\ q_j^2)}$

${=\sum\limit_{i=1}^n\sum\limit_{j=1}^n -2w_{i,j} q_i q_j +\ \sum\limit_{i=1}^n 2 q_i^2 (\sum\limit_{j=1}^n w_{i,j})}$

${=2 q^T (D-W)q}$

其中， ${D}$ 为对角矩阵，对角线元素为：

${D_{i,i}=\sum\limit_{j=1}^n w_{i,j}}$

${W}$ 为权重矩阵：

${W_{i,j}=w_{i,j}}$ 且 ${W_{i,i}=0}$ 。

重新定义一个对称矩阵 ${L}$ ，它便是Laplacian矩阵：

${L=D-W}$

矩阵元素为：

${L_{i,j}=\begin{} \begin{cases} \sum\limit_{j=1}^n w_{i,j} \quad \quad \quad i=j\\-w_{i,j} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad i \neq j \end{cases}}$

进一步观察：

${q^T L q=\frac{1}{2}\sum\limit_{i=1}^n \sum\limit_{j=1}^n w_{i,j}(q_i-q_j)^2}$

如果所有权重值都为非负，那么就有 ${q^T L q \geq 0}$ ，这说明Laplacian矩阵 ${L}$ 是半正定矩阵；而当无向图为连通图时 ${L}$ 有特征值0且对应特征向量为 ${[1,1,1...1]^T}$ ，这反映了，如果将无向图 ${G}$ 划分成两个子图，一个为其本身，另一个为空时， ${Cut}$ 为0(当然，这种划分是没有意义的)。

其实上面推导的目的在于得到下面的关系：

${Cut(G_1,G_2)=\frac{q^T L q}{(c_1-c_2)^2}}$

这个等式的核心价值在于：将最小化划分 ${Cut}$ 的问题转变为最小化二次函数 ${q^T L q}$ ；从另一个角度看，实际上是把原来求离散值松弛为求连续实数值。

观察下图：

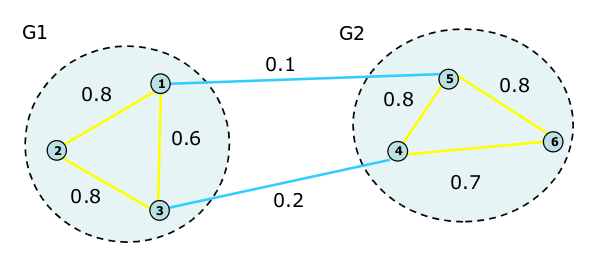
图1

它所对应的 ${W}$ 矩阵为：

       [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  0.0  0.8  0.6  0.0  0.1  0.0
[2,]  0.8  0.0  0.8  0.0  0.0  0.0
[3,]  0.6  0.8  0.0  0.2  0.0  0.0
[4,]  0.0  0.0  0.2  0.0  0.8  0.7
[5,]  0.1  0.0  0.0  0.8  0.0  0.8
[6,]  0.0  0.0  0.0  0.7  0.8  0.0

矩阵为：


       [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  1.5  0.0  0.0  0.0  0.0  0.0
[2,]  0.0  1.6  0.0  0.0  0.0  0.0
[3,]  0.0  0.0  1.6  0.0  0.0  0.0
[4,]  0.0  0.0  0.0  1.7  0.0  0.0
[5,]  0.0  0.0  0.0  0.0  1.7  0.0
[6,]  0.0  0.0  0.0  0.0  0.0  1.5
Laplacian矩阵为：

       [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  1.5 -0.8 -0.6  0.0 -0.1  0.0
[2,] -0.8  1.6 -0.8  0.0  0.0  0.0
[3,] -0.6 -0.8  1.6 -0.2  0.0  0.0
[4,]  0.0  0.0 -0.2  1.7 -0.8 -0.7
[5,] -0.1  0.0  0.0 -0.8  1.7 -0.8
[6,]  0.0  0.0  0.0 -0.7 -0.8  1.5

   Laplacian矩阵是一种有效表示图的方式，任何一个Laplacian矩阵都对应一个权重非负地无向有权图，而满足以下条件的就是Laplacian矩阵：
 1、为对称半正定矩阵，保证所有特征值都大于等于0；
2、矩阵有唯一的0特征值，其对应的特征向量为，它反映了图的一种划分方式：一个子图包含原图所有端点，另一个子图为空。

四、划分方法

1、Minimum Cut 方法

考虑最简单情况，另 ${C_1=1=-C2}$ ，无向图划分指示向量定义为:

${q_i=\begin{} \begin{cases} 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad i \in G_1\\ -1 \quad \quad \quad \quad \quad i \in G_2 \end{cases}}$

要优化的目标为 ${Cut(G_1,G_2)}$ ，由之前的推导可以将该问题松弛为以下问题：

$\begin{eqnarray*} & \min &q^TLq\\ & s.t.& [1,1,....1]^T q=0\quad \\ && q^Tq =n \quad \end{eqnarray*}$

从这个问题的形式可以联想到Rayleigh quotient：

${R(L,q)=\frac{q^TLq}{q^Tq}}$

原问题的最优解就是该Rayleigh quotient的最优解，而由Rayleigh quotient的性质可知：它的最小值，第二小值，......，最大值分别对应矩阵 ${L}$ 的最小特征值，第二小特征值，......，最大特征值，且极值 $q$ 在相应的特征向量处取得，即需要求解下特征系统的特征值和特征向量：

${Lq=\lambda q}$

这里需要注意约束条件 ${[1,1,....1]^Tq=0}$ ，显然 ${L}$ 的最小特征值为0,此时对应特征向量为 ${[1,1,....1]^T}$ ，不满足这个约束条件(剔除了无意义划分)，于是最优解应该在第二小特征值对应的特征向量处取得。

当然，求得特征向量后还要考虑如何恢复划分，比如可以这样：特征向量分量值为正所对应的端点划分为 ${G_1}$ ，反之划分为 ${G_2}$ ；也可以这样：将特征向量分量值从小到大排列，以中位数为界划分 ${G_1}$ 和 ${G_2}$ ；还可以用K-Means算法聚类。

2、Ratio Cut 方法

实际当中，划分图时除了要考虑最小化 ${Cut}$ 外还要考虑划分的平衡性，为缓解出现类似一个子图包含非常多端点而另一个只包含很少端点的情况，出现了Ratio Cut，它衡量子图大小的标准是子图包含的端点个数。

定义 ${n_1}$ 为子图1包含端点数， ${n_2}$ 为子图2包含端点数， ${n_2=n-n_1}$ ，则优化目标函数为：

${obj=Cut(G_1,G_2)*(\frac{1}{n_1}+\ \frac{1}{n_2})}$

其中：

${Cut(G_1,G_2)=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}$

做一个简单变换：

${obj=Cut(G_1,G_2)*(\frac{1}{n_1}+\ \frac{1}{n_2})=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}*(\frac{1}{n_1}+\ \frac{1}{n_2})}$

${=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}*(\frac{n_1+\ n_2}{n_1n_2})=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}*(\frac{(n_1+\ n_2)^2}{n_1n_2n})}$

${=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}*(\sqrt{\frac{n_1}{n_2 n}}+\ \sqrt{\frac{n_2}{n_1 n}})^2}$

${=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}*(q_i-q_j)^2}$

其中：

${q_i=\begin{} \begin{cases} \sqrt{\frac{n_1}{n_2 n}} \quad \quad \quad \quad \quad \quad \quad i \in G_1\\ -\sqrt{\frac{n_2}{n_1 n}} \quad \quad i \in G_2 \end{cases}}$

看吧，这形式多给力，原问题就松弛为下面这个问题了：

$\begin{eqnarray*} & \min &q^TLq\\ & s.t.& q^T e=0\quad \\ && q^Tq =1 \quad \end{eqnarray*}$

依然用Rayleigh quotient求解其第二小特征值及其特征向量。

3、Normalized Cut 方法

与Ratio Cut类似，不同之处是，它衡量子图大小的标准是：子图各个端点的Degree之和。

定义： ${d_1}$ 为子图1Degree之和：

${d_1=\sum\limit_{i \in G_1}d_i}$

${d_2}$ 为子图2Degree之和：

${d_2=\sum\limit_{i \in G_2}d_i}$

则优化目标函数为：

${obj=Cut(G_1,G_2)*(\frac{1}{d_1}+\ \frac{1}{d_2})=\sum\limit_{i \in G_1,j \in G_2}w_{i,j}}*(q_i-q_j)^2}$

其中：

${q_i=\begin{} \begin{cases} \sqrt{\frac{d_1}{d_2 d}} \quad \quad \quad \quad \quad \quad \quad i \in G_1\\ -\sqrt{\frac{d_2}{d_1 d}} \quad \quad i \in G_2 \end{cases}}$

原问题就松弛为下面这个问题了：

$\begin{eqnarray*} & \min &q^TLq\\ & s.t.& q^TD e=0\quad \\ && q^TDq =1 \quad \end{eqnarray*}$

用泛化的Rayleigh quotient表示为：

${R(L,q)=\frac{q^TLq}{q^TDq}}$

那问题就变成求解下特征系统的特征值和特征向量：

${Lq=\lambda Dq}$ ——式子1

${\Leftrightarrow \quad \quad Lq=\lambda D^{\frac{1}{2}}D^{\frac{1}{2}} q}$ (注： ${D^{\frac{1}{2}}}$ 是一个对角矩阵，且 ${D^{\frac{1}{2}}D^{\frac{1}{2}}=D}$ )

${\Leftrightarrow \quad \quad D^{-\frac{1}{2}}LD^{-\frac{1}{2}}D^{\frac{1}{2}}q=\lambda D^{\frac{1}{2}} q}$

${\Leftrightarrow \quad \quad L^' q^'=\lambda q^'}$ (其中： ${L^'=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}}$ ， ${q^'=D^{\frac{1}{2}}q}$ ) ——式子2

显然，式子1和式子2有相同的特征值，但是对应特征值的特征向量关系为： ${q^'=D^{\frac{1}{2}}q}$ ，因此我们可以先求式子2的特征值及其特征向量，然后为每个特征向量乘以 ${D^{-\frac{1}{2}}}$ 就得到式子1的特征向量。

哦，对了，矩阵 ${L^'=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}}$ 叫做Normalized Laplacian，因为它对角线元素值都为1。

五、Spectral Clustering

上边说了这么多，其实就是想将图的划分应用于聚类，而且这种聚类只需要样本的相似矩阵即可，把每个样本看成图中的一个顶点，样本之间的相似度看成由这两点组成的边的权重值，那么相似矩阵就是一幅有权无向图。

对照图的划分方法，有下列两类Spectral Clustering算法，他们的区别在于Laplacian矩阵是否是规范化的：

1、Unnormalized Spectral Clustering算法

算法输入：样本相似矩阵S和要聚类的类别数K。

● 根据矩阵S建立权重矩阵W、三角矩阵D；

● 建立Laplacian矩阵L；

● 求矩阵L的前K小个特征值及其对应的特征向量，注意最小的那个特征值一定是0且对应的特征向量为 ${[1,1,....1]^T}$ ；

● 以这K组特征向量组成新的矩阵，其行数为样本数，列数为K，这里就是做了降维操作，从N维降到K维，(实际上除去那个全为1的向量维度降为了K-1)；

● 使用K-Means算法进行聚类，得到K个Cluster。

2、Normalized Spectral Clustering算法

算法输入：样本相似矩阵S和要聚类的类别数K。

● 根据矩阵S建立权重矩阵W、三角矩阵D；

● 建立Laplacian矩阵L以及 ${L^'=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}}$ ；

● 求矩阵 ${L^'}$ 的前K小个特征值及其对应的特征向量，注意最小的那个特征值一定是0且对应的特征向量为 ${[1,1,....1]^T}$ ；

● 利用 ${q^'=D^{\frac{1}{2}}q}$ 求得矩阵L前K小个特征向量；

● 以这K组特征向量组成新的矩阵，其行数为样本数N，列数为K；

● 使用K-Means算法进行聚类，得到K个Cluster。

3、以图1为例，取K=2，使用Unnormalized Spectral Clustering算法，此时聚类的对象其实就是矩阵L的第二小特征向量(使用R模拟)：

● L矩阵为：
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  1.5 -0.8 -0.6  0.0 -0.1  0.0
[2,] -0.8  1.6 -0.8  0.0  0.0  0.0
[3,] -0.6 -0.8  1.6 -0.2  0.0  0.0
[4,]  0.0  0.0 -0.2  1.7 -0.8 -0.7
[5,] -0.1  0.0  0.0 -0.8  1.7 -0.8
[6,]  0.0  0.0  0.0 -0.7 -0.8  1.5
● q<-eigen(L) 求得L的特征值和特征向量分别为：
$values
[1] 2.573487e+00 2.469025e+00 2.285298e+00 2.084006e+00 1.881842e-01 1.776357e-15

$vectors
            [,1]          [,2]        [,3]        [,4]       [,5]       [,6]
[1,] -0.10598786 -0.3788245748 -0.30546656  0.64690880  0.4084006 -0.4082483
[2,] -0.21517718  0.7063206485  0.30450981 -0.01441501  0.4418249 -0.4082483
[3,]  0.36782805 -0.3884382495  0.04461661 -0.63818761  0.3713186 -0.4082483
[4,] -0.61170644 -0.0009962363 -0.45451793 -0.33863293 -0.3713338 -0.4082483
[5,]  0.65221488  0.3509689196 -0.30495543  0.16645901 -0.4050475 -0.4082483
[6,] -0.08717145 -0.2890305075  0.71581349  0.17786774 -0.4451628 -0.4082483
● q$vectors[,5] 取第二小特征向量：
[1]  0.4084006  0.4418249  0.3713186 -0.3713338 -0.4050475 -0.4451628
● kmeans(q$vectors[,5],2) 利用K-Means算法聚类：
K-means clustering with 2 clusters of sizes 3, 3

Cluster means:
        [,1]
1 -0.4071814
2  0.4071814

Clustering vector:
[1] 2 2 2 1 1 1

Within cluster sum of squares by cluster:
[1] 0.002732195 0.002487796
 (between_SS / total_SS =  99.5 %)从结果上可以看到顶点1、2、3被聚为一类，顶点4、5、6被聚为一类，与实际情况相符。

在Mahout中已经有相应实现，放在下次学习吧。

六、总结

1、图划分问题中的关键点在于选择合适的指示向量 ${q}$ 并将其进行松弛化处理，从而将最小化划分 ${Cut}$ 的问题转变为最小化二次函数 ${q^T L q}$ ，进而转化为求Rayleigh quotient极值的问题；

2、 Spectral Clustering的各个阶段为：

● 选择合适的相似性函数计算相似度矩阵；

●计算矩阵L的特征值及其特征向量，比如可以用Lanczos迭代算法；
●如何选择K，可以采用启发式方法，比如，发现第1到m的特征值都挺小的，到了m+1突然变成较大的数，那么就可以选择K=m；
● 使用K-Means算法聚类，当然它不是唯一选择；
● Normalized Spectral Clustering在让Cluster间相似度最小而Cluster内部相似度最大方面表现要更好，所以首选这类方法。

六、参考资料

1、Chris Ding.《A Tutorial on Spectral Clustering》、《Data Mining using Matrix and Graphs》

2、Jonathan Richard Shewchuk. 《Spectral and Isoperimetric Graph Partitioning》

3、Denis Hamad、Philippe Biela.《Introduction to spectral clustering》

4、Francis R. Bach、Michael I. Jordan.《Learning Spectral Clustering》

5、丕子.http://www.zhizhihu.com/html/y2010/1141.html

posted on 2012-02-10 10:57 Leo Zhang 阅读(25433) 评论(14) 编辑收藏举报

刷新页面返回顶部

Leo Zhang