算法设计和数据结构学习_3(《数据结构和问题求解》part2笔记)
前言:
本节是data structures and algorithm analysis in c++ (second edition)中第2大部分的随手笔记,主要内容有算法复杂度分析,标准模板库介绍,递归思想和算法,常见的排序算法及其分析,随机数产生器和随机算法等。
Chap6:
一个算法的复杂度与输入数据量的大小,算法本身,编译器优化性能,所运行机器硬件的性能,算法本身等因素相关。从这些方面来看,即使是已经确定的2个算法F和G,我们也不能说2个算法的运行时间永远满足F(N)<=G(N)或者F(N)>=G(N). 一是当N比较小时,两者的相差太小以至于感觉不出来,二是当N大到一定程度时,F(N)和G(N)中的主要项(当为多项式时,则为指数值最高的那项)才能体现出优势,否则就会引入不小的误差。第三当然就是编译器性能,CPU性能等额外因素了。
在实际使用过程中,O(N^3)的算法一般要求输入数据不要过千,而O(N~2)算法一般不要求输入数据过万。
常见的算法复杂度从简单到复杂的表格:
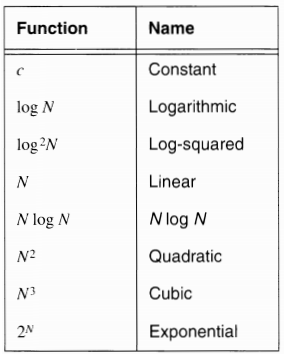
其中的算法复杂度表示所进行的数之间的加减乘除运算的次数。
即使一个算法A的最坏时间复杂度要比另外一个算法B的小,也不意味着A的平均复杂度比B的小,虽然大多数情况下确实是如此。
最大连续序列之和问题的复杂度可以为O(N),常见的是O(N^2),另外也可以是O(N^3)或者O(NlogN).
log(N)问题的引入常见的有:连续整数所需的位存储空间;双倍递增问题;半数递减问题。
搜索问题即查找问题,静态搜索算法指的是在搜索过程中不改变原始的数据。常见的静态搜索算法法有:序列搜索(在数据没有进行排序的情况下),二分搜索(已排序,只有当搜索范围较大时使用,当搜索范围较小时改为序列搜索会更好)。
检查算法的复杂度常见的有2种方法,第一是增加输入到N倍,看时间复杂度的输出,如果也是增加N倍,则可能是线性或者O(Nlog(N)),如果是增加N^2倍,则可能是O(N^2),如果是N^3倍,则有可能是O(N^3)。第二种方法是采用比值法,让实际算法的复杂度除以N,N^2,Nlog(N),N^3,并且同时增大N值,看比值的结果是收敛到0,还是趋于发散,或者趋于常数。如果是趋于常数,则被除数就是需要的时间复杂度表示了。
Chap7:
一般情况下数据结构都允许有插入操作,只不过有的数据结构可能只允许在特点的位置插入(比如队列,栈)。常见的数据结构操作还有删除,查找等。
栈中数据结构的insert,remove,find三种操作分别对应为push,pop和top。栈在编译器的设计中用得很多。栈的其它常见应用有符号匹配,数学运算等。
队列中的操作为enqueue,dequeue,getFront,分别为插入(后面),删除(前面),读取(前面)。
一个迭代器是指针原始类型,而不是类类型,因此它没有类成员函数,而是通过很多操作符重载来实现这些功能。
常见的容器有vector,list,maps,sets,一些容器允许有复制操作,但一些不允许,所有的容器必须提供empty(),begin(),end(),size(),getIterator()函数。其中getIterator()函数返回的iterator必须有hasNext(),next()函数,指向对应容器的指针和计数变量。
一般对容器的操作是返回一个引用,至于是常量引用还是普通引用需要看对应的容器是否为常量容器。所以一般的容器都有2种迭代器,const_iterator和iterator.
迭代器是容器和算法之间的桥梁,容器提供最大可能合理的iterator,而算法则需要最小可能合理的iterator。
在STL的sort中,默认的排序为从小到大。predicate为满足一些属性的functor,并且它的返回值为boolean,不能改变类中的数据。如果这个predicate只有单个参数的话,则它也叫做unary predicate.
find_if()算法返回一个迭代器,该迭代器指向第一个满足find_if()函数中的第3个参数,也即predicate。
Unary binder adapter是一个将双参数的function转换单参数的适配器。
C++对于pointer几乎都有新的解决方案,如reference取代pass by pointer、vector取代array、string取代char *、STL containter取代dynamic alloction。
vector的iterator是pointer,list的iterator就不是pointer,而是object利用operator overloading使它表面上的操作像pointer而已,但并不是一个pointer。
STL中常见的序列实现方法有基于数组的形式以及基于链表的形式。它们都有push_back,insert,pop_up等方法,这两种情况下各有优势。
STL中栈和队列的实现是通过序列容器(比如说vector,list,deque)调用适当的函数来实现的。
set是个序列容器,里面的元素不允许重复。但multiset中允许有重复的元素。
Map也是个有序的容器,里面的元素是以键值对的形式出现,一个key对应一个value,其中的key也是不能够重复的。multimap允许其中的key重复。map有常见的查找,删除,插入操作,其中查找删除都是针对一个pair进行的,而find只需传入key值即可(返回值依旧为pair)。map有个特有的操作:索引操作。
优先队列不一定是按照先后顺序来选取元素的,而是给队列中的每个object一个序列号,比如可以假设该序列号越小,表示对应的object越重要。因此优先队列(priority queues)每次只允许访问那些序列值最小的object,并且它需要有deleteMin和findMin方法。优先队列中是允许有重复元素的,因此它不能用set来实现,但可以用multiset来实现,不过由于multiset中实现了非常多的优先队列不需要的操作,这样的实现会很浪费资源。实际上优先队列的实现时采用二进制堆(binary heap)的形式。
STL中的算法部分有头文件<algorithm>,<numeric>和<funtional>组成。其中<algorithm>头文件比较大,实现了很多常见的算法,比如比较,交换,查找,遍历,排序等。<numeric>体积很小,只包括几个在序列上进行监督数学运算的模板函数,加法和乘法等。<functional>中定义了一些模板,用来声明函数对象的,比如常见的bind。
容器分类:
sequence containers: vector, deque, list, forward list, array;
Associative: set,multiset, map, multimap;
Unordered containers: unordered set/multiset/map/multimap;
其中的associative因为是ordered,所以没有push_back,pop_up等操作。Unordered containers常和hash函数连用。
vector内部的数据地址是连续的。
set/multiset, map/multimap是不允许对其中的元素进行赋值的。
常见的容器适配器有:stack, queue, priority queue.
Array based containers的指针(包括原始的指针,迭代器,引用等)有时候会失效,因为如果插入了数据后这些指针就有可能随机的乱指。
输入输出的iterator可以向前,不能向后。
常见的迭代器分类:Insert iterator包括(back_insert_iterator, front_insert_iterator),stream iterator, reverse iterator, more iterator(C++ 11).
模板中的那个变量的意义不仅限于表示不同的数据类型,也可以表示不同的数值,如果它表示的是不同的数值的时候,在使用模板时是需要给一个实际的数代替的,连用变量代替都不行。
在类中如果实现一个functor(即把类对象当函数用),则返回值类型应该放在关键字operator前,和操作符重载情况一样,例如:void operator()(string str){};在类中如果实现一个类型转换,则应该把关键字operator放在最前面,比如:operator string()const {return “X”};
在STL中常见的functor有:less, greater, greater_equal, less_equal, not_equal_to, logical_and, logical_not, logical_or, multiplies, minus, plus, divide, modulus, negate等。
模板中的参数需要在编译时间段内确定。
参数绑定机制(parameter binding):
假设我们需要将一个集合中的元素乘以10保存到一个vector中:
该集合为:set<int>myset = {1,2,3,4,5};
vector为:vector<int> vec;
我们可以采用函数模板:
OutputIterator transform (InputIterator first1, InputIterator last1,OutputIterator result, UnaryOperation op);
来实现,其中前2个参数分别为源数据来源的首末迭代器,参数3为目的地址迭代器,op为一元操作函数。我们要实现上面的功能,是可以采用funtor中的multiplies的,它的用法如下:int x = multiplies<int>(2,3),但问题是它需要2个参数,而tranform最后一个op只能接收一个参数,所以这里就需要采用parameter blinding机制了,将2个参数的函数转换成一个参数的函数,使用的是模板bind。用法如下:
bind (Fn&& fn, Args&&... args);
其中的fn为函数,args为参数或者placeholder编号,返回值也为一个函数,其参数个数示具体情况而定。
最后上面的集合乘以一个数的解决方法为(back_inserter为一个插入迭代器):
transform(myset.begin(), myset.end(), back_inserter(vec), bind(multiplies<int>(), placeholders::_1, 10));
bind(multiplies<int>(), placeholders::_1, 10)返回的是单参数的函数。当然bind函数是在c++ 11中才有的,在老版本(比如C++ 03)中只有简单的bind1st, bind2nd. 另外这些bind函数是模板函数,如果我们需要将普通的函数转换成模板函数,则可以使用function模板(C++ 11, C++ 03为ptr_fun)。
eg:
double Pow(double x, double y) {
return pow(x, y);
}
auto f = function<double (double, double)>(Pow);
Chap8:
递归不是循环逻辑,所以我们在设计递归算法时要避免陷入循环逻辑,因为这等于死循环。
有些函数用递归表示比用具体的数学公式表达更好。
递归的4个准则:1. 必须至少有一个base case,这个base case不需要使用递归解决。2. 所有的递归都需要朝着base case的方向进行的。3. 我们总是认为递归中的调用会正常工作,所以遇到递归程序时我们不需要一步一步迭代进去理解,因为这样理解会很冗长,且容易出错,我们只需要用数学归纳法来验证一次就ok,其它的事情就交给计算机来做。4. 合成效应法则,决不在递归过程中重复调用同一接口。
递归的缺点是需要消耗比较大的内存(因为递归过程中前面的状态都需保存下来),但是某些问题比较适合用递归方法求解,且用递归方法求解的时间只比非递归的算法时间稍多,好处是递归处理时的代码更紧凑。
以十进制方式一个个输出数字A的每一部分,从高位开始,这个问题可以用递归方法来解决,每次都输出除掉个位数字后的数字,当只剩下一位时,就直接输出。
Driver routine在递归中用得很多,driver routine指的是第一次调用递归前测试某些变量的合理性,因为这些变量在递归过程中不再改变,测试一次就够了,测试完后就可以直接调用递归函数了。
递归算法虽然有效,但是也不能滥用,因为它的开销不小,所以在能够用简单循环完成的工作坚决不用递归实现。
递归的3个应用例子:1. N的阶乘;2. 二分搜索;3. 绘制一个刻度尺子;
如果两个数对N的模相等,则称它们对N为模一致,简写为A≡B(mod N),也就是同余。
模指数(modular exponentiation)是指计算X^N(mod P).
cup进行运算时,一般情况下多个小数相乘比少数个大数相乘用的时间要多些。
扩展的欧几里得算法:
对于不全为0的正整数a和b,gcd(a, b)表示a和b的最大公约数,则必然存在整数对
x和y,使得gcd(a, b) = ax + by,其中的x和y是整数,当然可以为负数。
乘法逆元问题:
求满足AX≡1(mod N)的X,其中的A和N是已知的,X为A的乘法逆元。这等价于求:AX+NY=1,这个可以结合扩展欧几里得算法以及迭代思想解决。
RSA算法的简单过程,假设Alice想发送加密的信息给bob:
首先Bob选择两个大的素数(100位以上)p和q,然后计算N=pq, N’=(p-1)(q-1),最后找到一个数e使得它和N’互质(有可能有多个e满足条件),接着计算e的乘法逆元d,最后Bob通知Alice两个数N和e,自己保留p,q,d。
假设Alice打算发送数字M,则她实际发送的数字为R=M.^e(mod N), 而Bolb收到数字后解码过程为:R.^d(mod N).
RSA算法的计算加密速度较慢,它是公共密钥加密方法,而一般的私钥加密速度更快,比如说DES算法,因此可以结合DES和RSA,即用DES加密需要传送的明文,然后用RSA加密DES算法的私钥一起传送,解密端首先解密出DES的私钥,然后解密密文。
分而治之是一个高效的递归算法,它包含两个部分:1.分,即每个小问题都可以用递归算法求得。2.合,原问题的求解可以由一些小问题的解构成,子问题之间是不能重合的。但分而治之的思想用于每次分成折半的小问题且附加线性的时间消耗时,其算法的时间复杂度为O(Nlog(N)).
Change-making问题为兑换最小零钱数问题,可以用动态规划算法求解(动态规划一般和贪婪思想,递归思想相关联)。
动态规划是把原问题分为相对简单的子问题,每个子问题的求解只算一次,然后存储,通过子问题的合并得到原问题的解,所以动态规划特别适用于有重叠的子问题。
3个经典思想中用到了递归:分而治之,动态规划,回溯法。
Chap9:
很多计算机程序直接或者间接的用到排序算法,并且排序算法很大程度上决定了程序运行算法的时间。
所有交换相邻元素的排序算法所需的平均时间复杂度为O(N^2).
证明一个算法复杂度的下限比证明它的上限要复杂不少,因为算法复杂度的下限 个比较抽象的概念。
Shell排序中,每个组内部是采用的插入排序。Shell排序中步长的选择是希尔排序的重要部分。只要最终步长为1任何步长串行都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为插入排序,这就保证了数据一定会被排序,shell算法也叫做消除间隙(gap)算法,其初始步长一般选择所需排序数组步长的一半,然后逐步一半一半递减(用得比较多的是除以2.2)。
Shell排序有一个特点就是H(k)-sort后进行的H(k-1)-sort不会改变H(k)-sort的排序结果。
快速排序算法是实际使用过程中速度最快的算法,它采用了递归的思想,平均时间复杂度为O(Nlog(N)),最坏情况为O(N^2),不过在统计上出现这种最坏情况的概率很小。快速排序算法的性能和选取的pivot(中心点)点有关,实际使用过程中不要每次都选第一个或者最后一个数作为pivot,较为合理的选择为中间的那个元素或者采用median-of-three方法,即选取3个数中第二大小的那个数。
在使用快速排序的分组过程中,如果碰到了数字和pivot相等是情况,则应该停止这次的扫描。在递归过程中,当剩下的元素个数比较小(比如说少于10)时则使用插入排序效果更好。
在一个数组中选择第k个大小的数,可以先排序,然后选择,但是这样代价会比较高,因为我们不需要像排序那样给出那么多的信息。将快速排序算法稍做更改就可以得到快速选择算法,其时间复杂度为O(N).
任何一个基于比较的排序算法的时间复杂度下限为O(log(N!)),约为Nlog(N),1.44N.
间接排序(indirect sorting)是为了减小使用模板时带来的copy开销,它引入了指针数组,排序移动只是针对指针,而不用复制数据。
由本章可以看出,插入排序比较适合数据量小的时候,shell排序适合数据量适中,快速排序是应用最广的,但是它的代码技巧比较多。
Chap10:
随机数产生器在现代密码学,仿真系统,搜索和排序算法,程序测试。
很多分布都可以从均一分布扩展而来,因此均一分布很一个非常重要的分布。
均一分布的数字需要满足一些重要的统计特性:连续的2个数的和为偶数或者奇数的概率相等;允许某些元素重复出现。线性同余产生器常用来产生均一分布。X’=AX%M; A=48271,M=2^31为时是常见的组合,因为它可以满足大部分的应用场合。
泊松分布是离散分布,适合于描述单位时间内随机事件发生的次数的概率分布,泊松分布可以从均一分布产生,假设需要产生均值为m的泊松分布,则连续产生(0,1)的数使其乘积取log后小于等于负m,则满足该条件的均一分布的个数就可以作为泊松分布的一个样本。
产生N个不同数字的随机序列,可以先产生N个有序序列,然后每次都将其中的一个数据和它前面的数据随机交换。
随机算法的最坏情况下的时间复杂度和确定性算法的最坏情况是一样的,可以将随机算法和排序算法结合,比如在快速排序中,pivot的选择可以采用随机算法,这样可以避免某些人为出现的bad input的情况。
试除法实现素数N测试:从3开始到sqrt(N)之间的所有奇数都不能被N整除,则N为素数。
运用费马小定理可以成功得到判断一个数是否为质数的一个方法:
如果对于任意满足1<b<p的b下式都成立:
b(p-1)≡1(mod p)
则p必定是一个质数。
这个定理告诉我们,判定一个数是否为质数,没有必要测试所有的小于p的自然数,只要测试所有的小于p的质数就可以了,事实上,测试小于p的平方根的所有质数就可以了。
c++中解决随机数问题时一般包含下面2个头文件:
#include <cstdlib>
#include <ctime>
然后随机数产生器的seed语句为:srand(time(0)),随机数产生器的语句为rand().
参考资料:
data structures and algorithm analysis in c++ (second edition),mark allen Weiss.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号