DSP复习笔记<7><chapter 5>
开坑时间记录 2023-06-11 17:28:35 希望我不会死在第五章😭 东西是真tnnd多啊,第四章都给我整出来心理阴影了啊啊啊不能骂人不能骂人
第五章 有限长离散变换
care points: DFT:定义、性质、对称关系、圆周卷积 FFT:基2,蝶形变换
注:虽然说是第五章,但会带过十一十二章的部分内容,而且它自己本身有14节比其它任意一章都多接近两倍,6
目的:较长的时域信号被分割为一组较短的序列,然后较短的序列进行有限长变换进入变换域,在变换域中处理之后由逆变换得到新的时域序列,然后将这些短序列通过适当的组合得到最终长序列。
5.1 正交变换
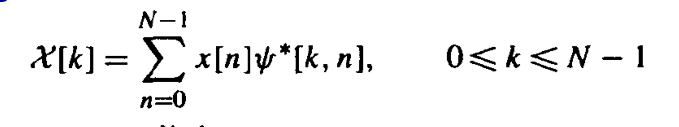 分析式,将x[n]分解为基序列的加权和
分析式,将x[n]分解为基序列的加权和
![]() 综合式,将基序列合并为原x[n]
综合式,将基序列合并为原x[n]
![]() 这是基序列
这是基序列
基序列满足如图条件为正交序列: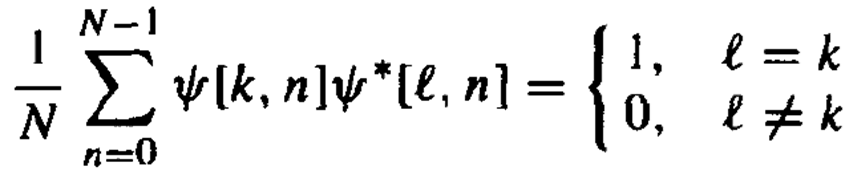
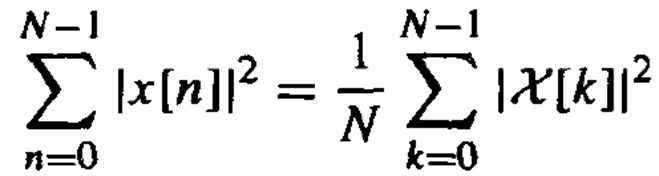 这是帕塞瓦尔定理
这是帕塞瓦尔定理
5.2 离散傅里叶变换 DFT
本章主要讨论离散傅里叶变换
前瞻:
连续时间傅里叶级数:![]()
连续时间傅里叶变换: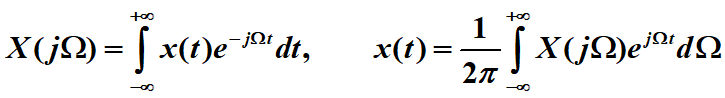
离散时间傅里叶变换:![]()
![]()
离散时间傅里叶级数:因为连续级数这样表示:![]()
离散等于采样: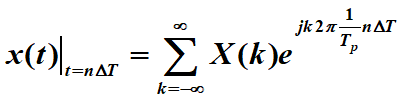 deta T是采样间隔,omega0是x(t)的角频率
deta T是采样间隔,omega0是x(t)的角频率![]() ,Tp是x(t)周期,又
,Tp是x(t)周期,又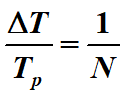
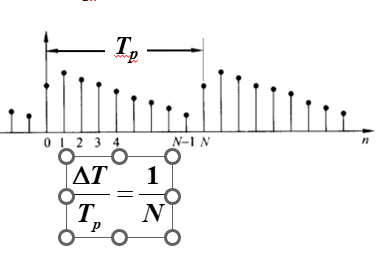
这个图可以看得很清楚,N是离散后序列的周期,
所以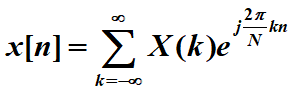 ,
,
对比5.1,可得基本序列是![]() ,其中
,其中![]()
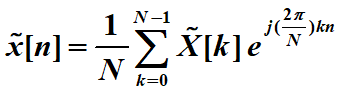
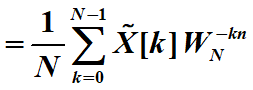 (令
(令![]() ,没记错的话这玩意叫旋转因子)
,没记错的话这玩意叫旋转因子)
得到DFS为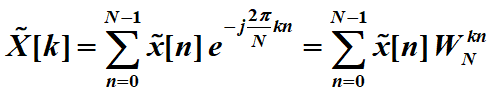
验证一下基序列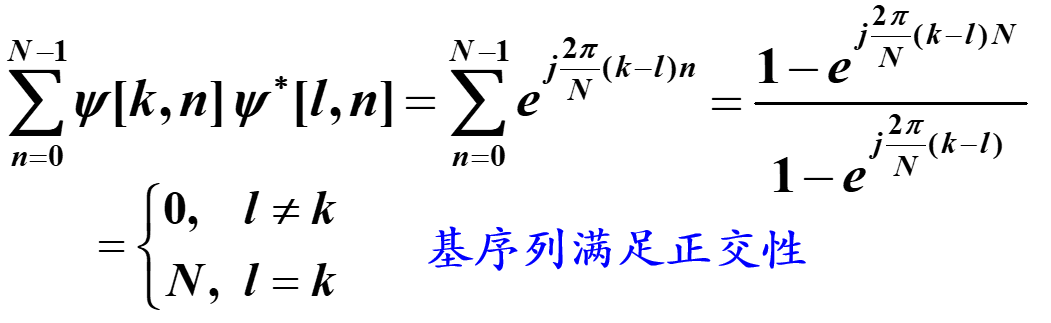 而且周期为N
而且周期为N
我也想知道是不是把DFS和DTFS混为一谈了
2.1 定义
时域中N点序列x[n]的离散傅里叶变换为
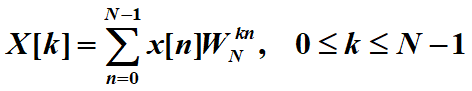
可以看出来DFT为一个长度为N的序列,如果k不限制范围的话,那就是周期为N的序列(上面提过了)
N点DFT:指的是DFT长度为N
建议看到这里先看一下5.3.1
逆变换IDFT则为:
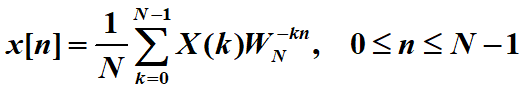
关于![]()
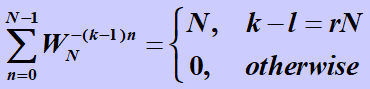 自证(为啥其他情况会等于0呢)
自证(为啥其他情况会等于0呢)
例题:
![]()
根据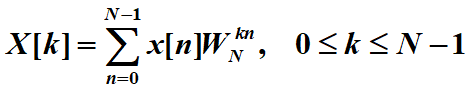
得到
![]()
![]()
![]()
![]()
2.2 计算复杂度问题
计算DFT和IDFT需要N2次复数相乘和N(N-1)次复数相加
为了减少运算复杂度,提出FFT算法,将计算量可减少至N(log2N)次运算
2.3 矩阵关系
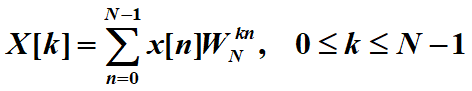
这个可以表示为![]()
其中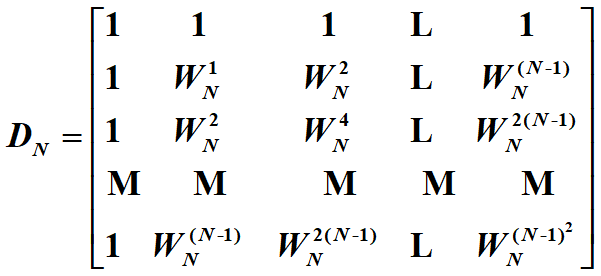
![]()
但我感觉我真考试的话应该不会用矩阵算
2.4 用matlab计算DFT
略
5.3 DTFT与DFT及其逆之间的关系
3.1 与离散时间傅里叶变换的关系
长度为N的序列x[n]的傅里叶变换为
![]()
![]()
它是以2π为周期的,我们在2π上进行w=2πk/N的等间隔抽样
会发现得到了它的N点DFT,所以DFT是信号DTFT的频率采样
![]()
3.2 用DFT对DTFT进行数值计算
看不懂,挖坑
3.3 通过插值由DFT得到DTFT
3.4 对傅里叶变换抽样
5.4 圆周卷积
考虑两个长度N的序列
他们的线性卷积:
![]()
圆周卷积:
![]()
满足交换律和结合律
例如:
求四点圆周卷积
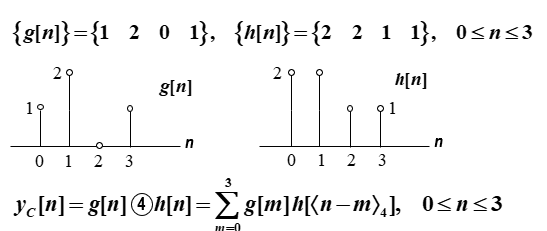
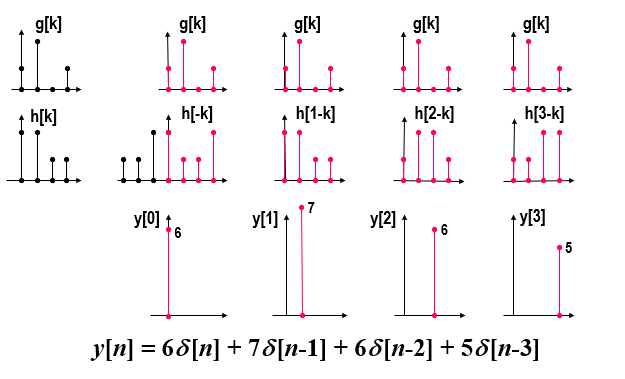
圆周和线性卷积
假设两个序列长度分别为N、M,则需要进行补零操作补到L
![]()
![]()
然后进行L点圆周运算
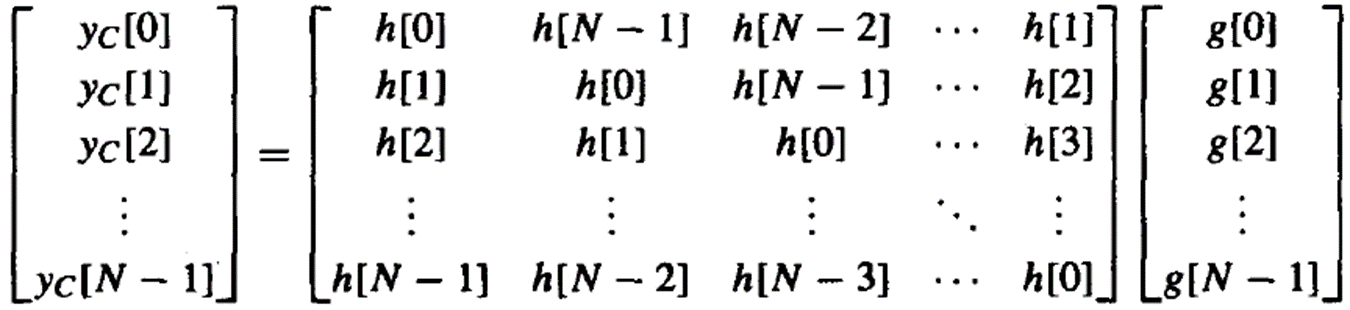
还有列表法
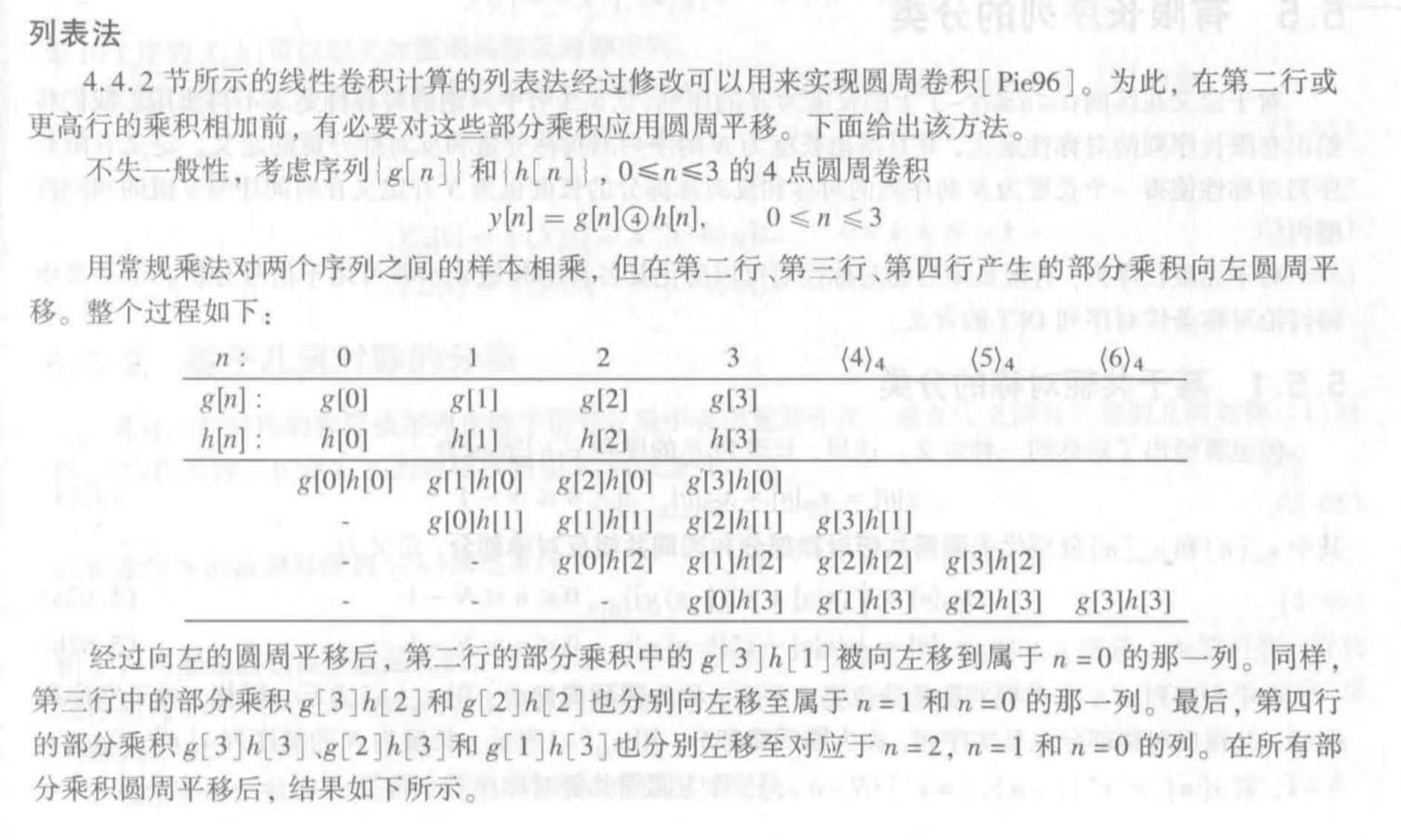
这是线性表

这是圆周表
5.5 有限长序列的分类
5.1 基于共轭对称的分类
有限长序列定义在0~N-1按理来说没法对称
但是可以搞圆周对称
序列表示为:
![]()
其中共轭对称:
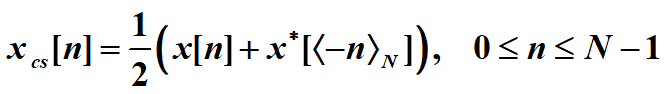
圆周共轭对称定义为:![]()
共轭反对称:
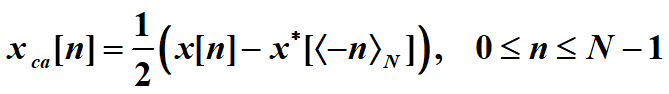
圆周共轭反对称定义为:
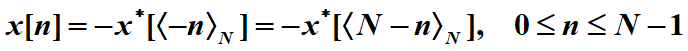
对于实序列
共轭对称部分为实序列xev[n]称为圆周偶部分
共轭反对称部分也为实序列xod[n]称为圆周奇部分
同样适用于频域、
5.2 基于几何对称的分类
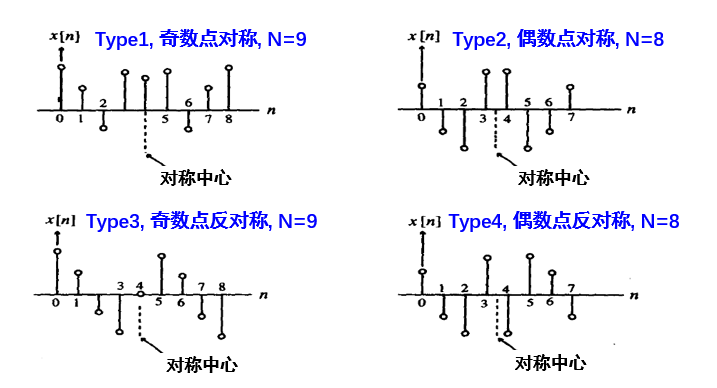
1.奇数个点
左列上:![]() 符合对称
符合对称
左列下:![]() 反对称
反对称
右列同理
5.6 DFT对称关系
1.复序列
a.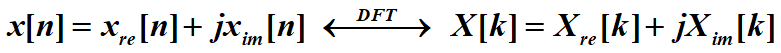
复序列可表示为实部加虚部
它的DFT变换为实部的DFT加虚部DFT(线性,无可厚非)
又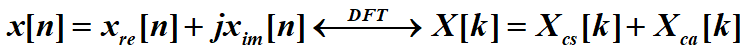
所以![]()
![]() (只从该式可看出)
(只从该式可看出)
b.如果加上![]()
则实部的DFT可写为![]()
即原信号实的实部DFT对应为原信号DFT的共轭对称
(见下方c推导)
c.DFT的复共轭可表示为
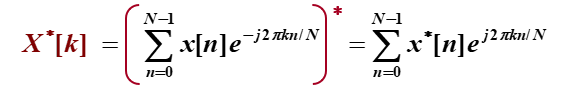
(同时可推导出![]() )
)
所以
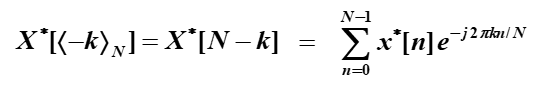
右边是xn共轭的DFT
即![]()
d. 另外![]()
![]()
即DFT可用原序列的共轭对称和共轭反对称表示
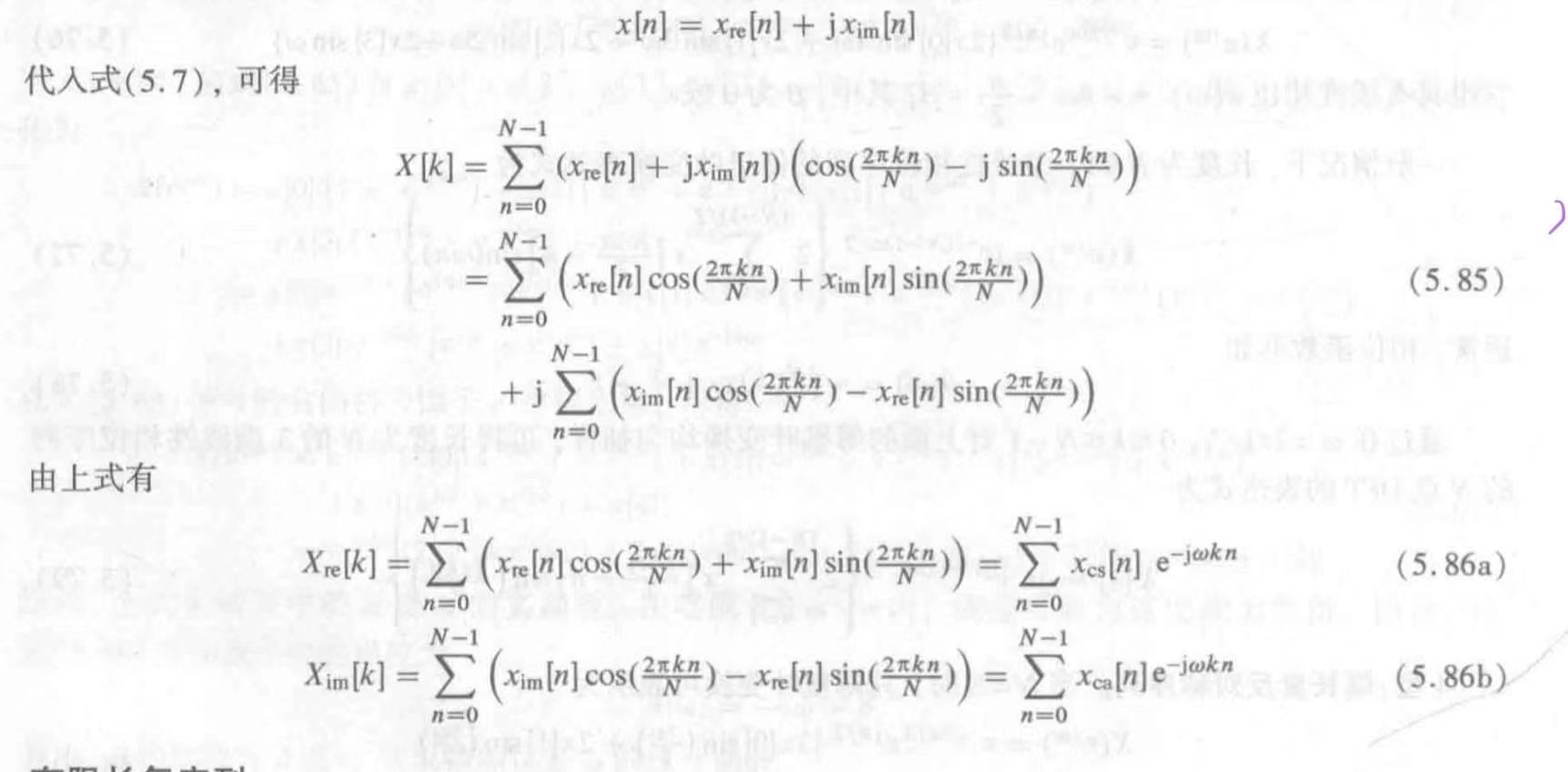
可证

这表里的上面都讲了,有点绕
2.实序列
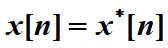
所以
![]()
![]()
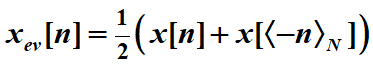 偶部分DFT为原信号DFT实部分
偶部分DFT为原信号DFT实部分
奇部分DFT为j乘虚部

5.7 离散傅里叶变换定理

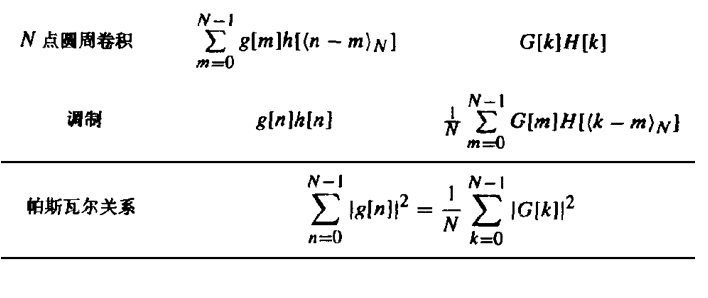
看表即可
其中N点圆周卷积的证明:
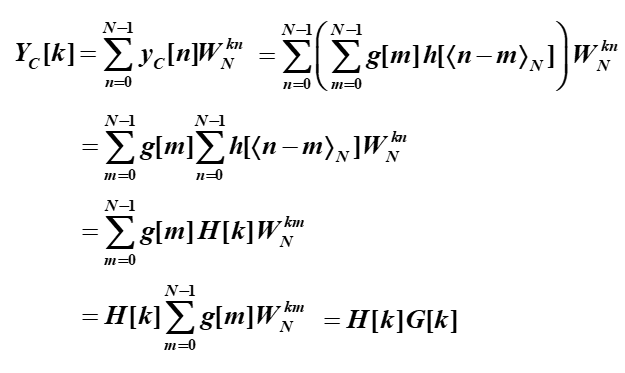
5.8 傅里叶域滤波
不作过多了解
5.9 计算实序列的DFT
好了,开始用较长篇幅讲一下第十一章的FFT
这是因为人类的节约引起的一个话题
因为,做圆周卷积用DFT相乘简化,但是DFT本身也需要简化
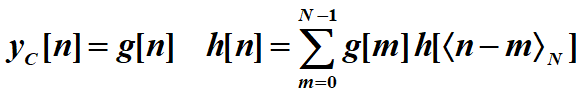 没看错应该是n*N次乘法
没看错应该是n*N次乘法
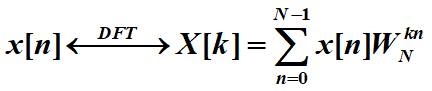
 额,我也看不出来是怎么统计的
额,我也看不出来是怎么统计的
所以需要FFT(快速傅里叶变换)
思想:将N点DFT分解为尺寸较小DFT
综合说一下旋转因子的性质
![]()
![]()
![]()
所以![]() 以N为周期
以N为周期
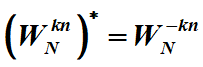 因为是纯复数
因为是纯复数
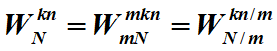
基2时间抽取FFT(要求原信号长度为2的M次方)
![]() (注意时域中序列长度为N)
(注意时域中序列长度为N)
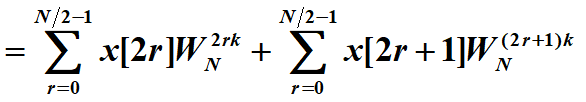 (右边是0,2,4,N-2,左边是1,3,5,N-1,总共还是N个)
(右边是0,2,4,N-2,左边是1,3,5,N-1,总共还是N个)
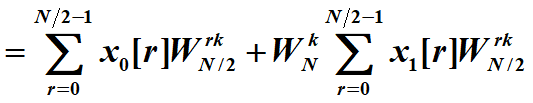 (为了凑DFT正好又与变量r无关所以左边把那个量拎出来了)
(为了凑DFT正好又与变量r无关所以左边把那个量拎出来了)
![]()
所以我看不懂这步
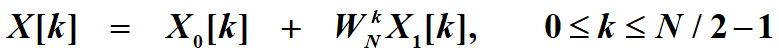
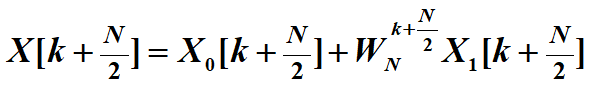
![]() (用来求后半部分的DFT但X0为啥不变啊)(哦,因为下标是N/2,相当于加了个周期,确实不变)
(用来求后半部分的DFT但X0为啥不变啊)(哦,因为下标是N/2,相当于加了个周期,确实不变)
整个蝶形图:
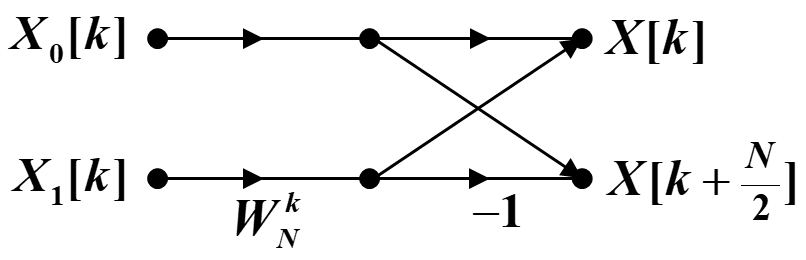
该蝶形图里用了一次复数乘和两次复数加
例:原信号长度为8 按时间抽取
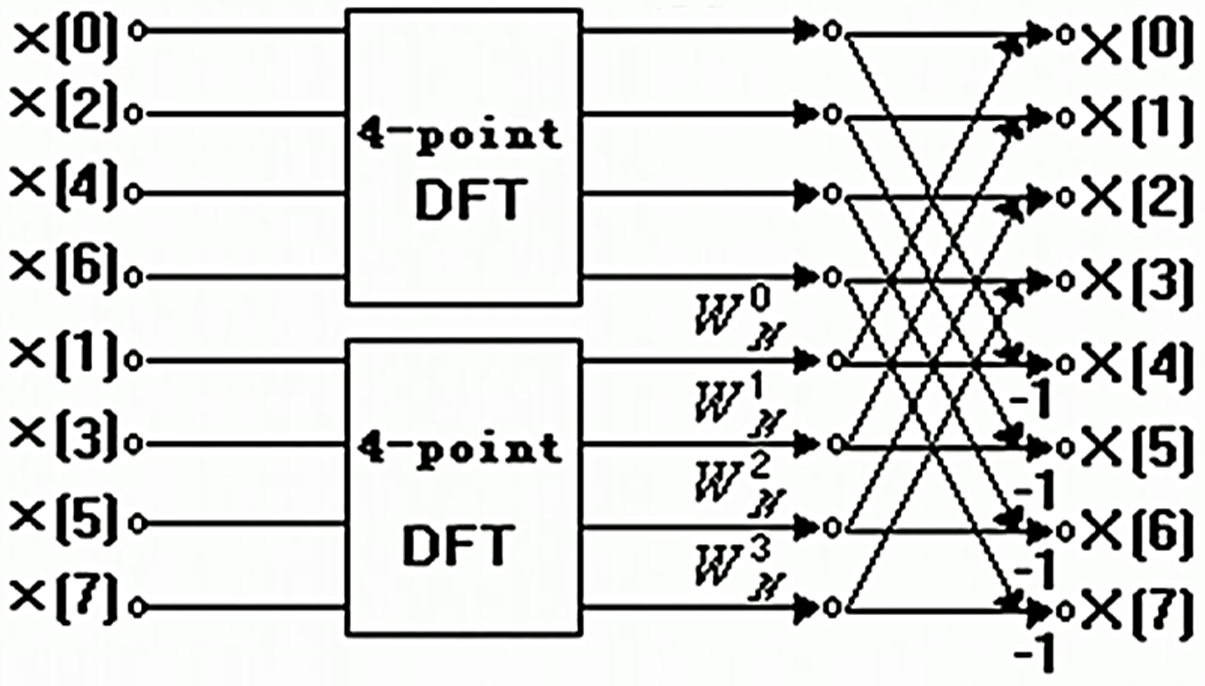
仔细看的话,X[0]等于x[0]
啊?
额,我反应过来了,比如X[4]对应的是后半段的第0位,所以对应奇偶序列中的第0位,即x[0]和x[1],而且由于是后半段,所以Wnk要乘负一,前半段同理,但是是不用乘负一的,直接加
然后我们把它变成真正意义上的基2,因为上面仍然做的4点DFT啊,还不够简单
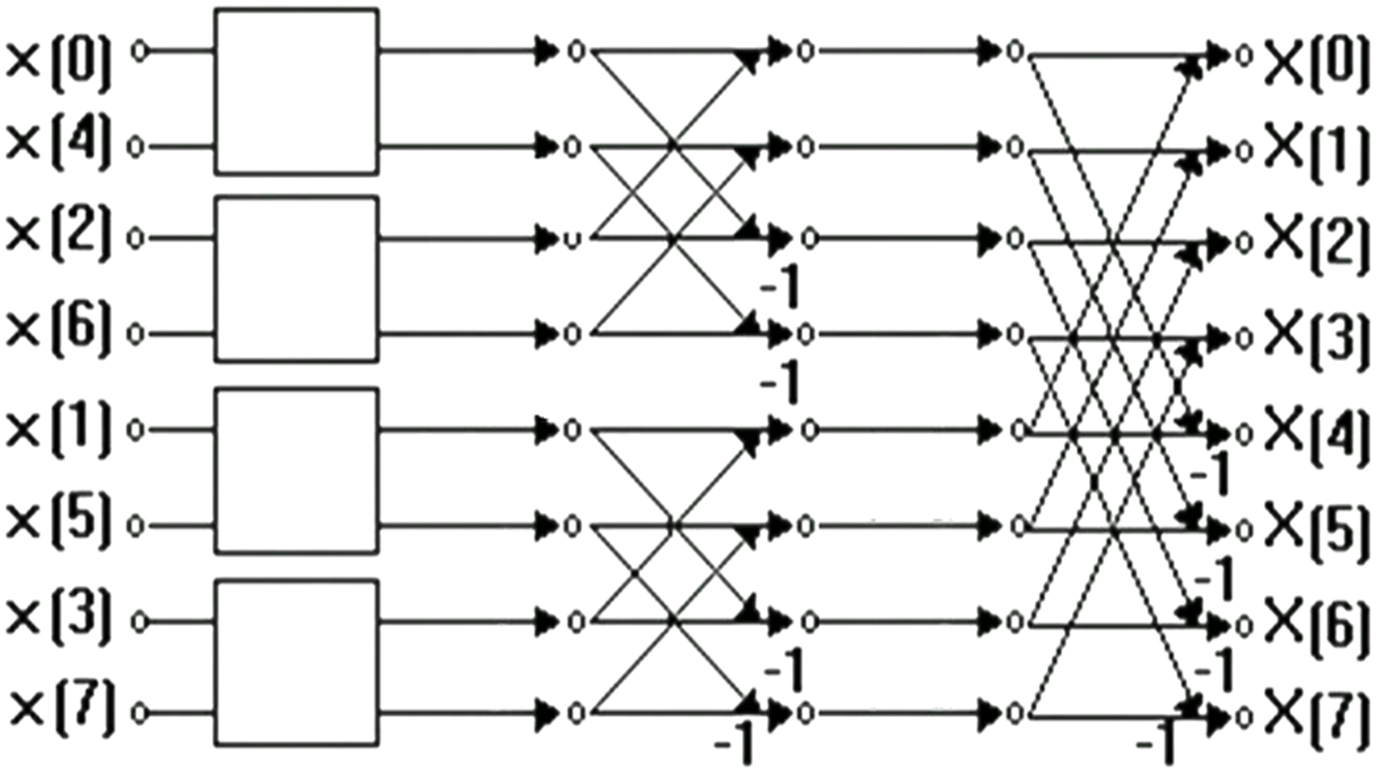
就是偶序列里再分奇偶,可以看到,例如,单独考虑本来的偶序列0,2,4,6
则0,4变成了偶序列(正常认知是奇,但是这样划分我也没办法,从0开始嘛)
2,6变成了基序列,做两点DFT变换,然后后面比如X[2],对应后半段的第1位,所以是由x[4]和x[6]求解
忽略上述错误推导
还是得慢慢推
比如X[2],对应前半段的第三位,所以是偶序列X[4]和奇序列X[5]的结合
没错,然后偶序列的X[4]是后半段的第一位(从0开始算),对应其偶序列的
完了,我又绕进去了,自己抄题对着写吧,
像这样
推导如下:
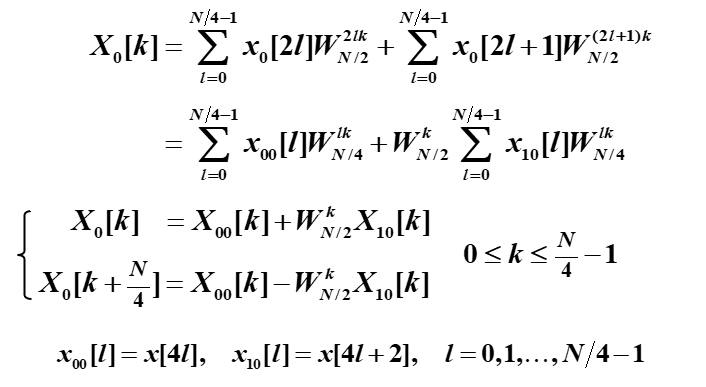
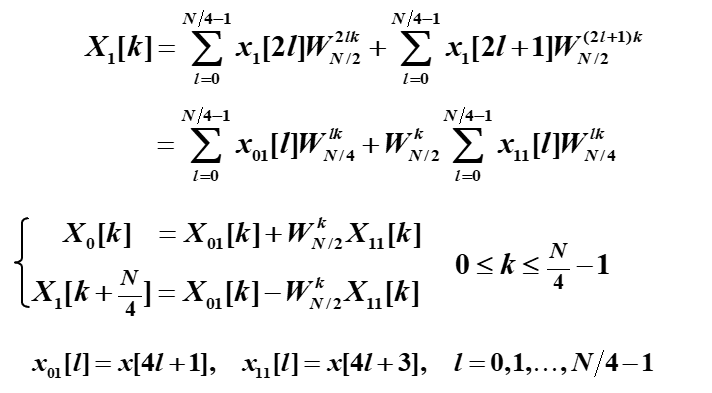
两点DFT:
![]()
所以把两点DFT再添进去完整蝶形图就是这样的
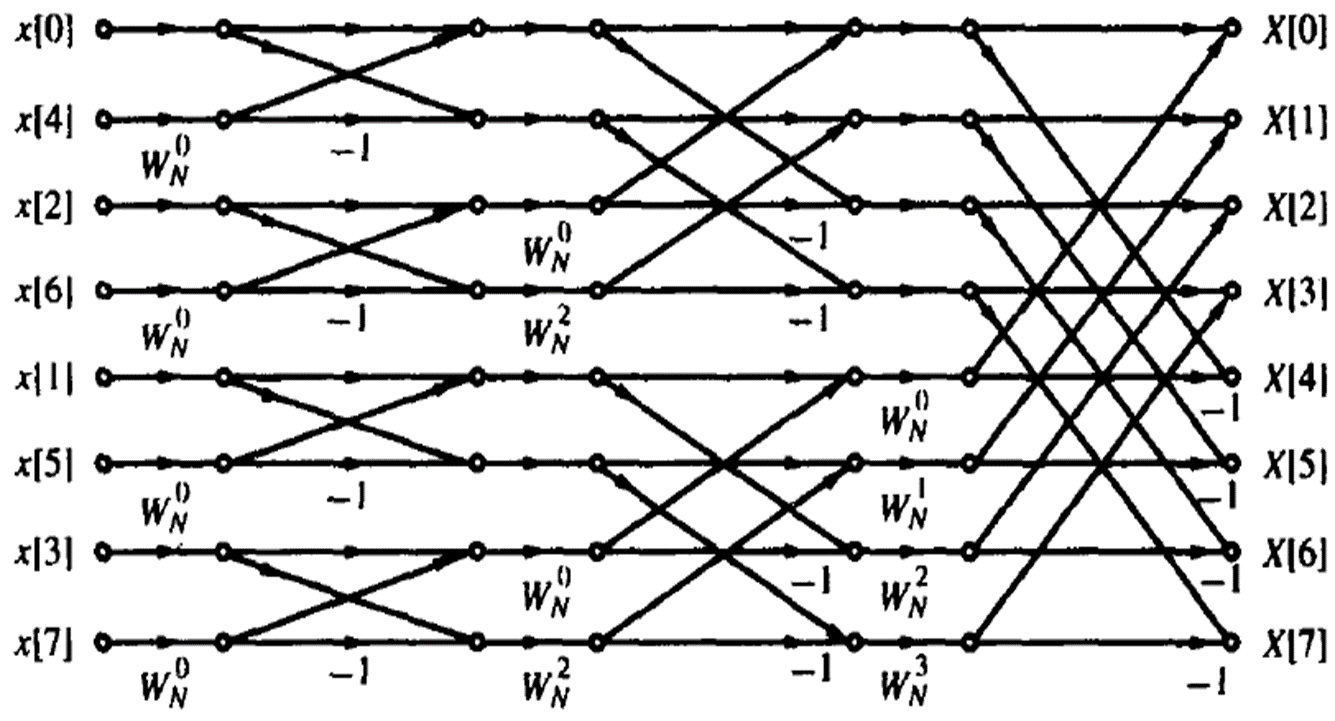
恕我直言,中间那段看不懂,头尾都能看懂,服了
计算复杂度应该不考吧(心虚)
基2频率抽取FFT
不太懂
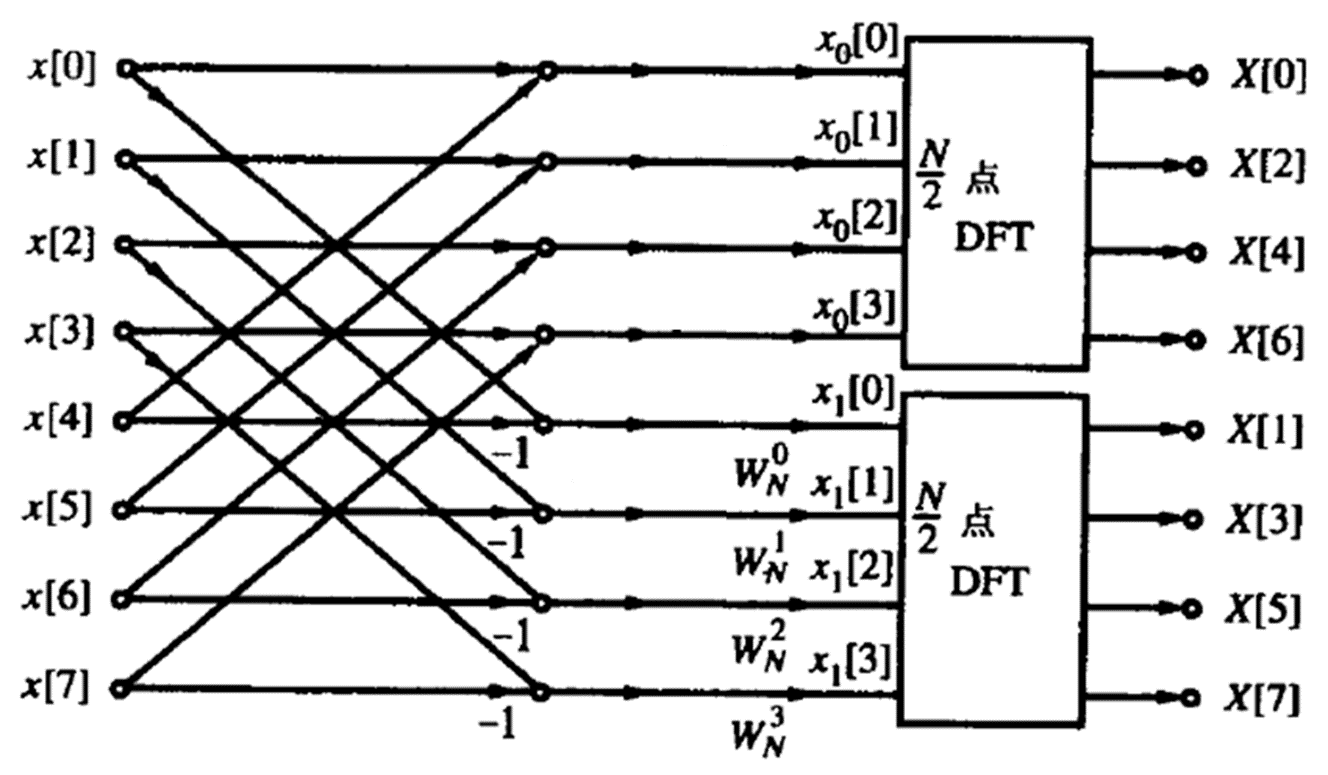
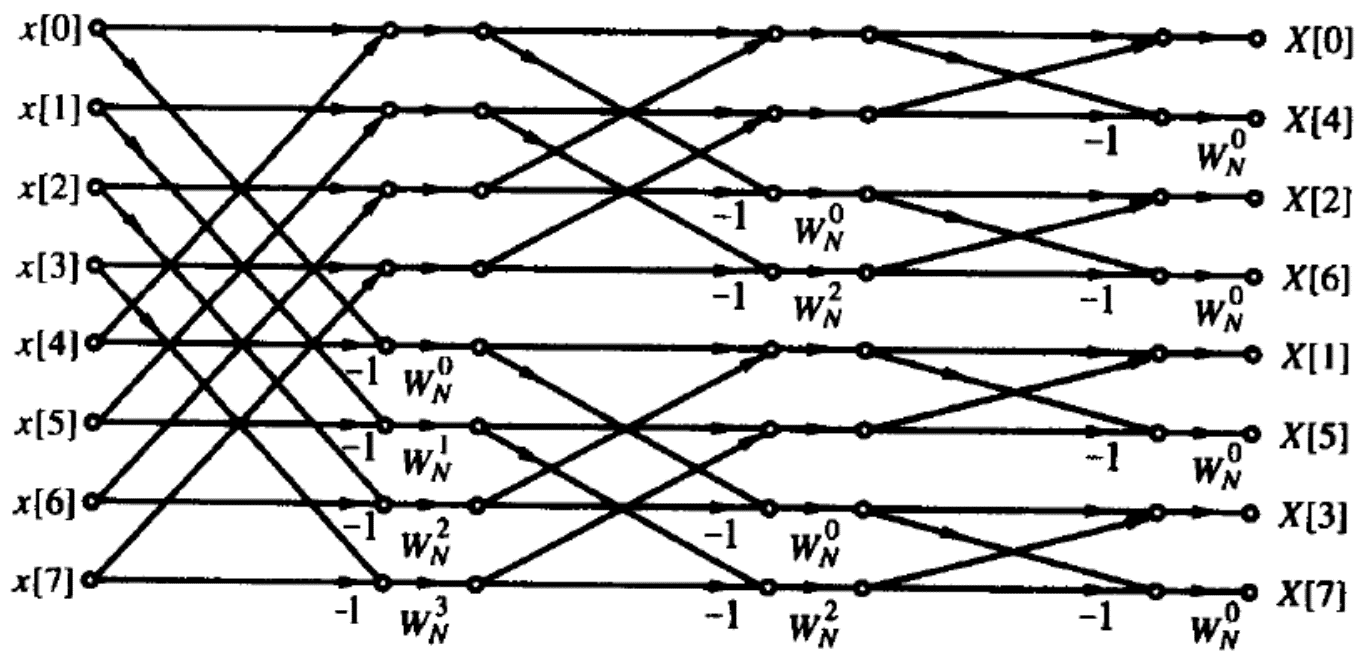
基4时间抽取FFT:
分为四组

N不满足要求需要补零
但是大量补零会影响实际效果

所以可以采用混合基,先用基3进行一次,分为3组,每组32个点,再进行基2,因为是2的五次方,不用补零,最后得到的依旧是96点的DFT
最后说一下FFT算法的应用,包含了5.9和5.10和11.3.4部分内容
11.3.4—计算N点IDFT,利用N点复序列DFT
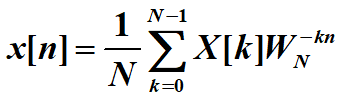
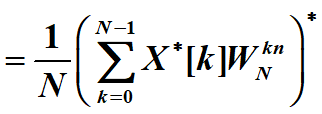
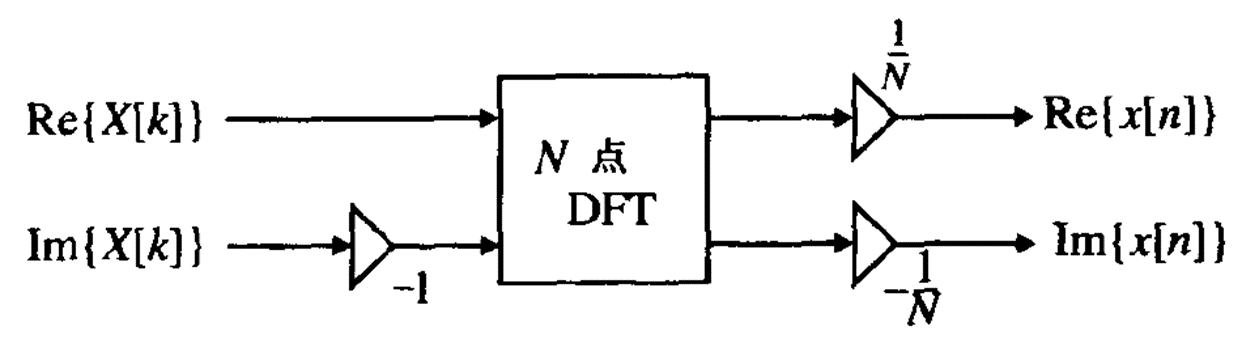
N点DFT改为N点FFT 看不懂
9.1 用单个N点DFT计算两个实序列的N点DFT
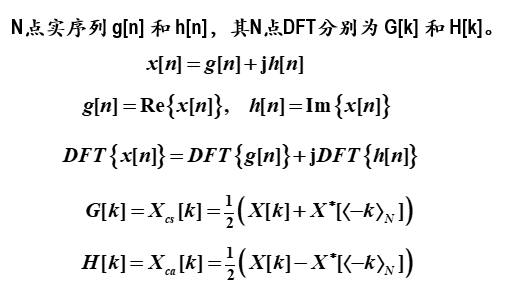
其实说应用也仅仅是把DFT改成FFT罢了,但是这块的核心是对称性质,实部分DFT对应共轭对称,虚部DFT对应是共轭反对称
9.2 用单个N点DFT计算一个实序列的2N点DFT
2N点的实序列假设为x[n]
定义N点实序列为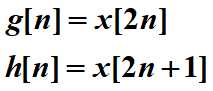 一个为偶序列一个为奇序列长度均为N
一个为偶序列一个为奇序列长度均为N
![]() 改为FFT
改为FFT
![]() 合二为一即单个N点序列
合二为一即单个N点序列
![]() 跟上面一样
跟上面一样
最后合成
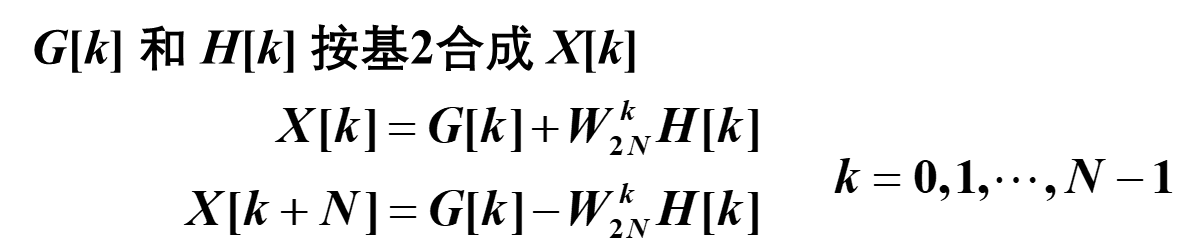
相当于把做了一次纯FFT计算而已,就是把x[n]分为奇偶然后各自做2N/2即N的DFT计算最后再合成,没了
5.10 用DFT实现线性卷积
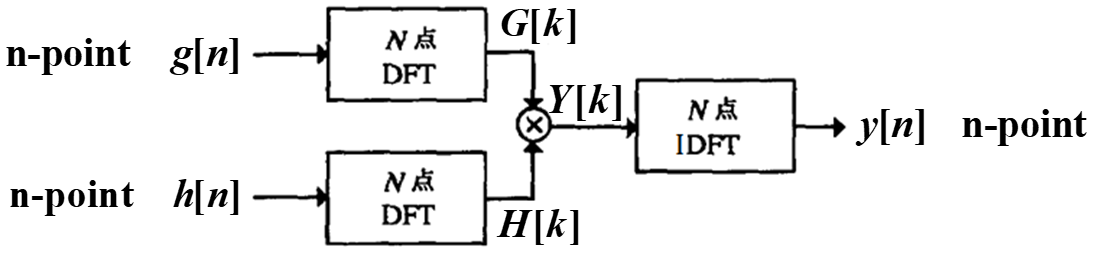
这是利用DFT的圆周卷积
利用圆周卷积的线性卷积需要补零
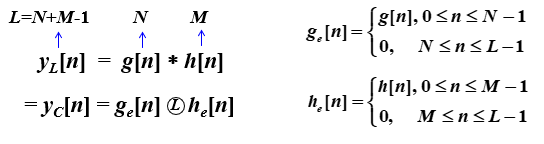
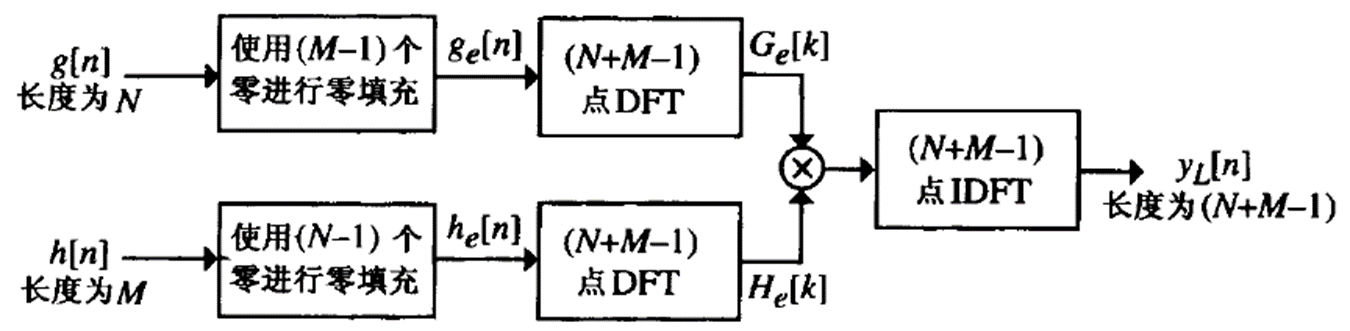
10.1 两个有限长序列的线性卷积
10.2 循环前缀
不要求
10.3 有限长序列和无限长序列的线性卷积
a.重叠相加法
b.重叠保留法

无限长的...不好说,看不懂


5.11 短时傅里叶变换
11.1 定义
11.2 在时间和频率维抽样
11.3 用matlab计算短时傅里叶变换
下面两个变换主要应用于信号压缩(应该不是重点)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号