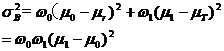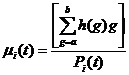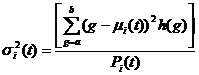全局二值化
目录
前言
二值化分为全局二值化和自适应(局部)二值化。在图像分析之前,通常需要将灰度图像二值化,再做进一步的分析。本文仅谈一些常用的全局二值化方法,简要地描述其思想并给出实现源代码(需要Opencv的支持),更为详细地关于原理的讨论可以在本文“参考文献”引用的论文找到。
Otsu(最大类间方差阈值)
理论
大津阈值又称为最大类间方差法[2],它是由Otsu在1979年提出的一种基于灰度直方图的阈值选取方法。它选取使类间方差最大的灰度级作为分割阈值,其具体思想如下:
设图像有L个灰度级,表示为[0,1, ... , L](通常L为255)。第i级的像素数量用ni表示,总的像素数量为N=n0+n1+…+nL。将灰度图像归一化,将其视为概率分布:
以第k级为阈值,将像素分成两类C0和C1(分别代表背景和目标,反之亦然);C0 表示属于[1,…, k]的像素,C1表示[k+1,…, L]的像素。
C0与C1表示的概率与均值:
ω0 = Pr(C0) = ![]() =ω(k) (2)
=ω(k) (2)
μ0 = ![]() Pr(i | C0) =
Pr(i | C0) = ![]() =μ(k)/ ω(k) (4)
=μ(k)/ ω(k) (4)
μ1 = ![]() Pr(i | C1) =
Pr(i | C1) = ![]() =(μT - μ(k))/(1 - ω(k)) (5)
=(μT - μ(k))/(1 - ω(k)) (5)
其中
ω(k) = ![]() (6)
(6)
μ(k) = ![]() (7)
(7)
容易证明,对任意k,均有以下关系式:
ω0μ0+ω1μ1=μT ,ω0+ω1 = 1 (9)
为了评价一个阈值的好坏,引入了差异分析[2]的差异准则,
其中
分别为类内方差、类间方差和图像的总方差。(11)的σ0和σ1分别表示C0和C1的方差,后面不会用到,故不再展开。
寻找一个能使λ、κ、η任意一个达到最大值的灰度级k就是要划分的阈值。![]() 是基于二阶矩的,而
是基于二阶矩的,而![]() 是基于一阶矩的。因此,计算η的最大值要更容易些,由于
是基于一阶矩的。因此,计算η的最大值要更容易些,由于![]() 是独立于k的,它等价于求
是独立于k的,它等价于求![]() 的最大值。
的最大值。
根据公式(2)-(7),可推出:
设k*为使η最大的最优值,则
这样就确定了图像的分割阈值。
大津法与后面将描述的Kittler方法在背景与目标能够在直方图区分开这个假设下都是最优的。
源代码
{
if (x < 0 || x >= img->width || y < 0 || y >= img->height)
return 0;
return img->imageData[y * img->widthStep + x];
}
inline void SetPixel(IplImage *img, int x, int y, BYTE val)
{
if (x < 0 || x >= img->width || y < 0 || y >= img->height)
return;
img->imageData[y * img->widthStep + x] = val;
}
#ifndef EPSILON
#define EPSILON 1e-6
#endif
/*
* Function:用Otsu(1979)阈值对图像二值化
* Parameters:
* [IN]img:要二值化的灰度图像
* [OUT]out:二值化的输出图像,要求调用者分配好空间
* Return:(None)
*/
void Otsu(IplImage *img, IplImage *out)
{
int hist[256], i, j, total, maxk;
float ut, uk;/*ut表示整个图像的均值*/
float p[256], sigma, wk, maxs;
/*得到灰度直方图*/
memset(hist, 0, sizeof(int) * 256);
total = img->width * img->height;
for (i = 0; i < img->height; i++)
{
for (j = 0; j < img->width; j++)
{
hist[GetPixel(img, j, i)]++;
}
}
/*计算大津阈值*/
ut = 0;
for (i = 0; i < 256; i++)
{
p[i] = (float)hist[i] / total;
ut += i * hist[i];
}
ut /= total;
wk = .0; uk = .0; maxs = .0;
for (i = 0; i < 256; i++)
{
uk += i * p[i];
wk += p[i];
if (wk <= EPSILON || wk >= 1.0f - EPSILON)
continue;
sigma = (ut * wk - uk);
sigma = sigma * sigma / (wk * (1.0f - wk));
if (sigma > maxs)
{
maxs = sigma;
maxk = i;
}
}
/*得到了阈值,对原图像分割*/
for (i = 0; i < img->height; i++)
for (j = 0; j < img->width; j++)
if (GetPixel(img, j, i) <= maxk)
SetPixel(out, j, i, 0);
else
SetPixel(out, j, i, 255);
}
Kittler(最小错误阈值)
理论
一幅图像的灰度直方图h(g)可以看成是由目标和背景两种像素组成的混合总体的概率密度函数p(g),g = 0,1, ..., T。假设它的每个分量p(g|i),i = 0或1,呈正态分布,并有期望![]() ,标准差
,标准差![]() 和先验概率Pi。
和先验概率Pi。
则
其中
Kittler的最小错误阈值思想是将灰度直方图分成任意两部分,用正态分布为每一部建模并将该模型与直方图比较。设第t级为阈值,它的每部分用h(g|i)建模,则它的先验概率Pi(t)、期望![]() 和标准差
和标准差![]() 分别为:
分别为:
和
其中
和
(8)
选择阈值t=t*,它使J(t)最小。[4]从熵的观点证明了该准则函数的合理性。
经过测试发现,Kittler在双峰特性比较明显,或者复杂背景下效果要比Otsu好。不过在直方图多峰的情况下,如下图,如果不做修正,Kittler得到的结果是非常糟糕的(阈值接近255),而用Otsu则效果很好。
Figure 1
Kittler在它的文章指出了如果在单峰情况下,阈值会出现在两端(0或255),在这种情况下,我们可以结合其他二值化处理,而Otsu则无法判别这种情况,总是将其分为目标与背景。因此,Kittler这个方法的另一个优点是它能够判定特殊情况而做相应处理。比如,论文中就利用该点对图像分块二值化,这种方法可以一定程度解决光照不均引起的图像退化。
最后,Kittler给出了一个求阈值的等式(它可根据Bayes最小错误分类的思想推导出来),用迭代法求解该阈值会比Otsu快,如果采用类似Otsu的方法,测试所有阈值,然后选取最小的,那么要比Otsu慢得多,因此它使用了二阶矩。迭代法也不是完美的,对初值的选定需要比较注意,以保证它收敛,对于上面举的多峰的例子,如果初值选在t=128的情况下,则会收敛到一个很好的结果。
源代码
源代码没有做任何优化,速度比较慢。其中EPSILON、GetPixel和SetPixel见Otsu的源代码
* Function:得到灰度直方图
* Paramters:
* [IN]img:要处理的灰度图像
* [OUT]h:直方图的存储地址
* Return;(None)
*/
void GetHistgram(IplImage *img, int *h)
{
int x, y;
memset(h, 0, sizeof(h[0]) * 256);
for (y = 0; y < img->height; y++)
for (x = 0; x < img->width; x++)
h[GetPixel(img, x, y)]++;
}
/*
* Function:用Kittler(1986)方法对图像二值化,本实现直接搜索整个直方图寻找最优阈值,
* 速度比较慢,根据Kittler(1986)的论文,可以使用迭代法快速计算。
* 公式J = 1 + 2[P0(T)log(sigma0(T)) + P1(T)log(sigma1(T))] - 2[P0(T)logP0(T) + P1(T)logP1(T)]
* Parameters:
* [IN]img:要二值化的灰度图像
* [OUT]out:二值化的输出图像,要求调用者分配好空间
* Return:(None)
*/
void Kittler(IplImage *img, IplImage *out)
{
int i, j;
int h[256], T = -1;
float P0, P1, u0, u1, sigma0, sigma1, J, minJ;
/*得到灰度图*/
GetHistgram(img, h);
/*计算阈值*/
minJ = 1e20f;
for (i = 0;i < 256; i++)
{
P0 = P1 = 0.f;
for (j = 0 ;j <= i; j++)
P0 += h[j];
for (j = i + 1; j < 256; j++)
P1 += h[j];
if (P0 < EPSILON || P1 < EPSILON)
continue;
u0 = u1 = 0.f;
for (j = 0; j <= i; j++)
u0 += j * h[j];
for (j = i + 1; j < 256; j++)
u1 += j * h[j];
u0 /= P0;
u1 /= P1;
sigma0 = sigma1 = 0;
for (j = 0; j <= i; j++)
sigma0 += (j - u0) * (j - u0) * h[j];
for (j = i + 1; j < 256; j++)
sigma1 += (j - u1) * (j - u1) * h[j];
if (sigma0 <= 0 || sigma1 <= 0)
{
if (T == -1)
T = i;
continue;
}
sigma0 = sqrt(sigma0 / P0);
sigma1 = sqrt(sigma1 / P1);
J = 1 + 2 * (P0 * log(sigma0 / P0) + P1 * log(sigma1 / P1));
if (J < minJ)
{
minJ = J;
T = i;
}
}
/*得到了阈值,对原图像分割*/
for (i = 0; i < img->height; i++)
for (j = 0; j < img->width; j++)
if (GetPixel(img, j, i) <= T)
SetPixel(out, j, i, 0);
else
SetPixel(out, j, i, 255);
}
结果对比
所有图像大小均为640*480,Canon Powershot S95拍摄:
(A)
(B) (C)
Figure 2(A)原图(B)Otsu (C)Kittler
(A)
(B) (C)
Figure 3 (A)原图 (B)Otsu (C)Kittler
(A)
(B) (C)
Figure 4(A)原图 (B)Otsu (C)Kittler
更多的测试结果请从这里下载。
结论
从测试的结果来看,Kittler和Otsu并不是很适合于对真实拍摄的图像二值化,Otsu的效果在测试结果中表现得更稳定些,不过噪声比较多。
参考文献
1、N. Otsu, 《A threshold selection method from gray-level histograms》, IEEE Trans. on Systems, Man, and Cybernetics, 1979
2、K, Fukunage,《Introduction to Statistical Pattern Recognition》, New York:
Academic, 1972, pp. 260-267.
3、J. Kittler and J. Illingworth.,《Minimum error thresholding》, Pattern Recognition, 1986.
4、Fan Jiulun and Xie Winxin,《Minimum error threshold:a note》, Pattern Recognition,1997