【BZOJ3894】【Luogu3358】文理分科 - 最小割多选一模型
链接Click Here
这个题就是个板子的最小割多选一模型啦\(QwQ\),这里介绍一种通用的解法。
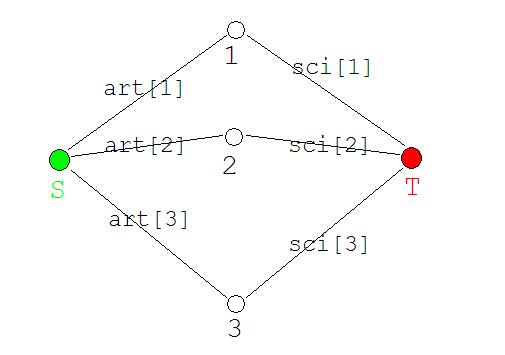
抛开组合收益不谈,这个题就是一个简单的最小割模型。我们只需要建出来这样一张图,在上面跑最小割,割掉的就是不用的,留下来的就是最大收益啦(≧▽≦)/,是不是很显然呢?
如果要考虑组合收益的话,我们把这个组合收益实体化成一个点来进行处理。还是上面那个图,我们假设\(2\), \(3\)是以和\(1\)四连通的两个点。这样的话我们需要保证一件事情:
-
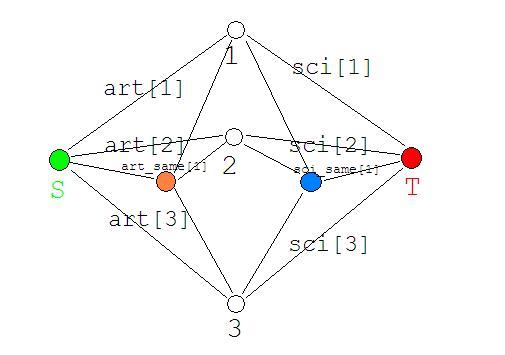
在\(art_1, art_2, art_3\)中,只要有一个被割掉(不选),那么\(art\)的组合收益就同时被割掉。
-
在\(sci_1, sci_2, sci_3\)中,只要有一个被割掉(不选),那么\(sci\)的组合收益就同时被割掉。
根据这些要求,我们建出来了下面这样的一张图。
很显然,这张图是可以满足上面的性质的。我们这样连边来看一下。
-
\(s -> art\_same(i, j)\) \(flow = art\_ex[i][j]\)
-
\(art\_same(i, j) -> linked\_nodes\) \(flow = INFF\)
思考一下,假如我们割掉了\(art\)中的任意一个,那么\(sci\)那边一定有对应的边没有割掉,这样我们的\(art\_same[1]\)就会顺着没有被割掉的边流走啦\(QwQ\)(也就是还是被割掉了\(QwQ\))
同理,理科那边和更多点的情况,这种图都是适用的。
关键需要注意的一件事情:在建图的时候,因为可能会出现\(art\_same[i]\)太大而另外一边的流量太小,无法完全割断的情况,我们要给它加上一个\(INF\),在最后求和的时候再减掉。而且这个\(INF\)一定要低于\(INFF\)的数量级,中间的边一定要保证是不能割掉的!这一点相当重要。
这种图是一种非常重要的最小割模型图,一定要会啊\(QwQ\)
#include <bits/stdc++.h>
#define N 30100
#define M 480010
#define int long long
using namespace std;
const int INF = 0x3f3f3f3f;
const int INFF = 0x3f3f3f3f3f3f3f3fll;
int n, m, art[105][105], sci[105][105];
int art_ex[105][105], sci_ex[105][105];
int node (int x, int y) {return (x - 1) * m + y;}
int same_art (int x, int y) {return n * m * 1 + node (x, y);}
int same_sci (int x, int y) {return n * m * 2 + node (x, y);}
int mv[5][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
bool in_map (int x, int y) {
return 1 <= x && x <= n && 1 <= y && y <= m;
}
int cnt = -1, head[N];
struct edge {
int nxt, to, f;
}e[M];
void add_edge (int from, int to, int flw) {
e[++cnt].nxt = head[from];
e[cnt].to = to;
e[cnt].f = flw;
head[from] = cnt;
}
queue <int> q;
#define fpop(x) x.front();x.pop()
int cur[N], deep[N];
bool bfs (int s, int t) {
memcpy (cur, head, sizeof (head));
memset (deep, 0x3f, sizeof (deep));
deep[s] = 1; q.push (s);
while (!q.empty ()) {
int u = fpop (q);
for (int i = head[u]; ~i; i = e[i].nxt) {
int v = e[i].to;
if (e[i].f && deep[v] == INFF) {
deep[v] = deep[u] + 1;
q.push (v);
}
}
}
return deep[t] != INFF;
}
int dfs (int u, int t, int lim) {
if (u == t || !lim) {
return lim;
}
int tmp = 0, flow = 0;
for (int &i = cur[u]; ~i; i = e[i].nxt) {
int v = e[i].to;
if (deep[v] == deep[u] + 1) {
tmp = dfs (v, t, min (lim, e[i].f));
lim -= tmp;
flow += tmp;
e[i ^ 0].f -= tmp;
e[i ^ 1].f += tmp;
if (!lim) break;
}
}
return flow;
}
int Dinic (int s, int t) {
int min_cut = 0;
while (bfs (s, t)) {
min_cut += dfs (s, t, INFF);
}
return min_cut;
}
signed main () {
memset (head, -1, sizeof (head));
cin >> n >> m;
int s = n * m * 3 + 1, t = n * m * 3 + 2;
for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> art[i][j];
for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> sci[i][j];
for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> art_ex[i][j];
for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> sci_ex[i][j];
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
add_edge (s, node (i, j), art[i][j]); add_edge (node (i, j), s, 0);
add_edge (node (i, j), t, sci[i][j]); add_edge (t, node (i, j), 0);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
add_edge (s, same_art (i, j), art_ex[i][j]); add_edge (same_art (i, j), s, 0);
add_edge (same_sci (i, j), t, sci_ex[i][j]); add_edge (t, same_sci (i, j), 0);
for (int k = 0; k < 5; ++k) {
int tx = i + mv[k][0], ty = j + mv[k][1];
if (in_map (tx, ty)) {
add_edge (same_art (i, j), node (tx, ty), INFF); add_edge (node (tx, ty), same_art (i, j), 0);
add_edge (node (tx, ty), same_sci (i, j), INFF); add_edge (same_sci (i, j), node (tx, ty), 0);
}
}
}
}
int ans = 0;// n * m * INF;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
ans += art[i][j] + sci[i][j] + art_ex[i][j] + sci_ex[i][j];
}
}
cout << ans - Dinic (s, t) << endl;
}