目录
-写在前面
-本文话题整体观
-概念(Concepts): 入门须知
-高度图(HeightMap)
-分形(Fractal)
-过程生成(Procedure Generation)
-地形纹理(Terrain Texture)
-细节纹理(Detail Texture)
-LOD(Level Of Details)
-算法(Algorithms): 魔术师的障眼法
-指导手册:《Focus On 3D Terrain Programing》
-随机分形地形算法
-地形纹理过程生成算法
-CLOD的遗憾
-实践(My Practices): 菜鸟也疯狂
-思路 / 采用Ogre作为渲染框架
-我的FTG( Fractal Terrain Generator )
-我的TMG( Texture Mapping Generator )
-结语
写在前面
阴霾了一周的天气终于在周末放晴。随着天气的好转,恼人的感冒似乎也逐渐离我远去了。在这个难得静寂而又悠闲的周末,我为怎样度过而犯难:一边是计划学习光照贴图(lightmaps)的知识,另一边却考虑好久没有系统总结下这一段时间学到的东西了。突然想起,孔圣贤有云“温故而知新”,顿悟。如果只顾向前疾驰,却不在意自己脚踩何处,那么很可能在某个不经意的清晨醒来后,发现那些曾经在心中熟透的知识已然乱作一团。于是我决定暂时安营扎寨,撰写一篇不会让自己遗憾的总结。如此,既可以作整理思维用,又可以建立自己的知识库,以备日后不时之需。
接下来,我在考虑这篇文章是写给谁的:显然,首先当然是给我自己的。但即便如此,我也不希望草草写下没有上下语境的技术记录。换句话说,我试图突破自己写技术文章时一些"发菜"的表现。我希望可以像科普作家那样,将晦涩的技术用通俗易懂的语言表达出来。这样,这篇文章可以有第二位服务对象:那些刚刚接触此技术的入门者。最后,我的终极愿望是,可以让完全不懂这个行业的读者明白我在说什么。为什么?——因为这可以向我的朋友证明,我的作文水平没有退步!嘿嘿。ok,泡杯咖啡,晒晒阳光,然后让我们开始!
本文话题整体观
本文是围绕图形学中的“地形”这个话题展开的。当然,如果全部涉及到是不可能的,我只讲我学到的东西。比如,你不会看到地形光照的内容,因为我还没学过。本文的重点是介绍利用过程生成技术生成地形纹理。但是我会介绍明白它所需要的必要知识。首先,我会在本文中介绍地形技术的一些基本概念,比如什么是高度图,什么是分形技术,等等。接下来,我会介绍一些学过的算法。有关“地形”的算法根据目的划分,主要有两类:一类是为了生成更加真实的地形而设计的算法;另一类则是为了优化渲染效率而设计的算法。但我只会着重介绍前者,而且会详细讨论如何生成地形纹理;对后者仅仅点一下。最后,我会讲述自己对这些算法的亲身经历,遇到的困难和解决方法,以及解释自己的代码结构等等。希望这样的布局不会让太多人反胃,我实在想不出什么更好的讲述之道了!
概念(Concepts): 入门须知
高度图(HeightMap)
如果你初次接触“高度图”,看到这个名字时会想到什么?不知道为什么,我会想起来读初中的地理课时,老师讲到的“等高线”那节内容。诚然,这里的高度图并非地理范畴的概念,但了解之后你就会发现,二者之间还是有点联系的。这里讲到的高度图,简而言之,就是一个盛放地形高度数据的文件。程度通过读取高度图中的高度数据,即可绘制出对应的地形。现在,让我们解释得更加形象一点。首先,让我们看看它长什么样子——哇,就是一张图片而已!没错,高度图是一个图片文件。至于是什么格式并没有规定,只要能盛放数据即可。bmp,jpg,tga,png….都可以。选择什么格式取决于你的程序中支持读取什么格式。现在你知道,图片除了做观赏用,还可以用来存储数据了吧。
现在让我们暂时切到另外一个话题,来谈谈图形学中顶点的显示。显而易见,对于任何一个有着高中教育背景的人,都可以想到,在三维笛卡尔坐标系中若要确定一点,一定需要3个数据:即分别x轴、y轴、z轴的分量。比如原点的坐标就是(0,0,0)。很好,现在考虑,假如你需要在一个已知区间内绘制一连串的点,比如连续5个点,你需要多少个数据?——是3*5=15吗? No,No。因为区间是已知的,对于每一个点,其x轴和z轴的分量都是知道的,因此只需要5个y轴分量的数据即可。ok,假设现在提供一个513*513的区间(也就是有513*513个顶点),你需要多少个y轴分量?没错,是513*513个。嗯?你发现高度图的图片尺寸也是513*513?呵呵,现在你明白高度图是什么了吧。它就是存储了一堆y轴数据而已。
如果用photoshop软件打开一张高度图,你会发现一组亮暗不一的阵列图(一般这是灰阶图)。这其中的亮暗不一的像素就代表了不同的高度。越亮代表越高,越暗代表越低。注意像素格式都是有边界限定的。如果设置了每个像素用1个字节(8位)存储,那么理论上限就是255;如果每个像素用2个字节(16位)存储,理论上限就是65535。
当实际绘制一张地形时,我们一般通过遍历一个与高度图同等大小的区间来绘制。每遍历一次,x坐标和z坐标的位置按顺序而更新,随后读取高度图中对应的y值分量,即可得到当前顶点的全部三个分量,该点即可被绘出。随后再遍历下一个顶点。随着遍历完整个区间,这张地形也就画出来了。
分形(Fractal)
由本人来解释分形的概念实在是惭愧,因为我对此也是一知半解。实际上“分形”这个概念在数学领域中相当复杂,你可以看到一堆的天文公式和看得头晕的理论。因此想要了解更多或者更准确的人可以关键字搜索百度或者google,一定会让你明白得更加透彻。这里简单讲一下我的认识。谈起分形,不得不提到那个有名的“曼德勃罗(Mandelbrot)集”。下面就是一张Mandelbrot集的图片。你可以看到,这张带有“分形”特点的图案有一个特征:无论放大多少倍,它的局部永远相似于它的整体。这个特征也可以被称为“自相似性”。举个例子,圆是分形图案吗?不是,因为圆的局部是某条非闭合曲线,而圆这个整体却是一条闭合曲线。常见的分形图案有,雪花,树枝等。注意,“自相似”不是“自相同”,局部并非是整体的完全复刻,差异是存在的。
曼德勃罗集
那么分形和地形有什么关系呢?实际上,起伏不平的山脉就表现为一种分形。从远处看,你可以看到高高矮矮的山峦参差不齐。如果把镜头拉近,你会发现即便在局部,它也是高矮不平的。因此,看到这里,你应该对我们的目的有一个大致的了解了:那就是要把分形技术应用到地形的生成上!下一节“算法”中,会进一步向你展示如何操作。所以,即便你已经内急,也请别走开,看下去,好戏就要上演了!
过程生成(Procedure Generation)
好吧,你还得再忍一会。如果你真憋不住了,那还是赶紧上个厕所先吧。因为理论一时半会还完不了。唔,我骗了你?嗯,那又怎么样?咬我呀咬我呀......
同样,我也无法给出“过程生成”这个词汇的准确涵义,推荐你在维基百科中查看它的介绍(这里)。个人的理解是,过程生成是一种依靠程序设定,按某种算法动态生成数据的一种技术。一般而言,这个技术和“分形(Fractal)”有很紧密的联系——经常是用“过程生成技术”来生成“分形”图形的,我们称这是一种“动态”生成的技术;与此相反的技术就是“静态”的技术,即如果需要制作某种图案,就提前用某种绘图工具将其制作好,然后传给程序使用。这种情况下这张图片是静态的,因为它是事先设计好的。简单一句话,计算机“算”出来的图片就是“动态”技术,人自己画出来的图片就是“静态”技术。
说到这里,高度图,分形,过程生成三个概念就可以统一起来了。我们绘制地形需要高度图数据。高度图可以事先人为地手工设计出来(就是画一个灰阶图),这就是静态方法;另一方面,刚才我们说过,由于地形是一种“分形”图案,它的形状符合分形的特征和规律,因此就可以利用“过程生成”的技术,用算法画出一个符合地形地貌的高度图出来。这就是动态方法。利用过程生成技术动态生成一个地形,不仅可以再现逼真的地形地貌,而且可以省去手工绘画的环节,大大减轻开发人员的负担。不过,这种技术并不是万能的。首先,要绘制的东西必须符合“分形”特征,其次,开发人员事先无法干涉会生成什么(不过也有解决这一问题的办法,只是算法稍微再复杂些),这对关卡设计人员不太是个好消息;最后,你还得忍受它特殊的风格——千篇一律!
地形纹理(Terrain Texture)
其实地形纹理没什么特别的地方,本质上它就是贴在多边形上的一张普通纹理。同其他普通纹理一样,它也是需要指定多边形的几个顶点和对应的纹理坐标,然后通过插值运算将纹理图案映射到对应的多边形上。一般而言,纹理图是需要单独手工制作的,就像前面提到的用“静态”方法制作的高度图一样。因为给模型(由许多多边形组成)贴什么样的皮肤,恐怕只有开发人员自己清楚。我来简单介绍一下普通的贴图方法:首先,用某种专业制作软件(比如3DSMAX),对照模型的多边形结构,绘制对应纹理;然后,将所有的纹理都集合在一张纹理图上,再为模型中的每个顶点指派一个这张纹理图的对应纹理坐标;最后,将这些既含有纹理坐标,又含有本身空间坐标的顶点输入给渲染API(DirectX或者OpengGL),API就会负责剩下的渲染工作,为你呈现出贴好纹理的模型。如此,那些模型看上去不再是赤裸裸的多边形了,而像贴了一层皮肤一样,向“逼真”迈出了伟大的一步。
但对于用“过程生成”技术生成的“分形”地形而言,事情似乎更困难了一点。很显然,你会发现,由于我们的地形是动态生成的,事先开发人员并不清楚会生成什么样的多边形——你看,连多边形都无法指定,纹理映射又从何谈起呢?这就是分形地形纹理的难点所在。然而,人类的智慧终究是伟大的,这个物种总是会时时刻刻给自己制造麻烦,然后又想出解决这些麻烦的方法,所为目的只有一个——让自己更接近于神!......ok,让我们回到话题。方法是有的,思路也很简单,既然高度图是可以“算”出来的,再“算”一张纹理图,又有何难呢?没错,你猜对了,分形地形的纹理图,也是用动态方法,也就是用过程生成技术生成的。酷吧!至于怎么生成,这仍然是下一节“算法”的保留节目,想知道的话就坚持看下去吧!
细节纹理
细节纹理是地形中的另一个话题。其实质是“多纹理(MultiTexturing)”技术。其实这是一个“多次采样并混合”的技术。渲染的时候,渲染API除了采集一般的地形纹理图的像素外,还会再采集一次细节纹理图,并进行混合,形成最终纹理贴在地表上。细节纹理使得地形更加真实,而没有细节纹理的地形看上去就像奶油一般嫩滑、不真实,当然会出现什么样的效果还得取决于你选用什么样的图案作为细节纹理图。
LOD(Level Of Details)
LOD中文翻译过来是“细节层次”,这并不是一个权威的定义,不过我觉得它比较好地反映出所指的技术。LOD技术在图形学中是一个大的话题,所涉及的不光是地形这么一个领域。宽泛地讲,它关注的是一种对任何模型都行之有效的优化技术。我来简单介绍一下它的由来,这样可以帮你更好地理解它是什么东东。我们知道,模型是由多边形组成的。多边形越多,这个模型就显得越圆润光滑;反之,模型就越粗糙有棱角(想象一个正六边形和正十二边形,哪个更贴近圆?)。那么我们是希望模型的多边形越多越好呢,还是越少越好?有位客官说,当然越多越好了,因为越多越逼真嘛,看现在的CG电影,哪个不是由成千上万的多边形组成的?也另有客官反驳说,不见得,越多虽然越逼真,但给处理器也带来了很大的负担。绘制一百个多边形和一百万个多边形,效率当然不可同日而语。二位谁说得对呢?
其实,都对。他们说的恰恰是我们所追求的两个指标:质量和性能。我们可以看出,这是一对互为矛盾的指标,任何一方的提升都要以对方的降低作为代价。因此,业界的尖峰话题也总是聚焦在“要求性能优良的同时要求画质精良”这一目标上。LOD技术就是关系到性能优化的一个技术。它的整体思路是通过降低模型的多边形数(也就是模型精度)来提升性能。但它的精巧之处在于,它有一个评估系统,根据评估标准划分出多个级别,级别越高就会采用越多的多边形表示模型,级别越低则模型多边形数量也越低。评估标准多种多样,这也是LOD核心的技术。可以举两个经典的例子:第一,根据“近大远小”原理,远处的物体总是看上去很小,这时即便它是一个复杂的多边形模型,人眼也无法分辨出它的细节,因此,可以对远处的物体采用较低的级别,降低其精度,减少绘制的多边形数量。近处的物体则用较高级别的LOD显示,满足质量需求;第二,对于起伏不大的表面(甚至一个平面),包含的多边形数量再多,其效果也是很有限的,而反之如果降低其多边形数量,所损失的精度也是很有限的,因此可以考虑降低级别,剔除多余多边形。而对于起伏较大的表面就可以采用较高级别的LOD绘制。我觉得,LOD技术正体现了孔圣贤的一句话:“大丈夫有所为,有所不为”——它其实是一种关乎选择的智慧。
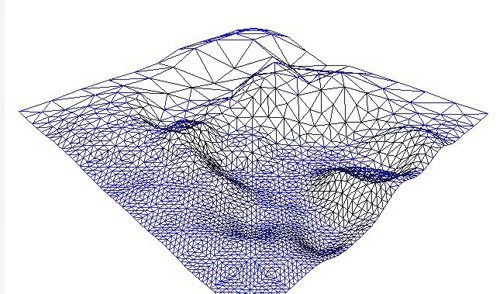
一个地形LOD的例子。你可以看到近处的网格非常密集,而远处则松散
现在,你应该了解LOD到底是什么东西了。好,讲了半天,终于可以回到地形话题上了。让我们看看地形中的LOD。没错,地形领域的一大研究课题正是LOD技术。尤其对于大型和超大型地形而言,其优化的必要更无需赘言。不过谈到地形中的LOD,我们往往谈到的是LOD技术的一个分支,就是在它的前面加个C字,叫CLOD(Continuous-LOD)。意思是“连续的LOD”。不过,这是什么意思呢?是扯到数学上的连续性了吗? 当然不是。实际上理解起来很简单,CLOD强调的是一种动态更新的LOD技术,它的更新频率就是帧频(也就是每刷新一帧,就会更新一次LOD)。这是因为,地形中的应用一般要满足“漫游”的需求(不可能画出地形,但不让人家操纵摄像机四周游览吧),因此视点可以自由移动和旋转,既然如此,也就无法人为判定地形中何为远,何为近了。很有可能在漫游的过程中,远处变成了近处,近处变成了远处。这样,就需要地形能够实时动态地更新自己的LOD层次,每一帧都要评估地形中哪些多边形拥有较高细节层次(近处),哪些拥有较低细节层次(远处)。由于每一帧都要更新,看上去LOD的切换就是“连续”的。因此,动态更新的LOD技术就是这里说的CLOD。
好了,讲了许多东西。终于把需要讲解的概念全部讲完了。我们介绍了高度图,分形,过程生成,地形纹理,LOD这几个概念。回忆一下,还对它们有印象吗?如果忘记了,最好回过头去再看一下。下一节,就会围绕这些概念讲述一些经典的算法。别走开,好戏开演! (这次是真的,没骗你...)
算法(Algorithms): 魔术师的障眼法
指导手册:《Focus On 3D Terrain Programming》
在这一节里,首先我要向你提起的就是这本大名鼎鼎的书,因为我通篇所讲的东西全部来自这本书。除此之外,我想所有混迹于游戏开发的人都不可能不知道它的作者:Andre LaMothe。这位大神同时也是《Windows游戏编程大师技巧》和《3D游戏编程大师技巧》的作者。最关键的是,这位大神还出奇得帅。。。在这个成天要与计算机打交道的行业里,才华横溢的同时能拥有这样的相貌,真是奇迹。
Andre LaMothe大神的语言幽默诙谐,知识解释得生动可爱,但又不乏通透准确;对知识体系的把握又深刻全面(如果想让我给出证明,请翻看《3D游戏编程大师技巧》的目录)。称他为大师真的是毫不为过。在我准备毕设的那段时间里,是他的《3D游戏编程大师技巧》把我带入了图形学的大门;现在当我研究地形时,又是这本书告诉了我有关地形的方方面面。除了向这位大师认真致敬一次外,我还能做什么呢?不过,对这个年代而言,依然有一些不尽人意之处,那就是——这几本书都比较古董了(《W》与《F》出版于02年,《3D》出版于03年),距今有六、七年之久。因此一些技术已经成为过去的经典。你可以因为这个原因而放弃它们,但我依然坚持向你推荐它们。
《Focus On 3D Terrain Programming》这本书是讲地形的专题。Andre在里面谈到了分形地形、地形纹理、地形光照等话题,还讲到了CLOD的三种经典算法:GeoMipMapping, QuadTree, 和改进的ROAM 。 最后他还涉及到一些相关话题:如水波,天空盒、 雾和基于相机的碰撞检测等等。我说过,本文的全部知识都来自这本书。因此我把它视作本文的指导手册,同时也认为是所有对这篇文章表现出了一点兴趣的人的指导手册。各位若想刨根究底,就去细心研读这本书吧!
随机分形地形算法
这一节是谈论如何用“分形”技术生成高度图的话题。对应前面谈到的“分形(Fractal)”的概念。讲述这个算法原本是个苦差事,不过幸运的是,我曾在以前写过这个专题。那是一篇我翻自国外某位技牛的文章,原文同样通俗易懂。你可以通过我的链接查阅原文。注意那又是一篇具有“相当长度”的文章,所以做一点心理准备较好。还有,看完以后,记得回来。
地形纹理过程生成算法
好了,这里才是我真正要付出心血的地方。咳咳,准备好了吗?让我们开始!
首先,允许我先笼统介绍一下该算法的大意:唔,你还记得我们的目的吗?没错,我们要为已经动态生成的高度图“配送”一幅恰当的纹理图。这幅纹理图应该也是动态生成的(过程生成),而且我们还要达到一种真实的效果——什么叫“真实”?在这个话题里,“真实”是这么定义的:地形中的山顶应该是白雪覆盖的(因为高处气温非常低嘛);山的中部应该长满了藏绿色的植被;再向下到了底部,应该以碎石、黄土为主。好吧,也许你并不认同这就是自然界“真实”的样子。没关系,暂且先让我们假设是这个样子。等你学会这个方法后,你可以随意操纵大自然,让它装扮成你希望的样子。
我们的算法不会复杂到要以真实的考虑因素去计算每一个像素。事实上,从上面的描述中你可以看到,我们只需把握住最重要的一点,就可以完成对大自然的模拟:那就是“高度”。不同的高度决定了不同的风貌。我们要做的就是针对纹理图中的每一个像素,采集到它所对应的高度,然后根据某种算法计算出它应该具有的像素值。而这种算法,就是我们要详细谈论的算法。别急,我先问问你,你知道如何采集纹理像素的“对应高度”吗?也许你已经有点眉目了。来,让我们一起大声说出来:“高度图!” 还记得吗,高度图中的每一个像素都代表了一个高度值。我们的采集方法就是按一定顺序读取高度图中的每一个像素值。
我认为,对学习任何算法而言,我们应该在脑子里明确一个供求关系:我们需要什么,我们能生产什么。将需要的东西转化成生产出来东西的方法就是算法。在这里,我们能够生产出一张纹理图,以供渲染API使用,这个你应该很清楚。那么,我们需要什么?我们需要一张高度图,和N张纹理图 —— 什么?需要的也是纹理图,而且还不只一张?究竟在搞什么东东?其实很简单,你可以这样想象,就像拿几瓶现有的香水,来“调制”出一瓶新的香水一样。这几张现有的纹理就是现成的“香水”,是原料;我们要根据算法和高度图数据来把它们“调和”在一块,得到的产物就是那张传说中的纹理图了。
如果你已经理解了我说的这些东西,那么解释剩余的算法就容易多了——无非就是这一思路的具体实现手段嘛。请让我拿一个具体的情境解释,这样你我都会轻松得多(呼...好累)。假设现在我们有四张现成的纹理图和一张已经动态生成的高度图。那么我们就是要,拿这张高度图,根据算法,调和那四张纹理图。而调和出的产物,就是最终的纹理图。对吗?如果还不明白,看看下面的图片,你就知道我在讲什么了。
这个算法我们需要关注三个方面。
好了。现在,我们不得不钻到每一个细节中去,看看一切究竟是怎么发生的。
1.如何为每一张现有的纹理图分配一个管辖的高度区域。
2.如何为一个指定的纹理像素计算像素值。
3.如何遍历纹理图。
1.如何为每一张现有的纹理图分配一个管辖的高度区域
假设我依次为现有的纹理图编号,顺序为:“黄土”--01,“草地”--02,“岩石”--03,“雪地”--04 。从前到后所对应的管辖高度区域越来越高。我们可以做一个最笨拙但也最简单的设计,比如纹理01的管辖高度域为0 — 60,纹理02的管辖高度域为61 — 120, 纹理03对应121 — 180,纹理04对应181 — 240。这样的布置就像排排坐一样,首尾相接,一目了然。不过,你可以猜想下这样的结果是什么——层次分明,中间没有任何过渡,导致效果极不真实。因此我们需要修改一下设计,怎样才能产生“过渡”的颜色?答案是“重合”。我们要让每一个纹理图的管辖高度与和它相邻的纹理图的管辖高度进行部分区域的重合,那些重合的区域受两张纹理图共同管辖。当我们生产新的纹理图时,如果纹理像素发现它采集到的高度值坐落在这个重合的区域,那么它的最终颜色就会受那两张纹理图共同的影响,计算出一个混合它们的颜色值(这实际上就是“调和”的过程)。
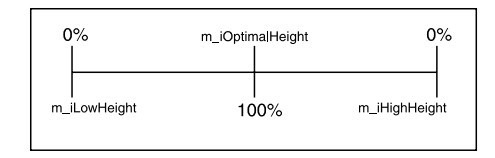
为了顺利达到这个目的,我们需要对每个管辖区域再定出三个边界点:低(low),适中(optimal),高(high)。这三个边界点把这片区域划分为两个区间:low - optimal和optimal - hight 。然后,我们做如下规定:高度恰位于optimal的顶点,其可见度为100%;随着顶点高度偏离optimal中心,其可见度也逐渐递减;当顶点高度位于low或者high时,其可见度为0% 。 如果有点糊涂,看下面的示意图会让你茅塞顿开。你也许不明白这么做有什么意义,没关系,等一下会举一个具体的例子,看了你就知道了。
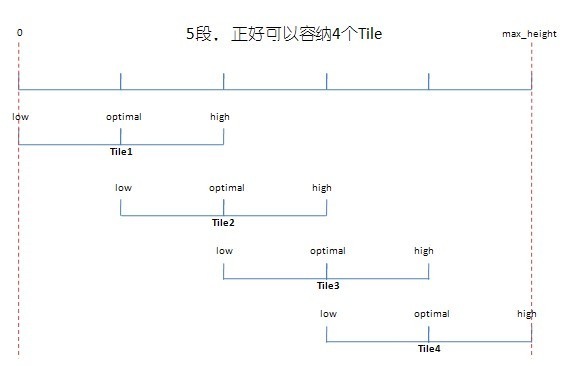
既然我们对“管辖区域”这个结构做了细致的规定,现在就让我们看一看如何“重合”他们——实际上简单的要命:每个管辖区域目前有了两个区间,重合的方法就是把低一级管辖区域的optimal - high区间与相邻高一级管辖区域的low - optimal区间重合。如此一层搭一层,就像搭楼梯一样。下面的示意图展示了明确的意思。
示意图
从上图中,你可以看到这个方法是如何影响我们的四块纹理图的管辖区域的。我统计如下:
纹理01的管辖高度为0 — 60,其中,low为0 ,optimal为30,high为60;
纹理02的管辖高度为30 — 90,其中,low为30,optimal为60,high为90;
纹理03的管辖高度为60 — 120,其中,low为60,optimal为90,high为120;
纹理04的管线高度为90 — 150,其中,low为90,optimal为120,high为150;
由于“重合”的计算规则,使得整体的覆盖区域比直接使用“首尾相接”的规则要短。因此你可以发现这时纹理01到04的跨度为0 — 150 (而之前的跨度是0 — 240)。
现在,还遗留下一个问题,那就是管辖区域的覆盖长度是如何决定的(上面的例子中,每个管辖区域的长度是60,然而我没告诉你为什么是60)。这个可以人为规定吗 —— 当然可以,上面的例子就是我随意规定的。但是,人为规定并不准确,因为你不知道使用多大的长度恰好可以覆盖地形中的全部高度。为此,我们需要一个计算方法来得知。其实也很简单,我们首先筛选出高度图中最大的高度值(对计算机而言这不是难事),假设为max_height,然后我们就知道整体的跨度为0 — max_height,整体的长度就为max_height。我们将这个长度除以比提供的纹理张数大1的数(这里有四张纹理图,所以是5)。得到的值就是每个纹理的管辖区域中的、每个区间的长度。注意,是管辖区域中的单位区间的长度,不是管辖区域本身的长度。这个例子中得到的值就是30。有了它,我们就可以算出具体该为每个纹理分配多大的管辖区域长度了,不仅如此,还同时可以算出其内部low、optimal、high的值。动动脑筋,找一张草稿纸来比划比划,这并不难。
你也许会问,为什么要除以“比提供的纹理张数大1的数”?
——我只能说,这样做可以让每一张纹理图的管辖高度都坐落在有效高度内;
原先的设计中我的确仅仅只除了纹理张数,
但后来我发现这么做会让最上面纹理图的管辖高度超出实际的有效高度。
在这里我还是建议你亲自试一下,把5换成4,然后看看会得到什么
现在我来举一个实际的例子,以便让你对上面的这些内容融会贯通。当然还是我们这个情境了。嗯,很顺利,我们在高度图中取到的max_height值恰好为150 —— 多巧啊!我们的纹理图现在有四张,所以除数为5, 150 / 5 = 30 。接下来,我们为每个纹理图分配管辖区域,其结果在上面我已经罗列出来。其实做完这一步,这个任务已经顺利完成了。但我打算再稍稍来一点“剧透”,让你明白那个百分比的意义。假设我在遍历过程中(第三步会详细讲如何遍历),对某一个纹理,从高度图里采集到的高度值是70 。 可以看到,70这个值坐落在了纹理02和纹理03的管辖区域内,属于“重合”的区域。那么就需要对这两张纹理都进行计算。对于纹理02,70大于optimal(60),因此纹理02在这点的可见度为(90-70)/(90-60)= 66%;对于纹理03,70小于optim(90),因此纹理03在这点的可见度为(70-60)/(90-60)= 33%。从表面上看我们也能观察出,70这个位置的确离纹理02的适中点近一些,而离纹理03的适中点远一些。因此纹理02的可见度就比纹理03的可见度大一些。你注意到没有,这两个可见度相加66%+33%=99%,正好接近1%。 实际理论上,相加结果恰好为1 。
2.如何为一个指定的纹理像素计算像素值
在这个环节我要解释的是,我们生产的纹理图中,每一个像素的颜色值最终是如何决定的。这要从像素的构成说起。你可能听过“三原色”的说法,如果你十分明白“三原色”和“像素”的关系,那就完全不用我多费唇舌了。但我假设你不太明白,所以稍稍解释一下。任何一个像素,都是由红色(Red),绿色(Green),蓝色(Blue)这三种颜色组成的。这三种颜色作为一个像素的颜色分量,其各自的比例影响着最终的颜色值。我们可以这么描述一个像素的颜色值:(R,G,B)。每个分量都有一定的上限,而计算机中,它们的上限是由位数(bit)决定的。比如每个分量有8位,这意味着红色有256级梯度,绿色也是,蓝色还是;三个分量合起来就是24位。也就是说一个像素需要24位的存储空间,合3个字节。当然还有其他的分配方案,比如红色5位,绿色6位,蓝色5位,合起来一个像素16位,合2个字节。因此,在我们这个算法中,决定一个像素最终的颜色值,实际上就是说决定该像素的RGB三分量的值。既然我们按这个规则来计算,那么解读提供的那几张纹理图的像素时,也应该是拆解成对应的RGB三分量分别读取了。
ok,现在说实质的东西。我用伪代码的形式把这个方法写出来。
遍历每一个将要生产的纹理图像素(现在当然是空的),对每一个像素:
找到对应的高度图中的位置,读取高度数据;
遍历所有提供的纹理图(这里是4张),对每一张纹理图:
根据高度数据,分析当前该像素在该纹理图中的可见度;
读取它对应位置的像素颜色(R、G、B三个分量值分别读出来);
用每一个分量值乘以可见度百分比,保存结果;
将这4张纹理图像素的计算结果相加,得到最终的像素颜色(R、G、B三个分量值);
把该像素颜色写入到将要生产的纹理图中的对应位置,完成一个像素的生产;
当做完这一切后,这张生产的纹理图也成功生成了。
继续拿上面那个例子做演示。上面我们已经计算出某像素的高度值是70,它在纹理02和纹理03的可见度分别为66%和33%。那么在纹理01和纹理04中呢?由于它不属于01和04的管辖区域,因此在它们中的可见度都为0% 。这样,按照规则,它应该读取纹理02对应位置的像素值,比如读出来是(30,20,10),乘以可见度66%,得(19.8,13.2,6.6);同样读取纹理03对应位置的像素值,比如(50,45,30),乘以可见度33%,得(16.5,14.8,9.9);纹理01和纹理04得到的结果都为(0,0,0)。最后,这个像素应该得到的颜色值为(19.8,13.2,6.6)+(16.5,14.8,9.9)+(0,0,0)+(0,0,0)=(36.3,28,16.5)。把这个值写入到纹理图的对应位置,完工。然后继续下一个像素值的遍历,重复该步骤即可。明白了吗?
3.如何遍历纹理图
在前面你不止一次听到我说“找到‘对应’的点”,但你依然一头雾水。这不怪你,因为我从来没讲过如何“对应”的问题。我把它留在这一节里讲。没错,这一节就是关注如何“对应”和如何“遍历”的问题。
就和我之前的风格一样,在正式开讲前,我总喜欢为你普及一点相关的知识(为什么我总喜欢把你当白痴呢...原谅我)。如果你认真看过我写在另一个地方的“随机分形地形算法”,你就会知道,一张高度图应该是个正方形,而且边长应该满足2^N+1的规律,因此高度图的尺寸应该为5x5,9x9 ,17x17,.... 513x513 。另一方面,纹理图一般也是正方形,且边长应该满足2^N的规律,比如纹理图尺寸可以为4x4,8x8,16x16,.... 512x512。 为什么纹理图是这样的规律?这是由于硬件的原因。把纹理图交给渲染API处理时,显卡硬件便接手此事。“纹理贴图”属于硬件渲染管线中的一个环节,而显卡做此操作时,要求提供的纹理图边长应该是2^N。至于说这又是为什么——这超出本文的范畴了。总之现在你明白了高度图和纹理图的尺寸规律:它们相似但却不同。
我们做一个简单的设计:让高度图尺寸和将要生产的纹理图尺寸符合“最佳匹配”。假设高度图的边长为2^N+1,那么我们就让纹理图的边长定为2^N 。比如,高度图尺寸是513x513,那么我们要求纹理图尺寸是512x512。这样,纹理图尺寸非常近似于高度图尺寸,贴图时的匹配效果最好。注意,这并不是最优化的设计,我们暂且先拿这个模型讨论,之后再做优化。现在你只要明白,一旦指定了高度图的尺寸,纹理图的尺寸也就指定了。我们这里假设纹理图尺寸就是512x512。那么我们就能开辟一个对应大小的内存空间,用来装载计算出来的纹理像素了。
我们还要注意下那几张当做“原料”的纹理图。它们的尺寸又该满足什么规律呢?——事实上,它们没有什么特殊的要求,因为它们并不会被送到渲染API中;更重要的是,它们没有必要和生产的纹理图一样大,它们可以采用更小的尺寸,比如,128x128或者256x256。当需要采集的像素位置超出它们的实际位置时,用一个简单的手法就能让它“绕回”到正确的位置上。见下图

通过简单的手法,当遍历到(0,256)点的时候,实际上就等于回到了(0,0)点。
这个简单的手法就是“余除”
好了,该讲的都讲到了,现在开始讲如何遍历。这才是关键。
我们分别用两个嵌套的循环,来索引生产的纹理图的位置。下面用伪代码表示。
对于纹理图中的每一行像素:
对于该行中的每一个像素(从左到右):
做某事
上面的写法应该很好理解。通过这种方式,我们就能索引到这张纹理图中的每一个像素,并为这个像素分配计算好的颜色。下面我们继续,看看如何“做某事”。
在“做某事”中,我们首先要找到对应的高度图位置。看,我又在讲“对应”了。如何对应呢?因为这张纹理图和高度图的尺寸非常相仿(前者512x512,后者513x513),我们直接到高度图取即可。比如对于纹理图中的(6,7)这个像素,直接到高度图中读取(6,7)这个像素的值。这么做虽然不够很精确,但已经相当不错了。所以不必担心太多。取到高度值后就可以用上面谈到的计算方法做进一步计算。还记得是什么方法吗?嗯,没错,我们要遍历提供的那几张纹理图,找到对应位置,对吧?不记得的话再返回去看一看。这里又有一个“对应”,这个“对应”该怎么匹配呢?由于要生产的纹理图尺寸和提供的作为原料的纹理图尺寸并不一样,因此我们不能直接取用。方法是之前提到的那个“聪明手法”,对,就是“余除”。通过这么一个小小的转换设计,就不用担心在取“原料”时超出范围啦!现在,我想所有一切都明了了。为了让你明白,我把该讲的都已经讲完了,现在用伪代码把所有东西串一遍:
(伪代码)
最后,我们讨论下优化的方案。
上面介绍的算法中,采用的纹理图尺寸是和高度图尺寸非常匹配的(只差一行和一列的大小)。但是,在指导手册中,它采用的纹理图尺寸和高度图并无什么关联,只要满足基本的2^N边长即可。这也意味着,可以任意决定生成的纹理图大小。这就是更好的方案。相比之下,上面的方法不仅非常简陋,而且牢牢和高度图尺寸绑定 —— 假如高度图是4097*4097,天啊,纹理图岂不是也要这么巨型?换句话说,优化方案可以令纹理图尺寸大大缩水,这样处理巨大地形时,纹理图不会大到让GPU吃不消的地步。
事实上,指导手册中方法的奥秘在于,它利用了“比例”的思想。对于一张并不匹配的纹理图和高度图,当纹理图遍历到某一个像素中时,根据该像素在本纹理图中的位置,找到高度图中等比例的位置的像素,然后读取它的高度值。当然还没有这么简单,这个方法还采用了“插值”的技术使得结果更加精确。至于具体怎么做,你可以查阅指导手册,也可以我在后面写的解释(这里)。
终于把这个可恶的算法讲完啦!我劝你好好休息一下,不要和自己过去,逼着自己看这篇又臭又长的写得乱七八糟的东东。写到这里时,已经过去了一个星期的时间。因此我也要休息一下,度过一个舒服的周末。另外,Merry Christmas!(虽然当你看到时早已经过去,但这的确是在圣诞节发出的祝福。这就是,时间的魔力)。
CLOD的遗憾
我原本的计划中,这一节打算涉及更多的东西:即详细讨论指导手册中讲到的CLOD的三种算法,Geomipmapping,QuadTree和改进的ROAM算法。而事实上你也看到了,我只认认真真写了一个算法。原因是,我发现自己没有能力和精力再写这些东西了...事情已经变得失控,我已经花了很多篇幅讲了一个尚且简单的算法,按照这个进度推测,当我写完那三个算法,恐怕要到明年的圣诞节了...这就是我的遗憾,非常抱歉。在我学习这三算法时,自己花了相当的精力来理解它们。印象最深刻的就是QuadTree让我一度头痛不已。我很想把自己所领悟到的细节写出来,却又一直拖延着,想等学习完所有的知识后再一起总结。现在才发现这不可能。那段记忆要么模糊,要么为如何表述它们而烦恼。关于算法我只能止于此。如果有合适的机会,我会重新回顾这三种算法。
不过,我可以稍稍介绍一些简单的事实:在图形学发展早期,由于CPU处理数据的能力比GPU强很多,那时设计的算法都是为了更多发挥CPU的机能,而尽可能减少GPU的占用周期。因此那时的做法都是用CPU去筛选多边形,把尽可能少的多边形交给GPU处理;而现如今,GPU的处理机能已经大幅上升,尤其是它的设计更适合处理浮点数。因此现在的策略都是尽量发挥GPU的机能,而让CPU负责尽可能少的工作(从而可以让CPU有能力负责其他的工作)。CLOD的三种算法中,GeoMipMapping是面向GPU架构的设计。而QuadTree和ROAM是面向CPU架构的设计。我个人的感觉是,指导手册花了更多的篇幅在介绍QuadTree和ROAM。但今天看来,GeoMipMapping才是更友好的算法。
实践(My Practices): 菜鸟也疯狂
思路 / 采用Ogre作为渲染框架
我从来没想过直接操纵底层API(不论是openGL还是DX)来实践这系列算法。因为这些算法关注的是“生成”,并非“渲染”。“生成”和“渲染”在实践中是完全不同的两个阶段。我们通过算法生成了一幅“高度图”和“纹理图”。至于如何渲染它们,则是你自己的选择。这从另一方面可以打消你对这些算法效率的担心——因为,即便效率真不怎么样,它们只影响到“生成”阶段。它们生成的其实是渲染用的资源,而这些资源你知道,只会在程序初始化时装载一次。这意味着它们对“实时渲染”这一阶段的效率压根没有任何影响。你所付出的代价仅仅是在初始化过程中又多等了那么几秒钟而已。
因此,我选择了Ogre作为实践的渲染引擎。这样,我可以专心思考如何写作“生成”算法,而把“渲染”的工作交给Ogre来完成。“Ogre是什么?”假如你如此问的话,那表示你还得需要花一段时间了解Ogre才能读懂下面的代码(其实真正和Ogre挂钩的只有那么几行)。Ogre是一款开放图形渲染引擎(Object-Oriented Graphics Rendering Engine),是一个包装了底层渲染API的上层建筑。如果你对Ogre比较陌生,我推荐你先了解下Ogre的场景管理器,并着重了解其中的“地形管理器”。因为我们用的就是它。对,仅此而已。
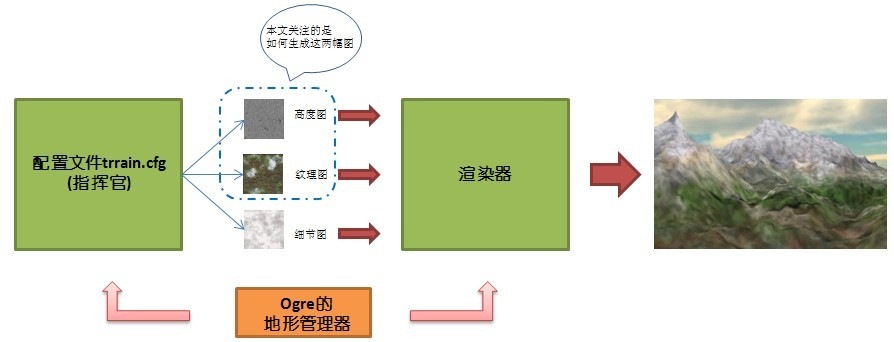
Ogre的“地形管理器”由一个配置文件和几张图片发挥作用。配置文件就像一个指挥官,它负责告诉地形管理器要用什么资源,以及资源的详细属性来生成地形。而几张图片就是所谓的“资源”文件了,它们由配置文件来指定。地形管理器需要三张重要的“图片”——高度图,地形纹理图,以及细节纹理图。看到熟悉的面孔了吗?没错,而那就是我们的目的。现在一切看来都很明了了:我们首先用算法分别生成一张“高度图”和一张与其匹配的“地形纹理图”,然后将其交给Ogre的地形管理器(细节纹理图不必修改,原有的就挺好)。再然后你就可以坐下来,好好欣赏一下由自己创造、并由Ogre渲染出来的地形了。
Ogre工作示意图
# The main world texture (if you wish the terrain manager to create a material for you)
WorldTexture=terrain_texture.bmp# The detail texture (if you wish the terrain manager to create a material for you)
DetailTexture=terrain_detail.jpg#number of times the detail texture will tile in a terrain tile
DetailTile=3# Heightmap source
PageSource=Heightmap# Heightmap-source specific settings
#Heightmap.image=terrain.png
Heightmap.image=terrain.raw# If you use RAW, fill in the below too
RAW-specific setting - size (horizontal/vertical)
Heightmap.raw.size=513
RAW-specific setting - bytes per pixel (1 = 8bit, 2=16bit)
Heightmap.raw.bpp=2# How large is a page of tiles (in vertices)? Must be (2^n)+1
PageSize=513# How large is each tile? Must be (2^n)+1 and be smaller than PageSize
TileSize=65# The maximum error allowed when determining which LOD to use
MaxPixelError=3# The size of a terrain page, in world units
PageWorldX=5000
PageWorldZ=5000
# Maximum height of the terrain
MaxHeight=5000
……
Ogre的配置文件:terrain.cfg
Ogre中对图片格式的支持相当全面。从bmp,jpg到png,raw一应具全。我真庆幸自己选择了这么一款强大的引擎。从实践的简单性考虑,我选择raw作为高度图的指定格式,bmp作为地形纹理图的指定格式。raw是最简单的灰度图格式,它没有任何文件头,从头到尾全是数据,因此特别适合于输出。bmp比较难点,不过我又偷了一个懒,使得自己一点都不担心它的输出问题。看到TMG一节时我会为你揭秘。
另外,提到LOD技术,Ogre中的地形管理器采用的是GeoMipMapping算法。前面提到过,这是一种对Gpu更加友好的算法。不过即便你不懂什么是GeoMipMapping也没关系,Ogre自己会处理得很好。
我的FTG( Fractal Terrain Generator )
接下来贡献的是我自己写的代码。这一节是关于“随机分形地形算法”的代码。FractalTerrainGenerator(分形地形生成器,以下简称FTG)是我创造的一个类。顾名思义,它的功能就是生成一张满足“分形”条件的地形(高度图)。
再见算法思想:
这可能让你恼火 —— 怎么又扯到算法上来了。 是呀,我比你还不情愿,可我想不出如何能逃过这一劫,却又能顺利地讲清楚下面的东西。放心,我不会再扯一大堆你已经知道的东西。这里我会结合代码来讲算法。
你已经知道,随机分形地形算法就是迭代地交叉计算“菱形”和“正方形”,我们称之为“菱形-正方形”算法。为此,需要一个结构来提供基本的支持。我设计的结构就是Squeare。Square类型实际上只有5个分量:左上、左下、右上、右下和中心,每一个分量值都代表这个正方形的角落值和中心值在mHeightDataBuffer数组中对应的索引位置。“菱形-正方形”算法是一轮一轮进行的。一个菱形阶段搭配一个正方形阶段看作一轮。在菱形阶段,利用所有的正方形计算出所有的菱形;在正方形阶段,则利用所有的菱形计算出所有的正方形。然后开始下一轮运算(又用新产生的正方形计算新的菱形)...直到mHeightDataBuffer所有的元素都被写入完毕。 在每个阶段,我们说的“计算”是指为这些正方形或菱形所指出的位置赋予一个高度值,然后存放在mHeightDataBuffer对应的元素中。
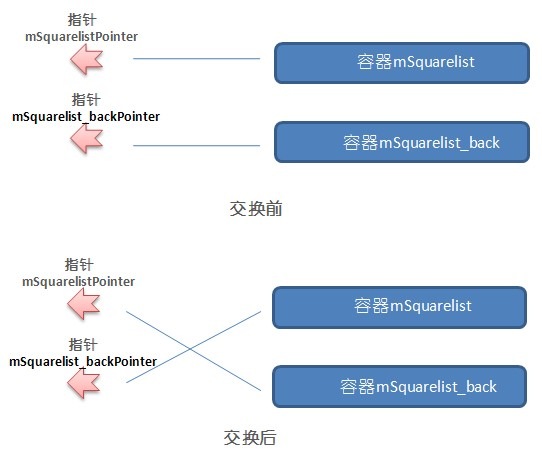
为了达到“一轮一轮”的目的,我设计了两个容器:mSquarelist和mSquarelist_back。前者是使用的容器,用来遍历已有的正方形;后者是后备容器,用来存放新生成的正方形。mSquearelist中的元素最初是没有中心值的,在每一轮回合中,通过“菱形阶段”的计算而使每一个正方形有了中心值(也就变成了菱形);在接下来的“正方形阶段”,再次遍历mSquarelist中的每一个元素,通过“正方形阶段”的计算而计算出了新的正方形。然后,把这些新的正方形压入 mSquarelist_back中。进行完一轮运算后,清空mSquarelist中的元素,并交换mSquarelist与mSquarelist_back的位置。这样就变成了mSquarelist_back为使用的容器,mSquarelist为后备的容器。然后开始新的一轮,反复进行下去。如何才能交换两个容器的位置?为此我又设计了两个指针,需要交换的时候,只要让指针的位置交换即可。也正因为如此,我觉得自己的设计很臃肿!(成员太多了,可一时又想不到别的办法。罢了,我不和自己较劲...)。
示意图
下面是该类的成员列表。
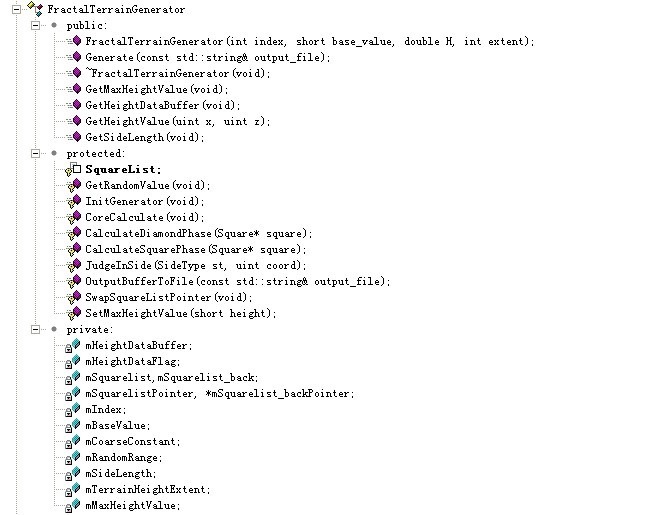
FTG成员列表
注意:我是按照翻译的那篇文章(就是我推荐给你的那个链接)而写的算法,
并非指导手册上的算法 .虽然它们其实讲的是同一个算法 .
如图中的列表所示,public中的方法是构造函数、析构函数和必要的公共接口,以及启动函数Generate(当然这也是接口)。protect中的才是算法的核心。它被封装在类的内部,使用户不必担心这些细节。最后private中的是类的全局变量,它们有的是旗标,有的是指定数据,有的则是存放数据的容器。
Private成员介绍:
mHeightDataBuffer:这是一个指向高度图缓冲区的指针。这个指针会指向一个(2^n+1)^2大小的数组空间,每个元素为short类型。short类型为有符号位16位bit,这表明高度图中的每一个高度值,最大值不超过2^15-1=32767 。这个高度已经足够大了。千万要注意的是,有符号位表示可以取到负数。但对于一张raw格式的高度图而言,最小值就是0。往这种格式的文件中存放负数,等待再次读取出来时会导致数据溢出(程序不会崩溃,但你会看到一个高得离谱的“突刺”)。因此一定要判断,假如计算的高度值出现了负数,就要更改为0 。
mHeightDataFlag:这是一个与mHeightDataBuffer有相同元素数量的数组空间,用来标记mHeightDataBuffer中每一个对应的元素是否已经写入。如果mHeightDataFlag[i]的值为false,则mHeightDataBuffer[i]的值就允许被写入;反之,则表示mHeightDataBuffer[i]中的值已经被写入了,那么它就不应该被再次写入(即不允许修改)。
mSquarelist, mSquarelist_back:用来盛放Square元素的队列。一个前备,用来遍历;一个后备,用来存放新结果。一轮运算下来,前后彼此交换位置。说到底它们存放的是一堆高度图缓冲区位置而已。我们只是将这个线性的位置形象地想象成一个方阵。
mSquarelistPointer, mSquarelist_backPointer:指向上面容器的指针。正是由于这两个指针,才能让两个容器彼此交换位置。
mIndex: 边长2^n+1中的n 。由构造函数的形参指定。
mBaseValue: 一开始四个角落值的初始值。由构造函数的形参指定。
mCoarseConstant: 粗糙度常数。2^(-H)的结果。而H由构造函数的形参指定。
mRandomRange: 随机值取值范围。由全局常量MAX_RANDOM_RANGE给出。
mSideLength: 边长2^n+1。计算得到。
mTerrainHeightExtent: 随机值范围的比例因子。由构造函数的形参指定。最终的随机值由取值范围的某值乘以该比例因子得到。相当于把随机值取值范围缩放了mTerrainHeightExtent倍。
mMaxHeightValue: 记录下在生成过程中最大的高度值。该值会在随后的TMG生成过程中使用。
Public成员介绍:
FractalTerrainGenerator( int index, short base_value, double H,int extent )
在实例化一个FTG对象时会调用构造函数FractalTerrainGenerator。当调用构造函数时,必须提供四个参数。如果你之前看了算法思想,就一定知道2^n+1代表高度图的边长。可以看到边长的大小直接取决于n的大小。这里形参index就代表n;base_value代表基准的高度值。这个值就是在最开始时提供给四个边角的值;H代表的就是那篇文章中提到的“粗糙度常数”的参数——它通过2^(-H)来决定每次循环时随机值取值范围应当缩减多少;extent是一个比例因子,通过它可以调节随机值取值范围的“跨度”。
构造函数除了将形参赋值给成员变量,还做了以下工作:将最大高度值初始化为-1;“种下”随机值种子;计算出边长值和粗糙度常数;将所有指针都置为空。不过构造函数并没有真正执行“初始化”的工作,它立足于能为每个成员变量都赋予一个值。真正的初始化放在了函数InitGenerator中。
2
3 mCoarseConstant=pow(0.5,H);
4 mSideLength=pow(2,mIndex)+1;
~FractalTerrainGenerator( void )
当FTG对象被销毁时会调用析构函数。像其他析构函数一样,这里它也仅仅负责一件事:安全释放动态申请的内存资源。成员中有两个指针指向了这样的内存块。因此会安全释放它们。
2 SAFE_DELETE(mHeightDataFlag);
注意:SAFE_DELETE是一个宏。其定义为:
#define SAFE_DELETE(x) { if(x){delete[] (x); (x) = NULL;} }
Generate( const std::string& output_file )
这是公共函数中最重要的方法了。因为缺少了它,你就无法启动这个类工作。该方法对使用该类的客户端开放。参数output_file指定要输出的高度图的文件名。在这个方法内部,依次调用protect域内的函数。调用次序为:InitGenerator(),CoreCalculate(),OutputBufferToFile(output_file)。从中你可以看出它的运行逻辑:首先初始化,然后进行核心计算,最后将得出的结果存放在指定的文件中。
2
3 CoreCalculate();
4
5 OutputBufferToFile(output_file);
Getxxx...
以Get开头公共函数都是作为其它类的接口。这里说的其它类,就是指TMG(Texture Mapping Generator)。因为TMG的工作需要FTG来提供,比如我们曾说过的“找对应的高度值”。有关TMG的内容放在下一节介绍。
Protect成员介绍:
GetRandomValue( void )
取得随机值。该随机值由mRandomRange, mTerrainHeightExtent和一丁点运气决定(要不怎么叫“随机”值呢)。
2
3 return random;
InitGenerator( void )
该方法执行真正的初始化工作。首先,它将容器指针与对应的容器绑定在一起;其次,申请一个存放高度图数据的空间(高度图缓冲区),配备一个存放“高度图数据是否被填充”的旗标空间,并初始化该旗标空间全部元素为假;再次,构建第一个Square,并把该Square插入到Square队列中;最后,将这个Square四个角落值对应的高度图缓冲区位置都填充为mBaseValue。
2 mSquarelistPointer=&mSquarelist;
3 mSquarelist_backPointer=&mSquarelist_back;
4
5 //1.申请一个存放高度图数据的空间,配备一个存放“高度图数据是否被填充”的旗标空间,并初始化该旗标空间全部元素为假
6 uint capacity=mSideLength*mSideLength;
7 mHeightDataBuffer=new short[capacity];
8 mHeightDataFlag =new bool[capacity];
9 memset(mHeightDataFlag, false, capacity*sizeof(bool));
10 memset(mHeightDataBuffer,0,capacity*sizeof(short));
11
12 //2.得到四个边角值,构建一个Square,并将该Square插入到Square队列中
13 Square* root_square = new Square(0, pow(2,mIndex), pow(2,mIndex)*(pow(2,mIndex)+1), pow(pow(2,mIndex)+1,2)-1);
14 mSquarelist.push_back(root_square);
15
16 //3.将根元素的坐标镶嵌到HeightDataBuffer中
17 mHeightDataBuffer[root_square->LeftTop]=
18 mHeightDataBuffer[root_square->RightTop]=
19 mHeightDataBuffer[root_square->LeftBottom]=
20 mHeightDataBuffer[root_square->RightBottom]=mBaseValue;
CoreCalculate( void )
这里执行的是核心的运算。最关键之处在于它定义了一个while循环框架。该循环会运行到mHeightDataBuffer中所有元素都已生成,才会结束。一次循环就是前面介绍的“一轮”运算。在循环体中,首先调用for_each来调用每一个容器元素参与“菱形阶段”(调用CalculateDiamondPhase方法)和“正方形阶段”(调用CalculateSquarePhase方法)(注意涉及到stl中的for_each算法和类内成员函数绑定的技巧,比较麻烦);完毕后,先清空使用中的容器元素,再调用SwapSquareListPointer方法交换两个容器先后位置;最后,缩小随机值取值范围。
2 {
3 //菱形阶段
4 std::for_each(mSquarelistPointer->begin(),mSquarelistPointer->end(),std::bind1st(std::mem_fun(&FractalTerrainGenerator::CalculateDiamondPhase),this));
5
6
7 //正方形阶段
8 std::for_each(mSquarelistPointer->begin(),mSquarelistPointer->end(),std::bind1st(std::mem_fun(&FractalTerrainGenerator::CalculateSquarePhase),this));
9
10
11 mSquarelistPointer->clear();
12
13 SwapSquareListPointer();
14
15 //缩小随机值取值范围
16 mRandomRange*=mCoarseConstant;
17
18 //Index值减小1
19 mIndex--;
20 }
21
22 mSquarelistPointer->clear();
CalculateDiamondPhase(Square* square )
传说中的“菱形阶段”。在这里,对每一个square计算其中心值的高度。并把此值存放到mHeightDataBuffer中对应的元素中。
代码略。
CalculateSquarePhase( Square* square )
传说中的“正方形阶段”。这里分两步:
1.计算square的四个次中心值(也就是菱形的中心值):top_center, bottom_center, left_center,right_center。求出它们的高度值,并存放到mHeightDataBuffer中对应的元素中。这里还要判断这四个值是不是位于最大正方形的四条边上(通过JudgeInSide方法)。如果是的话,那还要计算延伸到对面的点。此外,还要判断这四个值是不是已经求算过了。如果是的话,就要忽略掉。
2. 将新得到的四个正方形压入后备容器中。
代码略。
JudgeInSide( SideType st, uint coord )
判断给定的coord位置是否位于最大正方形的边上,st具体指出是哪条边:_TOP(上), _BOTTOM(下), _LEFT(左), _RIGHT(右)。不同的边计算方法不同。
2 {
3 case _TOP:
4 {
5 return ( coord - mSideLength < 0 ) ? true : false ;
6
7 }
8
9 case _BOTTOM:
10 {
11 return ( (coord + mSideLength) > (mSideLength * mSideLength -1 ) ) ? true : false ;
12 }
13
14 case _LEFT:
15 {
16 return ( coord % mSideLength == 0 ) ? true : false ;
17 }
18
19 case _RIGHT:
20 {
21 return ( (coord+1) % mSideLength == 0 ) ? true : false ;
22 }
23
24 default : break;
25
26 }
27
28 return false;
OutputBufferToFile(const std::string& output_file)
将mHeightDataBuffer缓冲区输出至文件。该文件就是raw高度图。output_file指明了文件名。
2 ofs.open(output_file.c_str(), std::ios_base::binary | std::ios_base::out | std::ios::trunc);
3 if(ofs.is_open())
4 {
5 ofs.write((const char*)mHeightDataBuffer, mSideLength*mSideLength*sizeof(short));
6 }
7 else
8 {
9 std::runtime_error("cann't open the output file when call OutputBufferToFile(). ");
10 }
11
12 ofs.close();
SwapSquareListPointer( void )
交换前后备square容器的位置。其实质就是交换mSquarelistPointer和mSquarelist_backPointer指针的位置。
2 sl_temp=mSquarelistPointer;
3 mSquarelistPointer=mSquarelist_backPointer;
4 mSquarelist_backPointer=sl_temp;
SetMaxHeightValue( short height )
这是一个简单设置mMaxHeightValue值的方法。将参数height与当前mMaxHeightValue值比较,谁大就保留谁为新的mMaxHeightValue。该方法会在每一次新的高度值产生后即可调用。
1 mMaxHeightValue = (mMaxHeightValue < height) ? height : mMaxHeightValue ;
实践收获:
1.注意灰度图的最小值为0. 你不应该将一个生成的负值存入高度图中,否则渲染出来会看到一个非常高的“突刺”。当生成新的高度值后,应该立刻检查它的符号:一旦为负,则将其归置为0 。 这个问题曾带给我无尽的痛苦,看着那一堆堆突刺满天的地形,程序却丝毫没有崩溃。我竟花了整整2天的时间来查找形成“突刺”的原因。惨遭蹂躏的2天啊...
2.随机值的取值应该调试好。是否能产生一个比较真实的地形,取决于随机值的好坏。
3.stl中的for_each算法并不能天然绑定类成员函数。因此需要bind1st以及mem_fun来帮忙。我不擅长stl,因此吃了很多苦头。总有一天我会找它们算账的。
我的TMG( Texture Mapping Generator )
这一节是关于“地形纹理过程生成算法”的代码。TextureMappingGenerator(纹理贴图生成器,以下简称TMG)是我创造的另一个类。这个类需要FTG才能工作,因此二者有很强的耦合性(主要是TMG非常依赖FTG,FTG并不需要TMG)。当然可以设计成TMG不需要FTG,取而代之去依赖一张高度图。这可以让FTG和TMG完全分开,彼此间没有任何联系。这样的设计虽然更加灵活,但却要付出额外的代价:那就是重新读取高度图数据到内存中,并筛选出最大高度值。这导致要遍历高度图数据起码两次以上。考虑到我的FTG和TMG本身就是为了协同工作而设计的,目前并无分开使用的打算。因此还是采用了耦合性很强的设计。 如此,高度图缓冲区可以直接利用,非常方便。
另外,由于TMG需要输入作为“原料”的纹理图(不仅是一块。由多块组成。为方便区分,以下称它们为Tile),还需要输出已经生成的纹理图。为了避免分散注意力研究“输入输出”这些东东,这一块的内容我直接采用了指导手册中的示例代码。导入了CIMAGE类操作相关事务。另外,CIMAGE还配备一个缓冲区用来存放纹理数据,因此也提供了数据的书写方法(这里的CIMAGE就相当于上一节那个简陋的高度图缓冲区)。可见CIMAGE的功能相当强大。根据CIMAGE的特性,我使用了tga格式作为输入的纹理图格式,而采用bmp格式作为输出的纹理图格式。
再见算法思想:
算法分两步:首先调用InitGenerator方法进行初始化工作,接着调用Generator方法生成纹理图。在初始化过程中,不仅要读入原料纹理图(通过LoadTilesFromFile方法),申请输出用的纹理图空间,还要为每个Tile分配相应的“管辖高度”(通过AssainTilesRange方法)。在生成过程中,要遍历输出用的纹理图,对于其中每一个像素,遍历所有Tile,根据可见度(通过CalculateTilePresent方法)调和其中的色度,最终把值累加到对应的输出像素中,并且保存在缓冲区中。最后,保存该缓冲区至文件即完成全部的工作。
下面是该类的成员列表
TMG成员列表
private成员介绍:
mTileNums:指示Tile的数量。由InitGenerator方法的形参指定。
mTileDataBuffer: 指向Tile数组的指针。数组中的每个类型都是CIMAGE。这里存放的所有TIle都是作为“原料”的纹理图。
mTextureDataBuffer:指向输出的纹理图的指针。它存放着最后生成的数据。保存到新的纹理图中的数据也来自这里。
mFTG:指向FTG的指针。这里即是与FTG耦合的地方。程序中需要FTG获得高度图的最大值和遍历时的高度值。
mTIleRangeArray:指向TileRange结构数组的指针。TileRange是一个有四个分量的结构体:{id, lowHeight,optimalHeight,hightHeight}。id表示该TileRange的序号,其余三个值就是前面算法中提到的,把管辖高度划分为两个区间的,三个边界点(见这里<链接>)。TileRange与Tile是对应的。但Tile本身存放的是纹理图信息,而它的管辖高度信息存放在了TileRange中。
public成员介绍:
TextureMappingGenerator( void )
TMG的构造函数非常简单,没有任何参数,而且函数体内没有做任何工作。这里构造函数得作用仅仅是初始化了所有的成员变量而已。指针置空,整型置0 。
~TextureMappingGenerator( void )
TMG的析构函数负责释放由成员变量指向的动态内存资源。别无其他。
InitGenerator( FractalTerrainGenerator* ftg, const std::string& base_name, int tile_nums )
这是TMG的初始化函数。负责初始化工作。与FTG的设计不同,这个函数也是开放给使用TMG的客户端使用的。也就是说,为了能够使用TMG,你必须首先自己调用这个函数完成初始化工作,然后才能调用Generate方法。参数中的ftg是要求提供的FTG,在这里将FTG与TMG绑定;base_name是指Tile的文件名基值。由于Tile不可能只有一个,为了能够顺利读取这些Tile资源,你需要将每个Tile命名成除了最后一个字符之外相同的名字,这个相同的名字就是基值。最后一个字符程序将自动根据数量用数字补其。最后的参数tile_nums表示Tile的数量。举个例子:假如读入的Tile有4块,而提供的基值是“texture_tile_”,那么程序真正读取的是文件名依次是“texture_tile_1.tga”,“texture_tile_2.tga”,“texture_tile_3.tga”,“texture_tile_4.tga”。
在InitGenerator方法中,读取了对应的tga纹理资源到Tile中,并且为相应TileRange分配合适的管辖高度。它是如何做到的?我们知道要分配合适的管辖高度,需要知道最大高度。而最大高度,就是从FTG中的GetMaxHeightValue方法得到的。
2
3 mTileNums = tile_nums;
4
5 mTilesDataBuffer = new CIMAGE[mTileNums] ;
6 if(!LoadTilesFromFile(base_name, mTilesDataBuffer))
7 {
8 std::runtime_error("can't load tiles from file");
9 }
10
11 mTextureDataBuffer = new CIMAGE;
12 mTextureDataBuffer->Create(mTilesDataBuffer[0].GetWidth() , mTilesDataBuffer[0].GetHeight(), 24);
13 //mTextureDataBuffer->Create(mFTG->GetSideLength()-1 , mFTG->GetSideLength()-1, 24);
14
15 mTileRangeArray = new TileRange[mTileNums] ;
16 AssainTilesRange(mFTG->GetMaxHeightValue(), mTileNums, mTileRangeArray);
Generate( const std::string& output_file )
该方法启动生成器工作,生成最终纹理,并输出纹理到指定的文件中,文件名为output_file。这是第二个开放给使用TMG的客户端的方法。当你调用InitGenerator后,就应该立刻调用这个函数。
这个方法是TMG运算的核心。它遍历每一个纹理像素,读取高度图缓冲区中对应的高度值,混合每个Tile的可见度,设置最终纹理的颜色值,最后保存纹理到文件中。
代码略。
Protect成员介绍:
LoadTilesFromFile( std::string base_name, CIMAGE* tiles )
读取“原料”纹理图片文件到Tile的方法。参数base_name是文件名基值,tiles表示Tile数量。base_name由InitGenerator函数提供,tiles由成员变量mTilesDataBuffer提供。
该方法是一个for循环的框架。在循环体内部,会依次为每一个Tile读取相应的文件。注意Tile的类型就是一个CIMAGE,因此读取的方法由它的成员方法LoadData指定。
2 {
3 std::string str = base_name + int2string(i+1) + ".tga";
4 if(!tiles[i].LoadData((char*)str.c_str()))
5 {
6 return false;
7 }
8 }
9
10 return true;
AssainTilesRange( short max_height, int tile_nums, TileRange* tr_array )
负责为每个Tile分配“管辖高度”,并保存在对应的TileRange中。参数max_height来自FTG中的GetMaxHeightValue方法。tile_nums来自成员mTileNums,tr_array数组则来自成员mTileRangeArray。

2 int height_current = height_unit ;
3
4 for(int i=0; i<tile_nums; i++)
5 {
6 tr_array[i].id = i+1;
7 tr_array[i].optimalHeight = height_current ;
8 tr_array[i].lowHeight = height_current - height_unit ;
9 tr_array[i].hightHeight = height_current + height_unit ;
10
11 height_current+=height_unit;
12
13 }
CalculateTilePresent( TileRange tr, int height_value )
计算当前高度(参数height_value)在当前TileRange(参数tr)的可见度。height_value由FTG中的GetHeightValue方法指定,tr由mTileRangeArray中遍历到的元素指定。
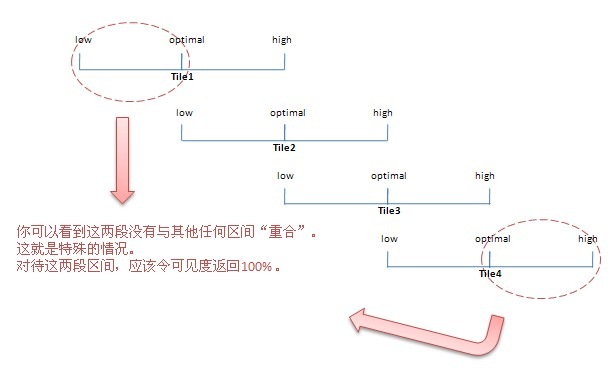
根据前面讲述的算法,对当前TileRange可以划分出两个区间。加上正好位于optimal点的情况,还有位于边界之外的情况,共有4种常规的情况,这4种情况计算可见度的方法不同。但是,还要考虑到另外2中特殊的情况:那就是位于最底部TileRange的low-optimal区间和位于最顶部TileRange的optimal-high区间。这两种情况的区间,由于没有其他的TileRange与它们重叠,如果按照常规规则计算的话,那么就会仅仅减少可见度而不再混合其他任何像素,导致出现像素颜色趋于黑色(亮度减弱)。因此对这两种特殊的情况,应该不允许减小可见度,也就是要令返回值为100%。
示意图

2 if(tr.id==mTileNums && height_value > tr.optimalHeight)
3 {
4 return 1;
5 }
6
7 if(tr.id==1 && height_value < tr.optimalHeight)
8 {
9 return 1;
10 }
11
12 if( height_value == tr.optimalHeight )
13 {
14 return 1.0;
15 }
16
17 else if( height_value < tr.optimalHeight && height_value > tr.lowHeight )
18 {
19 return (double)(height_value - tr.lowHeight) / (double)(tr.optimalHeight - tr.lowHeight) ;
20 }
21
22 else if( height_value > tr.optimalHeight && height_value < tr.hightHeight )
23 {
24 return (double)(tr.hightHeight - height_value) / (double)(tr.hightHeight - tr.optimalHeight) ;
25 }
26
27 else if( height_value <= tr.lowHeight || height_value >= tr.hightHeight)
28 {
29 return 0.0;
30 }
GetTexCoords( CIMAGE* tile, uint* x, uint* z )
这是处理对付任意Tile尺寸的一个简单方法。当提供的x和z坐标超出tile的实际坐标时,需要将xz坐标“绕回”到正确的位置上来。没什么复杂的东西,仅仅是用坐标去余除tile的尺寸即可。如此一来,你就可以提供任意的x和z坐标而不会发生任何“溢出”错误了。
2 (*z) = (*z) % tile->GetHeight();
GetInterpolatedHeightValue(uint heightmap_size,uint texturemap_size, uint unscaled_x, uint unscaled_z)
这是一个帮助你正确找到与纹理图像素对应的高度图像素值(即高度值)的方法。纹理像素根据自己在图中的位置,找到高度图中等比例位置的像素值,作为返回的高度值。这种方法可以提高读取精度。参数heightmap_size是高度图的边长,texture_size是纹理图的边长。unscaled_x和unscaled_z是纹理图的坐标位置,意为“未缩放的坐标”;在函数的内部,会算出一个“缩放后的坐标——scaled_x和scaled_z”,这是对应的高度图坐标,用这对缩放后的坐标到高度图中查找高度。注意,这里说的纹理图都是指输出用的纹理图,不是作为“原料”的纹理图。不要混淆了。
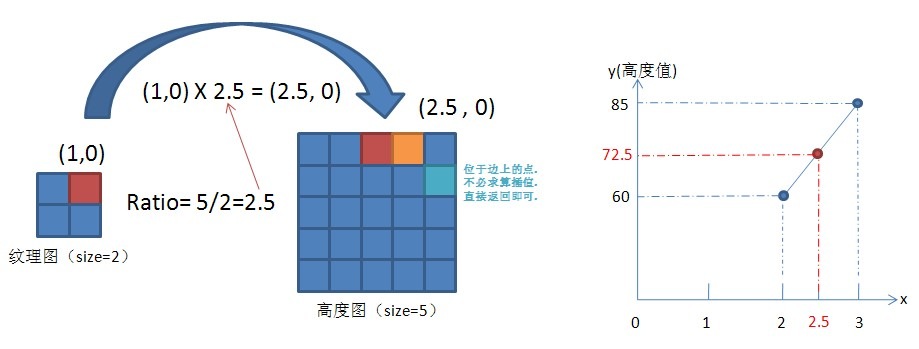
在函数内部,首先会算出一个比率ratio。ratio= heightmap_size / texturemap_size 。然后就算出了“缩放后的坐标”。(scaled_x,scaled_z) = (unscaled_x,unscaled_z) * ratio 。 但是,仅仅算出scaled_x和scaled_z并不能解决问题。因为,ratio往往不是整数(我使用的是double类型)。因此scaled_x和scaled_z很有可能是小数。但是,怎么可能找到带有小数坐标的高度值呢?要知道,高度图的像素都是一格一格为单位的。因此,这里还需要有个手段进行进一步的模拟——就是传说中“插值”。
我们知道scaled_x和scaled_z通常是带有小数的数。我们可以把它们拆成两部分:整数部分和小数部分。整数部分的坐标可以直接在高度图中取到高度值(标记为“起始点”高度);关于小数部分,将采用“线性插值”的办法计算得到——很简单,再向后读一个像素的高度值(标记为“结束点”高度),测量起始点和结束点的高度差,然后将该高度差乘以小数部分,就得到了相应的高度值。再将此高度值加上起始点高度值,就得到了插值的高度值。当然,为了提到精确性,需要分别向右(x轴方向)和向下(z轴方向)各读取一个像素,因此就要进行两次这样的插值计算。最后,求两次插值的均值,才是最终的结果。
这里得到的高度值既不是60,也不是80,而是计算出来的72.5
注意:这仅仅是x轴的。还需要对z轴做一遍相同的计算,最后求均值
在运算中还要考虑一种特殊的情况:当坐标位于纹理图的边界时(最右边或者最下边),那么就无法读取“后一个像素”了。这时,直接返回位于边界坐标对应的高度值即可。

2
3 double scaled_x = unscaled_x * ratio ;
4 double scaled_z = unscaled_z * ratio ;
5
6
7
8 double height_atinterpolate_x ;
9 if((uint)scaled_x+1 > mFTG->GetSideLength())
10 {
11 height_atinterpolate_x = mFTG->GetHeightValue((uint)scaled_x,(uint)scaled_z);
12 }
13 else
14 {
15 short height_atstart_x = mFTG->GetHeightValue((uint)scaled_x,(uint)scaled_z);
16 short height_atend_x = mFTG->GetHeightValue((uint)scaled_x+1,(uint)scaled_z);
17
18 height_atinterpolate_x = ( height_atend_x - height_atstart_x ) * ( scaled_x - (uint)scaled_x ) + height_atstart_x;
19
20 }
21
22
23 double height_atinterpolate_z ;
24 if((uint)scaled_z+1 > mFTG->GetSideLength())
25 {
26 height_atinterpolate_z = mFTG->GetHeightValue((uint)scaled_x,(uint)scaled_z);
27 }
28 else
29 {
30 short height_atstart_z = mFTG->GetHeightValue((uint)scaled_x,(uint)scaled_z);
31 short height_atend_z = mFTG->GetHeightValue((uint)scaled_x,(uint)scaled_z+1);
32
33 height_atinterpolate_z = ( height_atend_z - height_atstart_z ) * ( scaled_z - (uint)scaled_z ) + height_atstart_z;
34 }
35
36 short consequese = (int)(height_atinterpolate_x + height_atinterpolate_z) / 2;
37
38
39 return consequese;
实践收获:
1.我曾花了3天的时间来查找这么一种错误:纹理图生成了,看上去很逼真,可一旦贴在地表上,却总是不尽如人意:有的地方如同预想,高处为雪低处为土;但有的地方却不是这样,高处为土低处却出现了雪。这可怎么整?要知道引起这个问题的原因有千万中可能!我想了许许多多的方法来寻找问题到底出在哪里(包括下面说的一些调试方法,也缘于此)。我监视了每个像素的高度值、可见度、颜色值等等,并把它们输出到一个log文件中查看。最后,在我就要崩溃的瞬间,我想到了一种特别的方法来碰碰运气:用染色的方法来比对纹理图和高度图的异同,以此找出规律。我注意到高度图在非常低的地方像素颜色会很暗,因此我将纹理图对应的高度值低到一定程度(非常非常低)的像素都“染成”红色。然后我对比了两张图片。猜我看到了什么?——你一定无法体会当我看到它们时的惊讶和激动。

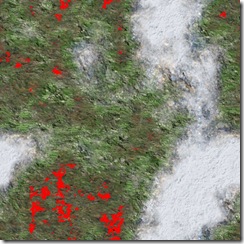

左:高度图 中:纹理图 右:将高度图垂直翻转后,与纹理图混合对比的结果。
从右图可以看出,二者的凹陷完全吻合
这时的结果再明了不过了。纹理图与高度图的方向竟然互相垂直反转!这是什么原因造成的?我突然想起了纹理图是一张BMP格式图片,而高度图是一张RAW格式图片。经过思考,终于明白了是由于特定图片格式的读写顺序不同造成的差异:RAW是从左到右、从上到下的写入顺序,因此它的原点坐标在图片的左上角;而BMP却比较特殊,它是从左到右,从下到上的写入顺序,因此原点坐标在图片的左下角!因此在写入纹理图像素时,一定得注意正确的z轴方位,先写最后一行,最后写第一行。ok,让我们问候微软全家以及他们的祖宗吧...
2 mTextureDataBuffer->SetColor(x,side-1-z,(unsigned char)red_data,(unsigned char)green_data,(unsigned char)blue_data);
2.再次注意溢出。在调试GetInterpolatedHeightValue时,又发生了意想不到的错误。在很高的地方竟然齐刷刷地用黄土纹理覆盖了。根据多次遭蹂躏的经历,我很直觉地感觉到这又是一起“溢出”事故。用log输出数据——果不其然!那么,在这个方法中,到底哪里溢出了呢?看下面的代码
1 short consequese = (short)(height_atinterpolate_x + height_atinterpolate_z) / 2;
1 short consequese = (int)(height_atinterpolate_x + height_atinterpolate_z) / 2;
从中可以看到,在很高的地方,两个非常大的16位数相加,会导致结果超过2^16,但如果依然用16位存储中间结果,就会造成数据溢出,表示成负数。对于负数的纹理,程序当然会按照最下层Tile的low-optimal对待了。因此就变成了黄土纹理。只要改用较大的数据存储就不会溢出,被2除之后又会回到2^16的范围内,这时就还能用short类型存储了。
3.条件编译与调试。为了得到调试信息,我写了一个方法,用来专门输出调试数据(每个像素的高度值、可见度、颜色值等等)。但是,输出这么一个海量的数据,其等待时间不是一时半会的。我一会想看数据,一会又想看效果,怎么办?总不能看数据时写上输出log的代码,看效果时再删掉吧。我采用了“条件编译”的小技巧,看数据时就定义指定宏,看效果时就删掉这个宏。方便至极! “条件编译”真的是调试程序的必备手段啦!

2 //输出数据
3 OutputDataLog("--------------","--------------");
4 OutputDataLog("tile id:",tr_array[i].id);
5 OutputDataLog(" tile low_height:",tr_array[i].lowHeight);
6 OutputDataLog(" tile optimal_height:",tr_array[i].optimalHeight);
7 OutputDataLog(" tile hight_height:",tr_array[i].hightHeight);
8 OutputDataLog("--------------","--------------");
9 OutputDataLog(" "," ");
10 #endif // _DEBUG_OUTPUTDATA
11
4.模板的利用。我从来没有写过模板与泛型的东西(我从来不掩饰自己是菜鸟),直到我写输出调试数据的方法时。我想达到一种效果,就是提供的参数不要指定是什么类型,因为我需要输出各种各样的类型(string,int,short,double等等)。这时模板帮了我大忙。第一次体会到模板的强大,还等什么,写字留念~

2 inline void OutputDataLog(const std::string& tip_text, T data )
3 {
4 if(ofs.is_open())
5 {
6 ofs<<tip_text;
7 ofs<<" : ";
8 ofs<<data;
9 ofs<<std::endl;
10 }
11 else
12 {
13 std::runtime_error("can't open file: data_log.txt ");
14 }
15
16 }
结语:
我真的不想再浪费一滴口水在这篇文章上了。从此以后我也要慎重考虑,是否再写类似这样的冗长的臭文了。最后我要对你表示感谢,因为你能坚持看到这个地方,简直可以算做我的粉丝(或者偶像,知己...随便怎么称呼)。感谢你对我劳动成果的尊重,我也希望本文对你有帮助。如果你考虑转载请附上原文链接谢谢。同时我会把它视作我对学过知识的总结,以防落得没人看出现的尴尬.....好了,让我们赶紧结束它吧。再见。


















 浙公网安备 33010602011771号
浙公网安备 33010602011771号