堆排序(概念、原理、实现)
完全二叉树的定义、性质以及算法见正文,这里补充一点:完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,几乎每次都要考到的二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
1 判断完全二叉树
完全二叉树:除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点。
2 完全二叉树定义
完全二叉树(Complete Binary Tree)
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
一棵二叉树至多只有最下面的两层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,则此二叉树成为完全二叉树。
3 完全二叉树特点
叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或 L+1;
出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:
tree[n]: int {tree[0], tree[1]...tree[n-1]}
对于tree[i],有如下特点:
(1)若i为奇数且i>1,那么tree的左兄弟为tree[i-1];
(2)若i为偶数且i<n,那么tree的右兄弟为tree[i+1];
(3)若i>1,tree的双亲为tree[i div 2];
(4)若2*i<=n,那么tree的左孩子为tree[2*i];若2*i+1<=n,那么tree的右孩子为tree[2*i+1];
(5)若i>n div 2,那么tree[i]为叶子结点(对应于(3));
(6)若i<(n-1) div 2.那么tree[i]必有两个孩子(对应于(4))。
(7)满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
完全二叉树第i层至多有2^(i-1)个节点,共i层的完全二叉树最多有2^i-1个节点。
4 算法
如果一棵具有n个结点的深度为k的二叉树,它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应,这棵二叉树称为完全二叉树。
可以根据公式进行推导,假设n0是度为0的结点总数(即叶子结点数),n1是度为1的结点总数,n2是度为2的结点总数,由二叉树的性质可知:n0=n2+1,则n= n0+n1+n2(其中n为完全二叉树的结点总数),由上述公式把n2消去得:n= 2n0+n1-1,由于完全二叉树中度为1的结点数只有两种可能0或1,由此得到n0=(n+1)/2或n0=n/2。
总结起来,就是 n0=[n/2],其中[]表示上取整。可根据完全二叉树的结点总数计算出叶子结点数。
5 小根堆
小根堆一般指最小堆
堆是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于(或不小于)其左孩子和右孩子节点的值。(注意,这里对同兄弟结点没有要求)
最大堆和最小堆是二叉堆的两种形式。
最大堆:根结点的键值是所有堆结点键值中最大者。
最小堆:根结点的键值是所有堆结点键值中最小者。
而最大-最小堆集结了最大堆和最小堆的优点,这也是其名字的由来。
最大-最小堆是最大层和最小层交替出现的二叉树,即最大层结点的儿子属于最小层,最小层结点的儿子属于最大层。
以最大(小)层结点为根结点的子树保有最大(小)堆性质:根结点的键值为该子树结点键值中最大(小)项。
6 原理过程
如何建立这个堆呢。可以从空的堆开始,然后依次往堆中插入每一个元素,直到所有数都被插入(转移到堆中为止)。因为插入第i个元素的所用的时间是O(log i),所以插入所有元素的整体时间复杂度是O(NlogN),代码如下:
1 n=0;
2 for(i=1;i<=m;i++)
3 {
4 n++;
5 h[n] = a[i];
6 siftup();
7 }
其实我们还有更快得方法来建立堆。它是这样的。
直接把整数放入一个完全二叉树中(这里我们还是用一个一维数组来存储完全二叉树),然后通过直接的堆调整来完成排序,如下图(注:这里的图片来自哈工大李建中《算法设计与分析》课件)
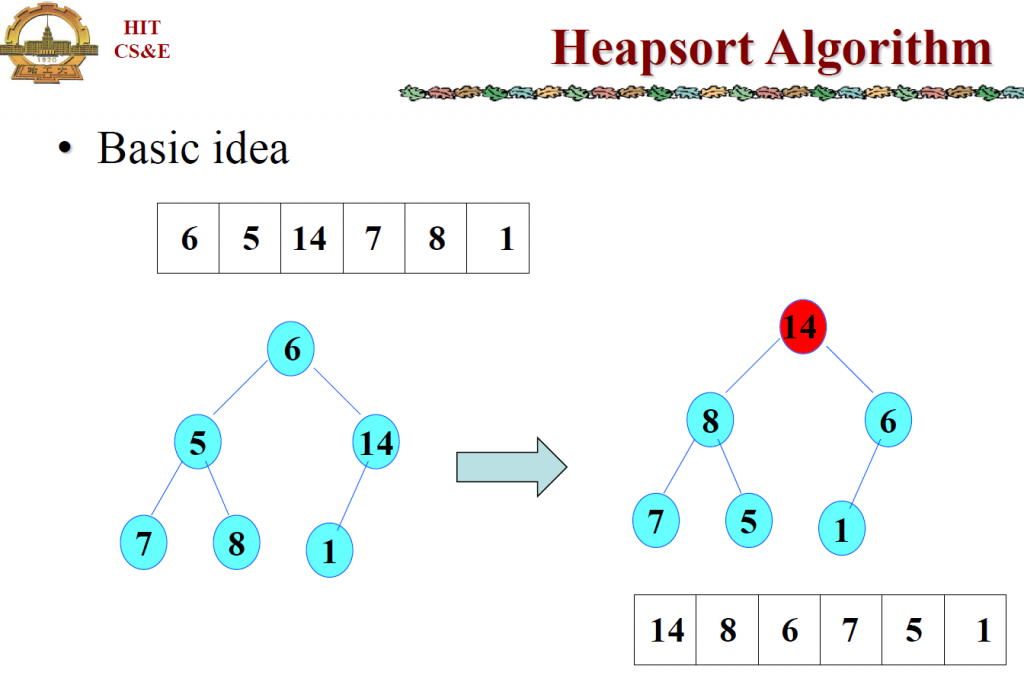
现在要完成6个整数{6,5, 14,7, 8, 1}的大根堆排序;
这里左侧是建立完全二叉树,然后调整为大根堆结构; 开始的位置是第一个非叶节点及其子节点;
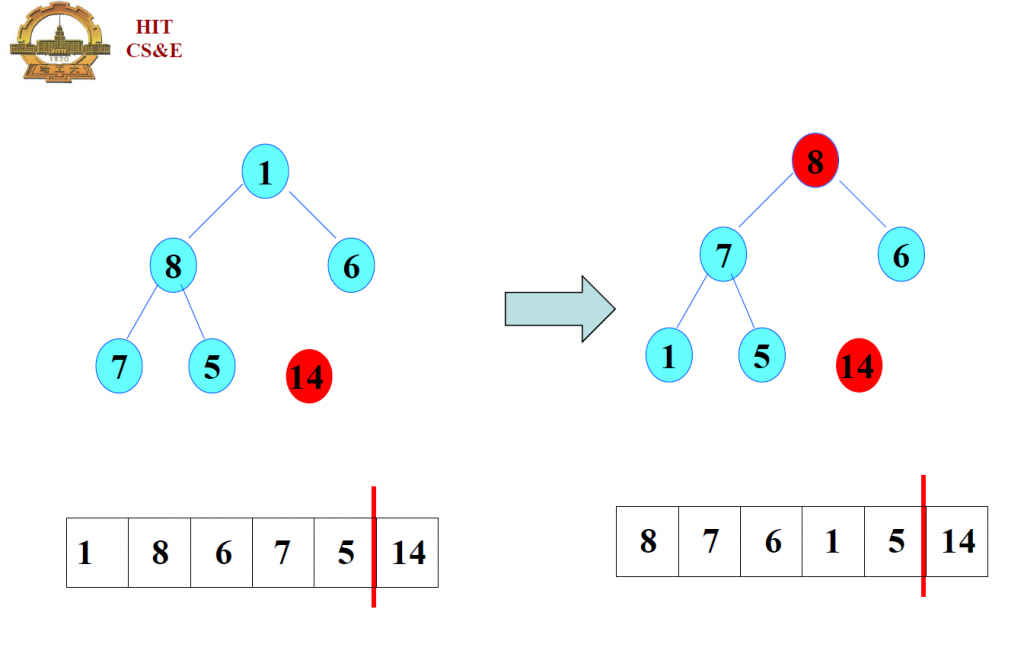
上图是要排序时,将大根堆的根节点(这里是14)从二叉树中去掉,然后用最后一个叶子节点(这里是1)填充,变成了上图左侧的结构, 然后再调整为大根堆,就是上图右侧二叉树;
下面几幅图操作相同.
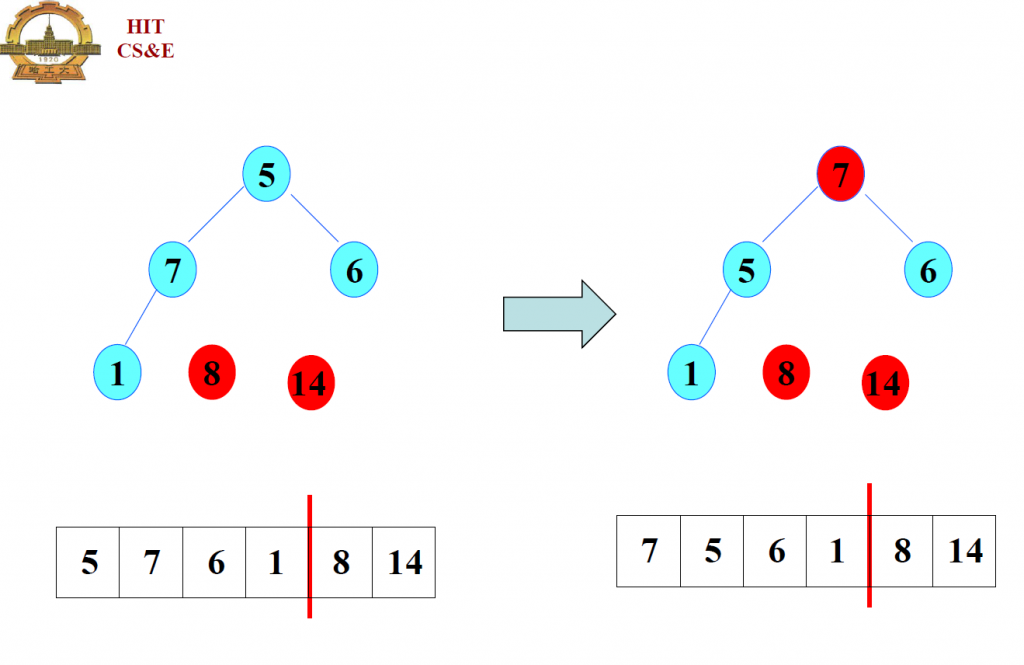
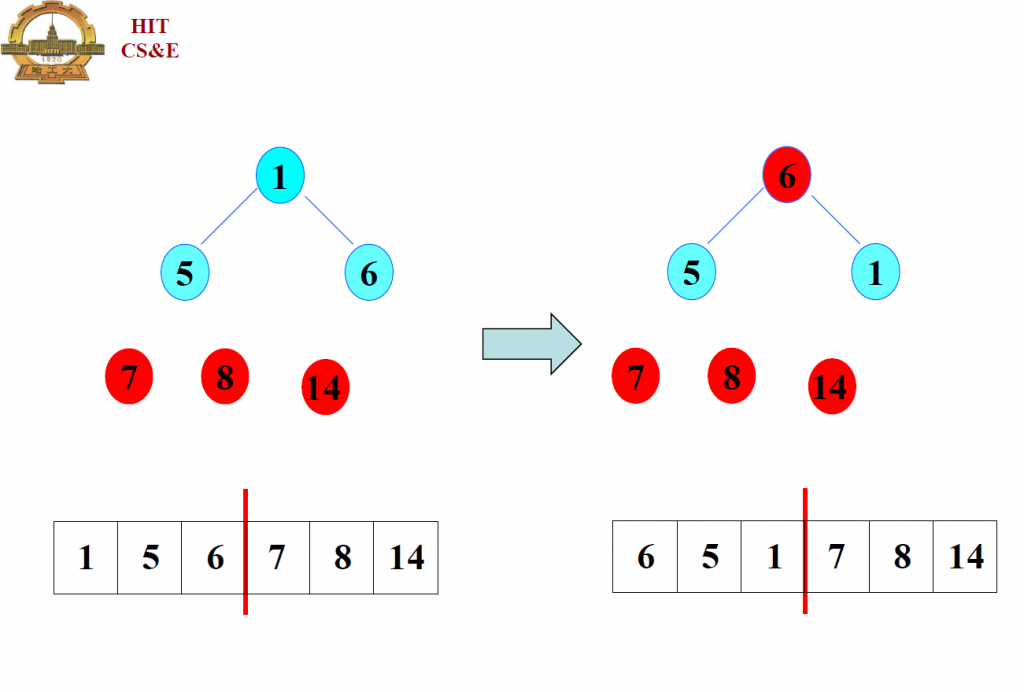
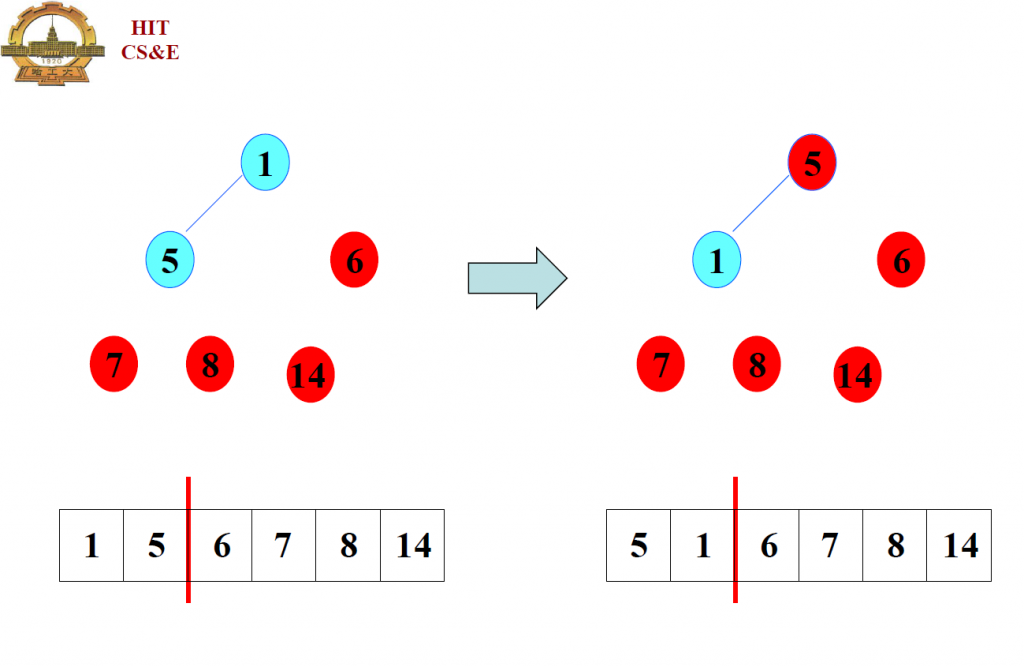
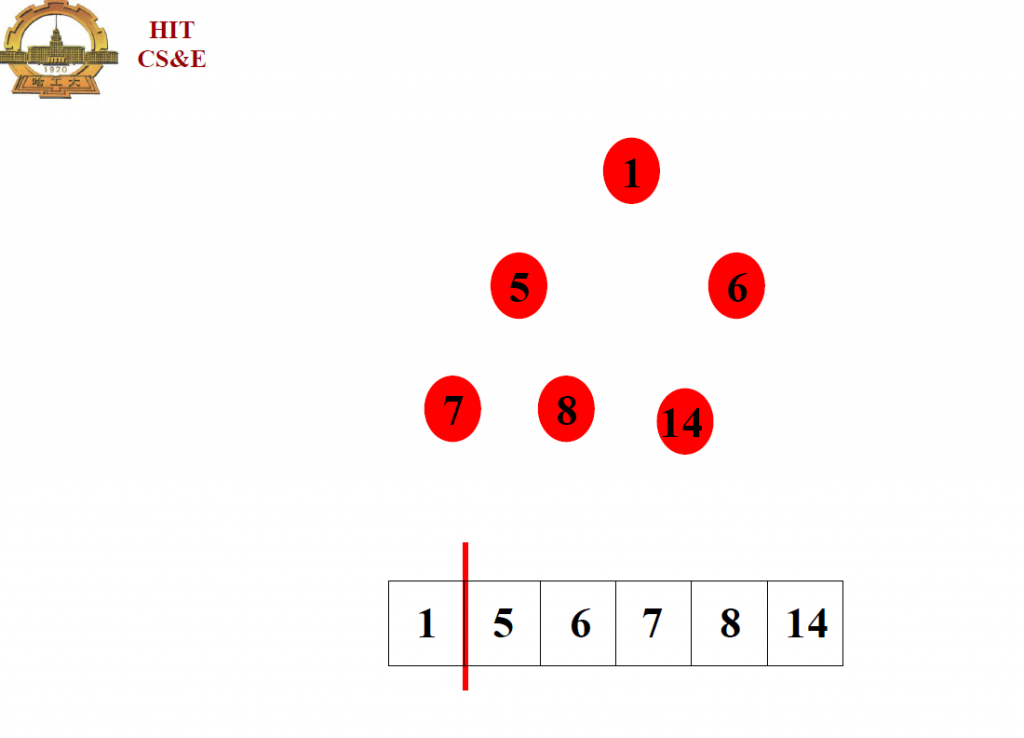
通过这个例子不难看出,主要思想是将大根堆的堆顶取出,放到数组的最后一个位置,将最后一个位置原来的数放到堆顶,然后对堆顶做调整;
7 代码实现
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <stdint.h>
4 #include <assert.h>
5 #include <string.h>
6
7 void Swap(int * array, int i, int j)
8 {
9 assert(array);
10 int tmp;
11 tmp = array[j];
12 array[j] = array[i];
13 array[i] = tmp;
14 }
15
16 /*小根堆调整*/
17 void MinHeapify(int * array, int heapSize, int currentNode)
18 {
19 int leftChild, rightChild, minimum; //左、右孩子下标;三者最小元素下标
20 leftChild = 2*currentNode + 1; //当前结点的做左孩子
21 rightChild = 2*currentNode + 2; //当前结点的做右孩子
22 if(leftChild < heapSize && array[leftChild] < array[currentNode])
23 minimum = leftChild; //有左孩子并且左孩子较小
24 else
25 minimum = currentNode;
26 if(rightChild < heapSize && array[rightChild] < array[minimum])
27 minimum = rightChild; //有右孩子并且右孩子是三者最小的
28 if(minimum != currentNode)
29 {// 当前结点不是最小的,需要交换
30 Swap(array, minimum, currentNode);
31 MinHeapify(array, heapSize, minimum); //子节点需要重新递归调整
32 }
33 }
34 /*构建小根堆*/
35 void MinHeapCreate(int * array, int heapSize)
36 {
37 int i;
38 for(i = heapSize/2; i >= 0; i--)
39 { //需要从最后一个非叶节点开始调整
40 MinHeapify(array, heapSize, i);
41 }
42 }
43
44 /*大根堆调整*/
45 void MaxHeapify(int * array, int heapSize, int currentNode)
46 {
47 int leftChild, rightChild, largest;
48 leftChild = 2*currentNode + 1;
49 rightChild = 2*currentNode + 2;
50 if(leftChild < heapSize && array[leftChild] > array[currentNode])
51 largest = leftChild;
52 else
53 largest = currentNode;
54 if(rightChild < heapSize && array[rightChild] > array[largest])
55 largest = rightChild;
56 if(largest != currentNode)
57 {
58 Swap(array, largest, currentNode);
59 MaxHeapify(array, heapSize, largest);
60 }
61 }
62
63 /*构建大根堆*/
64 void MaxHeapCreate(int * array, int heapSize)
65 { /*注意:这里只是经过一次堆调整之后,并不是将这些数完全用堆排序完成排序*/
66
67 int i;
68 for(i = heapSize/2; i >= 0; i--)
69 {
70 MaxHeapify(array, heapSize, i);
71 }
72 }
73
74 int main()
75 {
76 int tmp;
77 int array[] = {6, 1, 14, 7, 5, 8}; //源数据
78 int *res = array; /*用于输出*/
79
80 int i, heapSize = sizeof(array)/sizeof(int );
81
82 printf("Source data:\n");
83 for(i = 0; i < heapSize; i++)
84 {
85 printf("%d\t", array[i]);
86 }
87 printf("\n");
88
89 /*构建一次小根堆并输出, 每次找出最小结点*/
90 for(i = heapSize; i > 1; --i)
91 {
92 MinHeapCreate(array, i); /*一次堆调整*/
93 Swap(array, 0, i - 1); /*将最小值依次存储在数组后端*/
94 }
95
96 printf("Output the MinHeap:\n");
97 for(i = 0; i < heapSize; i++)
98 {
99 printf("%d\t", array[i]);
100 }
101 printf("\n");
102
103 /*构建大根堆并输出, 每次堆调整找出最大结点*/
104 for(i = heapSize; i > 1; --i)
105 {
106 MaxHeapCreate(array, i); /*一次堆调整*/
107 Swap(array, 0, i - 1); /*将最大值依次存储在数组后端*/
108 }
109
110 printf("Output the MaxHeap:\n");
111 for(i = 0; i < heapSize; i++)
112 {
113 printf("%d\t", array[i]);
114 }
115 return 0;
116 }
117
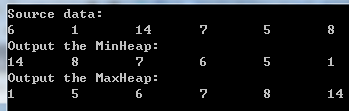
结果:使用堆排序完全排序一个数组




 浙公网安备 33010602011771号
浙公网安备 33010602011771号