支持向量机（四）----序列最小最优化算法SMO
在支持向量机（二）和（三）中，我们均遗留了一个问题未解决，即如何求解原问题的对偶问题；
在支持向量机（二）中对偶问题为：
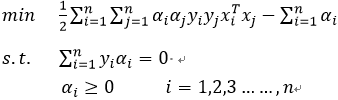
在支持向量机（三）中的对偶问题为：
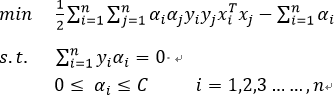
对于上述两个对偶问题，我们在支持向量机（三）中分析C的作用时有分析过，当C特别大时，松弛因子ξ=0，故此时的线性支持向量机即为线性可分支持向量机，也就是说线性可分支持向量机可以看做是线性支持向量机的一种特殊情况，故在此处，我们以支持向量机（三）中的对偶问题为例，来分析利用SMO算法求解的过程，在上述对偶问题中，变量是拉格朗日乘子，一个变量αi对应一个样本点（xi,yi）变量的总数等于样本容量n
在支持向量机（一）中我们已经讨论了原问题与对偶问题的解等价的条件，即KKT条件。SMO算法基本思路也正是KKT条件：即如果所用变量的解都需满足此最优化问题的KKT条件，那么这个最优化问题的解就得到了。也就说假如
是上述对偶问题的最优解，那么对于每一个α，均满足KKT条件，如下：（KKT条件推导见支持向量机（一））
SMO算法过程：
1.选几个变量进行优化
分析如上问题，最终我们需要优化的是n个变量α，一次型优化显然行不通，此时我们可以采用一种从局部到整体的思路，即先优化其中一部分变量，使这部分变量满足上述KKT条件，然后重复这种思路，直到n个变量α均被优化到满足KKT条件，那么此时的α即为满足条件的最优解，此时问题的关键为我们选几个变量进行优化，下边分情况讨论；
a.每次选一个变量α进行优化：
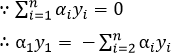
等式两边同乘以y1,即可得：
α1变化的同时等号右边也随着一起变量，显然选定一个变量和原问题没有区别
b.每次选择两个变量α进行优化：
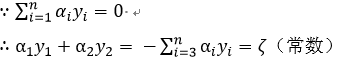
等式两边同乘以y1,可得：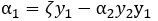
……………………………………………………………………（1）
我们可以用一个变量表示另一个变量，我们通过在优化一个变量的同时也优化了另外一个变量，这样将一个优化n个变量的问题转换成为了优化两个变量的问题，按照这样的思路，不断的重复即可优化所有的变量，使其满足KKT条件。解决了选几个的问题，接下来要解决的问题就是怎么选和如何求解的问题这才是SMO的核心，参考《李航-统计学习方法一书》，将SMO分解为两个部分：第一：求解两个变量的二次规划的解析方法；第二：选择变量的启发式方法
2.求解两个变量的二次规划的解析方法
遵循何种原则去去选择两个变量，我们在后边整理，这里我们现假定我们选α1和α2作为优化变量，我们对原式进行化简如下：
在上述化简过程中
（1）我们将和α1与α2无关的项统一表示为常数项即英文单词constant
（2）
将式（1）代入到式（2）中可得：
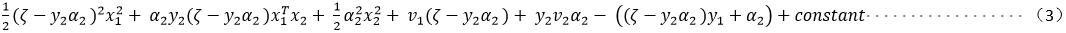
为了求解方便特令：
将（4）（5）代入（1）中得：
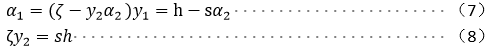
在KKT条件中：
，令
则：
则：
求解式（3）的最小值，式（3）为关于变量α2的二次函数，最值点即为极值点也就是导数为0的点，对（3）式求导并将上述（6）代入得：
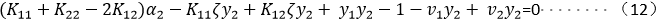
将（7）（8）（10）（11）代入（12）并化简：
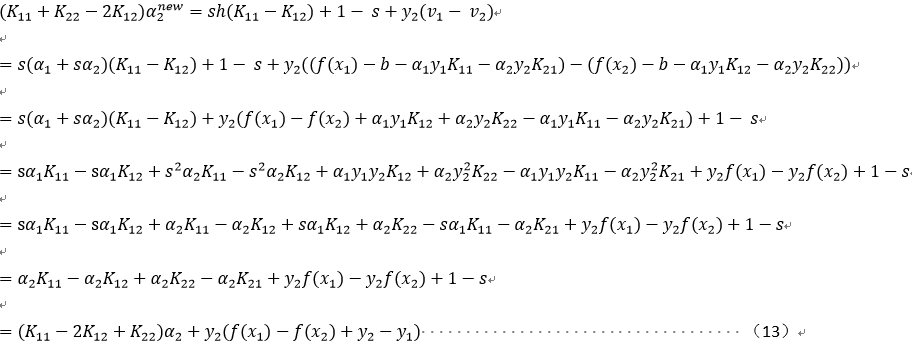
令：
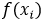为预测值，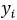
为真实值，定义
为真实值与预测值之间的误差；
则：
