LeNet – 5网络
网络结构为:
输入图像是:32x32x1的灰度图像
卷积核:5x5,stride=1
得到Conv1:28x28x6
池化层:2x2,stride=2
(池化之后再经过激活函数sigmoid)
得到Pool1:14x14x6
卷积核:5x5,stride=1
得到Conv2:10x10x16
池化层Pool2:2x2,stride=2
(池化之后再经过激活函数sigmoid)
得到Pool2:5x5x16
然后将Pool2展开,得到长度为400的向量
经过第一个全连接层,得到FC1,长度120
经过第二个全连接层,得到FC2,长度84
最后送入softmax回归,得到每个类的对应的概率值。
网络结构图如下:

LeNet大约有6万个参数
可以看出,随着网络的加深,图像的宽度和高度在缩小,与此同时,图像的通道却在不断的变大。
注:LeNet论文中的一些细节与现在的网络处理方式有些不同。阅读原始论文时,建议精读Section2,泛读Section3。不同点有以下几点:
1)论文中使用Sigmoid函数作为激活函数,而现在我们一般使用ReLU等作为激活函数;
2)现在我们使用的每个卷积核的通道数都与其上一层的通道数相同,但是LeNet受限于当时的计算机的运算速度,为了减少计算量和参数,LeNet使用了比较复杂的计算方式;
3)LeNet网络在池化层之后再进行非线性处理(即激活函数),现在的操作是经过卷积之后就经过非线性处理(激活函数),然后再进行池化操作;
AlexNet
输入图像:227x227x3的RGB图像(实际上原文中使用的图像是224x224x3,推导的时候使用227x227x3会好一点)
Filter1:11x11,stride=4
得到Conv1:55x55x96
Max-POOL1:3x3,stride=2
得到Conv2:27x27x96
Filter2: 5x5,padding=same
得到Conv3: 27x27x256
Max-Pool2: 3x3,stride=2
得到Conv4: 13x13x256
Filter3: 3x3,padding=same
得到Conv5: 13x13x384
Filter4: 3x3,padding=same
得到Conv6: 13x13x384
Filter5: 3x3,padding=same
得到Conv6: 13x13x256
Max-Pool3: 3x3,stride=2
得到Conv7: 6x6x256
然后将Conv7展开,得到一个长度为6x6x256=9216的向量
经过第一个全连接层
得到FC1: 4096
经过第二个全连接层
得到FC2: 4096
最后使用softmax函数输出识别的结果
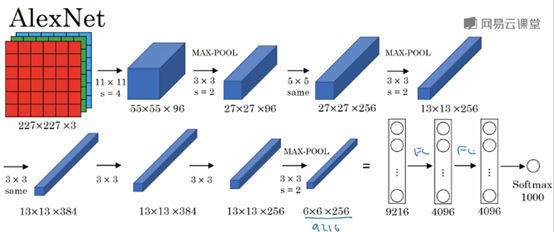
AlexNet包含大约6000万个参数。
AlexNet使用了ReLU激活函数;
AlexNet也使用了LRN层(Local Response Normalization,局部响应归一化层),但是由于LRN可能作用并不大,应用的比较少,在此不再详述。
VGG-16
VGG16网络包含了16个卷积层和全连接层。
VGG网络的一大优点是:简化了神经网络结构。
VGG网络使用的统一的卷积核大小:3x3,stride=1,padding=same,统一的Max-Pool: 2x2,stride=2。
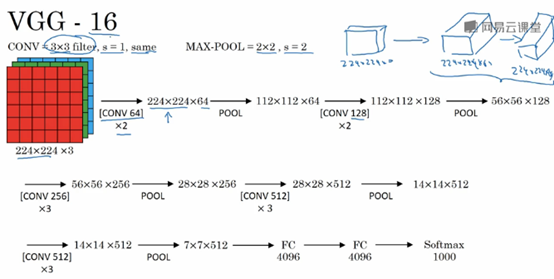
VGG16是一个很大的网络,总共包含1.38亿个参数。因此其主要缺点就是需要训练的特征数量非常巨大。
另外也有VGG19网络,由于VGG16表现几乎和VGG16不分高下,所以很多人还是会使用VGG16。
残差网络(Residual Networks,ResNet)
因为存在梯度消失和梯度爆炸(vanishing and exploding gradients),非常深的网络是很难训练的。
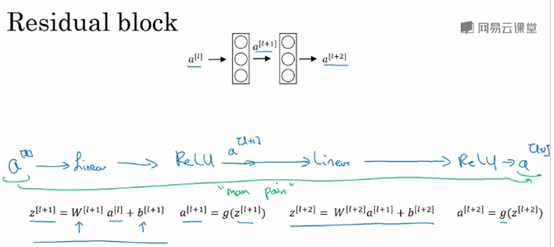
ResNet由残差块(Residual block)组成,
信息流从a[l]到a[l+2],普通的网络需要经过以下几个步骤,称为主路径。
Shortcut/skip connection指a[l]跳过一层或者好几层,从而将信息传递到神经网络的更深层。
Shortcut/skip connection在进行ReLU非线性激活之前加上,如下图所示:
如果我们使用标准的优化算法训练一个普通网络,凭经验,你会发现随着网络深度的加深,训练错误会先减少,然后增多。而理论上,随着网络深度的加深,应该训练的越来越好才对,但是实际上,如果没有残差网络,对于一个普通的网络来说,深度越深意味着用优化算法越难训练。但是有了ResNet就不一样了,即使网络再深,训练的表现却不错,比如说错误会减少,就算训练深度达到100层的网络也不例外。 这种方式确实有助于解决梯度消失和梯度爆炸问题,让我们在训练更深网络的同时,又能保证良好的性能。
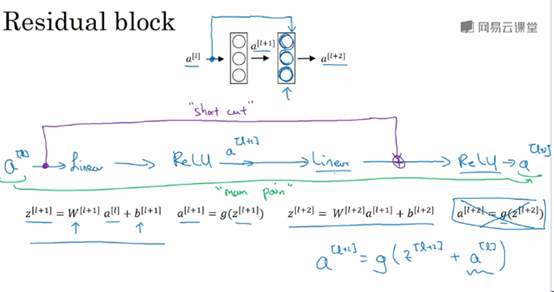
注:上图中,Plain network指的是没有加上蓝色单箭头线的网络;ResNet指的是画上蓝色箭头线的网络。
为什么ResNet能有如此好的表现?
上面讲到,一个网络越深,它在训练集上训练网络的效率会有所减弱,这也是有时候我们不希望加深网络的原因,但是ResNet却能克服这个问题。
假设有一个大型的神经网络,其输入为X,输出激活值a[l],如果你想增加这个神经网络的深度,比如下图,在原网络后面再加上两层全连接层,得到新的激活函数a[l+2]。
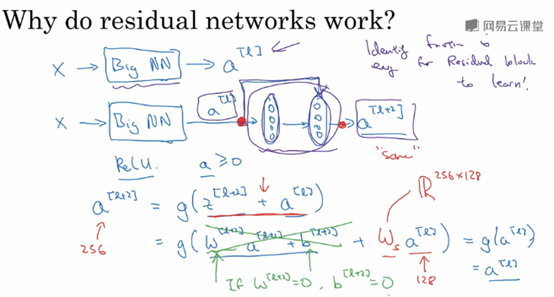
Shortcut使得我们很容易得出a[l+2]=a[l],这意味着即使给神经网络增加了这两层,它的效率也并不逊色于更简单的神经网络。因为只要使得新添加的两层的权重和偏置为0,那么新网络就跟原始网络效果是一样的。但是如果新添加的这些隐层单元学到一些有用信息,那么它可能比学习恒等函数表现更好。
具体可以看这篇文章:http://www.cnblogs.com/hejunlin1992/p/7751516.html
假设z[l+2]与a[l]具有相同维度,所以ResNet使用了许多相同卷积
如果输入与输出有不同的维度,比如说输入的维度是128,a[l]的维度是256,再增加一个矩阵Ws,Ws是一个256x128维度的矩阵,所以Ws乘以a[l]的维度是256,你不需要对Ws做任何操作,它是通过学习得到的矩阵或参数,它是一个固定的矩阵,padding的值为0
内容主要来自与:
Andrew Ng的卷积神经网络课程

