使用最大似然法来求解线性模型（3）-求解似然函数

根据 使用最大似然法来求解线性模型（2）-为什么是最大化似然函数？ 中提到，某个随机变量t_n的 条件概率 服从均值为w^T*x_n，方差为σ²的正态分布。

 

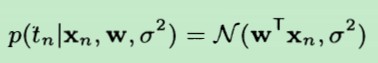
现在假设有N个样本点，它们的联合概率密度为：

 

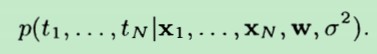
由于在给定了w和σ²的条件下，t_n之间是相互独立的。即：在给定的 w，σ²的条件下，t₁ t₂ ...t_n 之间是相互独立的（这就是朴素贝叶斯假设！）

故联合概率密度可写成下式：

 

为什么 t_n在给定了w和σ²的条件下是相互独立的呢？如果直接从图形上看，不是相互独立的，各个t_n之间大致是一个单调的线性下降关系。也即：t₁<t₂<...<t_n

这个单调下降的线性关系就是由 w 决定的(体现的)。

在给定了w的条件下，每年的奥林匹克男子100m时间的年份之间就没有必然的联系了，就好像16年奥运会男子100m的时间 与 06 年奥林匹克男子100m的时间 是没有关系，相互独立的。

但从整个历史趋势(1960-2020)来看，奥林匹克男子100m所花的时间是越来越少的。

 

这里需要注意的是：t是条件独立的，即在给定的w条件下，各个t之间是相互独立的。上面的 L 就是似然函数。

要想最大化L，相当于最大化logL，于是就有：

 

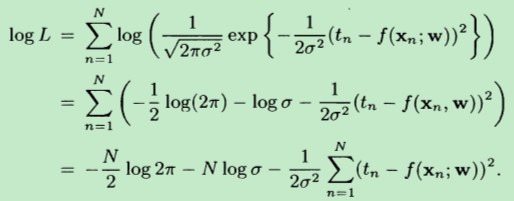
其中，f(x;w)=w*x，代入上式，得到：

 

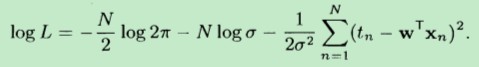
让logL 对 w 求偏(将x_n 、t_n 和 δ 都视为常数)，并令偏导数等于0，根据向量乘法：w^T*x_n = x_n^T * w。故得到：

 

需要注意的是：上式X_n是一个向量，X_nT=[1,x_n]，表示的是年份，即哪一年的比赛数据，比如x₁₀=1980。前面的1 是偏置项。

因为：w^T*x_n=w₀*1+w₁*x_n.  w^T=(w₀,w₁)有两个参数，故需要一个bias unit(偏置项)

为什么w有两个参数(w₀,w₁)呢？因为我们是用直线来拟合数据。根据直线的一般表达式方程 y=k*x+b，需要两个参数，一个是斜率k，另一个是截距b

只要给定了斜率和截距，就能唯一确定一条直线了。而对于向量w，分量w₀相当于截距，分量w₁相当于斜率。

 

t_n是一个标量，表示的是第n个样本点代表的年份，比如t₁₀=10.25 表示第10个样本点所表示的奥林匹克男子100m所花的时间是10.25秒。

w是一个向量，即线性模型里面的模型参数。它们的具体形式如下(n 和 N 没有区别)：

 

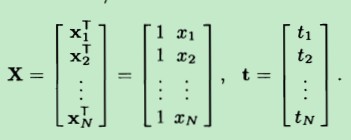
把求和累加化简，根据矩阵乘法：(注意下面x一个是向量，一个是单个实数x。它们之间的关系：X_nT=[1,x_n])

 

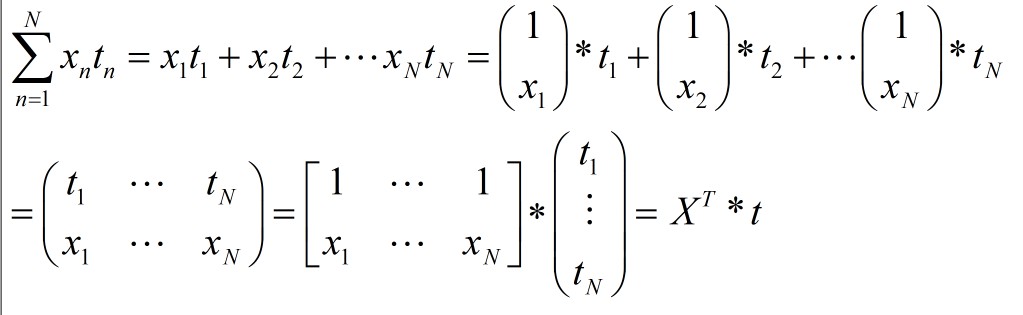
这样，我们就可以将偏导数表示成，更紧凑的矩阵乘法的形式，如下：

 

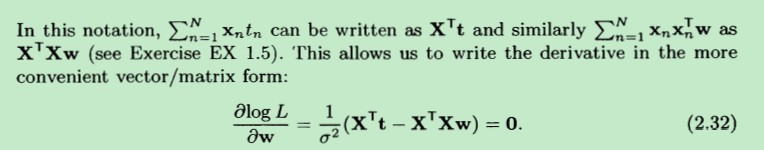
并最终求得w，结果用w^Λ 来表示：

 

根据模型的概率密度函数：

 

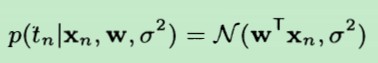
还需要求解σ²。同样地，logL对σ求偏导数，并令偏导数等于0，得到下面公式：

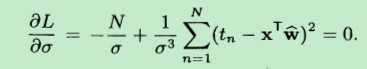（图中应该是 logL 而不是L）

 

最终解得为σ²：

 

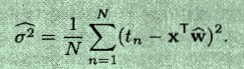
将求得的w^Λ 代入到上式（具体推导见参考文献），得到：

 

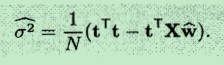
根据上面求解的w和δ² 的公式，现在只要给定若干个数据(训练样本X)，就可以计算出w和δ² ，从而求出了：

 

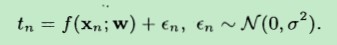
知道了概率密度表达式中所有的参数：w和δ² ，当然也就求得了概率密度：

 

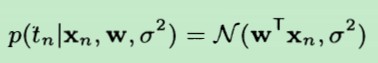
最终得出带有 ξ_n的能够估计 noise的“线性”模型。因为，此时我们的模型估计值t_n是一个 随机变量了，随机变量的variance（各个点取值的偏差由δ² 决定）。

 

参考文献：《A First Course of Machine Learning》

原文：http://www.cnblogs.com/hapjin/p/6623795.html