使用最大似然法来求解线性模型（2）-为什么是最大化似然函数？

根据 使用最大似然法来求解线性模型（1），待求解的线性模型如下式：

• t_n=w^T*x_n+ξ_n

第x_n年的百米赛跑的时间t_n，与两个参数有关：一个是w，另一个则是该年对应的一个误差值(noise)

在求解w和 ξ 之前，先观察一下误差值的特点：

 

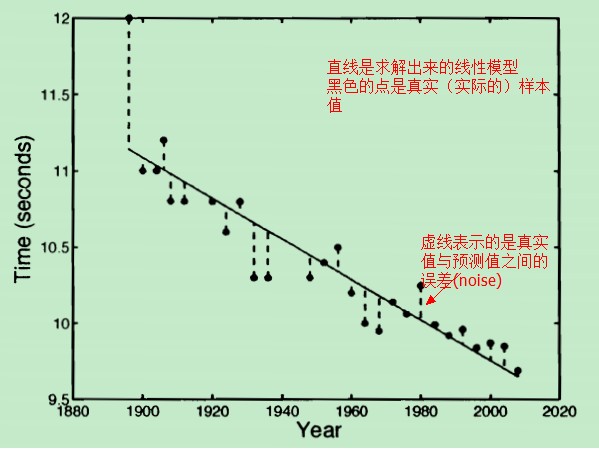
1. 误差有正有负，是一个随机变量。
2. 误差与年份无关，每一个年份对应的误差之间相互独立

 

因此，关于errors（noise）的假设如下：

 

更进一步，假设errors(noise)服从高斯分布，模型表示如下：显然这个模型由两个参数来决定：w 和 σ²，只要确定这两个参数，就确定了这个模型。

 

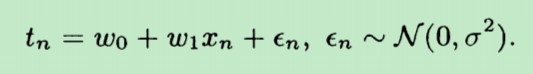
这N个误差的联合概率密度为：p(ξ₁，ξ₂，...，ξ_N)，由于它们相互独立，故有：

 

 

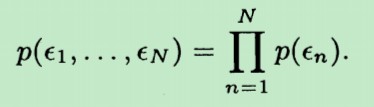
现在，t_n 表示成了一个常数(w₀+w₁*x_n) 加上 一个服从高斯分布的随机变量ξ_n，故t_n 也相当于一个服从正态分布的随机变量了。根据正态分布性质：

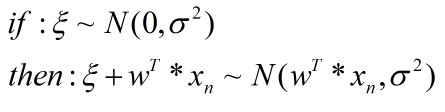
得出：

 

那t_n为什么是个条件概率呢？

根据上面t_n的表达式，在给定的w和ξ_n之后，我们就知道了t_n。而ξ_n服从正态分布，由σ²来确定。故t_n可表示成如上的条件概率形式。

 

现在不妨假设已经求得了w=[36.416,-0.0133]^T和σ²=0.05，在x_n=1980年时，上面的条件概率公式表示如下：

 

随机变量的均值由w^T*x_n计算得到，均值u=10.02，而方差是0.05

 

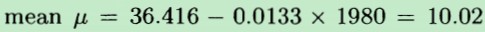
故它的概率密度函数如下：

 

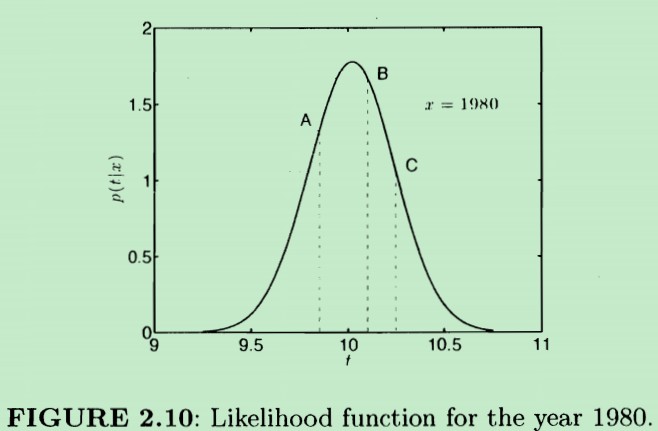
在概率密度函数中有三个点A，B，C。其中B点对应的时间t约是t_B=10.1，C点对应的时间t是t_C=10.25

从图中可以看出：在A，B，C三个点中，B点对应的概率密度最大(y轴的值最高)，根据正态分布的概率密度性质，说明随机变量取B点处的值的概率最大，也即：随机变量t_n最可能的取值是10.1秒

但是，我们实际观察到的1980年奥林匹克竞赛男子100m赛跑的时间是：10.25秒，这是实际的样本值，也即上面概率密度函数中C点对应的值。

因此，问题就来了：

我们需要修改(重新求解)w和的σ²值(原来的值为：w=[36.416,-0.0133]^T  σ²=0.05)，使得：根据w和σ²画出的概率密度函数在t=10.25处最高，也即在t=10.25处取值的概率最大。

换句话说：我们需要寻找合适的w和σ²，让模型的概率密度函数在 实际值10.25秒 时，对应的概率密度最大。

我们把实际的样本值t=10.25 称为样本点x_n=1980 所对应的 似然值(likelihood of data point 1980)。

目标是：寻找合适的w和σ² 让概率密度函数在真实值10.25秒 时对应的概率密度最大。而这就是最大化似然函数的思想。

 

参考：《A First Course of Machine Learning》第二章

 

原文：http://www.cnblogs.com/hapjin/p/6623431.html