深度学习7softmax回归
softmax回归可以解决两种以上的分类,该模型是logistic回归模型在分类问题上的推广。
对于y可以取两个以上的值,比如说判断一份邮件是垃圾邮件、个人邮件还是工作邮件。
这边也参考http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
也就是对于给定的输入x,我们想用假设函数针对每一个类别j估算p(y=j|x),也就是估算出每一种分类结果出现的概率。对于logistic回归中,y取0跟1,我们采用假设函数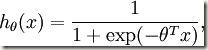 我们将训练模型参数
我们将训练模型参数 ![]() ,使其能够最小化代价函数 :
,使其能够最小化代价函数 :
就是这边为什么乘以-1/m
而在softmax回归中,y取多个值k,因此,我们的假设函数将要输出一个 ![]() 维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这 ![]() 个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 ![]() 形式如下:
形式如下:
下面就看看这个是怎么来的。
首先定义每个结果的概率,
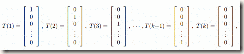
则,这个问题我们可以看成事k-1维的问题。则这个时候的T(y)就不是y,而是一组k-1维的向量,也就是T(y)要给出每一个y=i的概率(i从1到k-1)对于这个问题也演化到一般线性模型上面,即
将这多个向量也转化到指数分布上。下面定义:
好,下面我们的目的也就是使得每个![]() 在其i时的概率最大,转化到一般线性模型下,即
在其i时的概率最大,转化到一般线性模型下,即
则:
从η到φ我们就叫做softmax回归。
这样我们就得到了上面的假设函数,换个写法
下面再反过来求最大似然估计
最后我们再用牛顿法或者梯度下降法解出θ
整个过程有了,但是还没有能够进行深入理解,对于更多细节参考
http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
下面做一下这个后面的练习来加深理解。




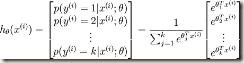
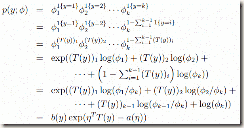
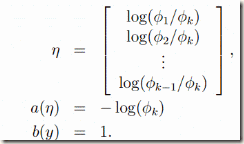
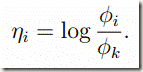
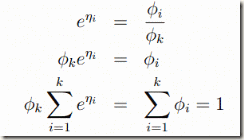


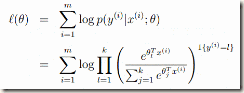

 浙公网安备 33010602011771号
浙公网安备 33010602011771号