【组合数学】 04 - 基本计数问题

1. 基本计数

1.1 统一模型

　　本篇来讨论几个基本的计数问题，这些问题虽然都有各自的模型，但本质上却有着内在的联系，因此我们先建立一个统一的模型。现在有元素集\(E,F\)，它们的元素都有内在的结构，建立映射\(E\to F\)，问题是这样的映射有多少个？满射和单射有多少个？

　　所谓有内在的结构，就是元素间的拓扑结构，我们所说的映射个数，严格讲是在拓扑同构意义下的等价类的个数。拓扑结构种类繁多，无法一一研究，本篇只探讨两个基本的拓扑结构，下一篇会做更一般性的讨论。这个模型虽然对本章作用有限，但可以从更高的视角思考看待问题的本质，而且各个问题间联系也一目了然。

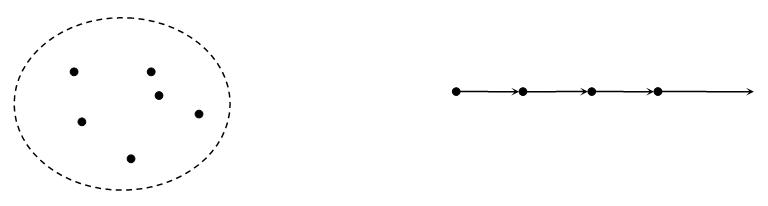
　　两个基本拓扑结构分别是：无序结构和有向链表。无序结构中的元素是离散的、无差别的，在拓扑同构下可以互相替换。有向链表中的元素是完全区分的，它的拓扑同构只有自身，当然只有自身的拓扑结构不止这一个，这里只要强调完全区分性，所谓有向链表可以当做是给每个元素编了号。以下设\(E,F\)都是有限集，且记\(|E|=m,|F|=n\)。

1.2 模型1：可区分\(\to\)可区分

　　可完全区分的结构比较简单，先来看\(E,F\)都是有向链表的情况，\(E,F\)分别纵向排列，\(E\to F\)就是一般的函数定义。对\(E\)的每个元素都有\(n\)个值可以映射，由乘法原理便知映射一共有\(n^m\)种。这个结构有一个更常用、更直观的模型，考察由\(n\)个字母组成的集合\(S\)，用这些字母组成长度为\(m\)的单词\(x_1x_2\cdots x_m\)。这个单词也被称\(S\)上的\(m\)元可重复排列，或\(m\)元字。不难证明它和模型1的等价性，故\(S\)上的\(m\)元字有\(n^m\)个。

　　现在对映射添加一些限制，比如假设\(E\)的第\(k\)个元只能取某\(n_k\)个值，由乘法定理知可以有\(n_1n_2\cdots n_m\)个\(m\)元字。再限制每个元素的映射不能相同，或者说字中没有重复字母，第\(k\)个元素只能取\(n-k+1\)个值。这其实就是我们熟悉的\(n\)个元素中选\(m\)个元素的排列数\(P(n,m)\)（式（1）），其中表达式\(x(x-1)\cdots(x-k+1)\)简记为\((x)_k\)，也叫做\(x\)的降\(k\)阶乘（\(x\)不要求是自然数）。类似地记表达式\(x(x+1)\cdots(x+k-1)\)简记为\((x)^k\)，也叫做\(x\)的升\(k\)阶乘。

\[P(n,m)=(n)_m=n(n-1)\cdots(n-m+1)=\dfrac{n!}{(n-m)!}\tag{1}\]

　　排列数要求每个函数值最多被映射一次，继续推广，我们假定\(F\)中第\(k\)个数被映射\(m_k\)次。这样的字称为是\(a_1^{m_1}a_2^{m_2}\cdots a_n^{m_n}\)型字，其中\(m_1+m_2+\cdots+m_n=m\)。先将\(m_k\)个字母\(a_k\)看成互异的字母\(a_{k1},\cdots,a_{km_k}\)，这样的字有\(m!\)个，而原来的每个字对应到\(m_1!m_2!\cdots m_n!\)个这样的字，故有式（2）成立。

\[N(a_1^{m_1}a_2^{m_2}\cdots a_n^{m_n})=\dfrac{m!}{m_1!m_2!\cdots m_n!}\tag{2}\]

　　• 求\(S\)上的相邻字母不相同的\(m\)元字的个数。

1.3 模型2：不可区分\(\to\)可区分

　　现在假定\(E\)是无序的，而\(F\)是有向链表，由于原像不可区分，要关注的便是像的组合情况。它的一个等价模型我们也很熟悉：从\(n\)种颜色的球里选出\(m\)个球。如果要求每种颜色只能选一个，相当于映射为单射，选取个数称为\(n\)的\(m\)元不重复组合数，记作\(\binom{n}{m}\)，一般也简称为组合数。它其实就是排列在\(E\)无序下的等价类的个数，具体说就是\(m!\)个排列属于同一个等价类，故有公式（3）。

\[\binom{n}{m}=\dfrac{(n)_m}{m!}=\dfrac{n!}{m!(n-m)!}\tag{3}\]

　　如果颜色可以重复选，选取个数称为\(n\)的\(m\)元可重复组合数，记作\(\left(\binom{n}{m}\right)\)。设每个像被映射的次数为\(x_k\)，可重复组合数等价于方程（4）的非负整数解的个数。对这个问题，有两个比较巧妙的方法，它们都把可重复组合问题转化为了不重复组合问题，其中的对应思想是非常重要的。一种方法是直接理解方程（4），它相当于把\(m\)个相同的元素分割为可区分的\(n\)份。将\(m\)个元素一字排开，在其中插入\(n-1\)个隔板即可，隔板和元素共\(m+n-1\)个位子，我们就是要选择其中的\(n-1\)个位置，这就有式（5）成立。

\[x_1+x_2+\cdots+x_n=m\tag{4}\]

\[\left(\binom{n}{m}\right)=\binom{m+n-1}{m}=\dfrac{(n)^m}{m!}\tag{5}\]

　　另一种解释式（4）的方法也非常经典，考察\(s_k=x_1+\cdots+x_k\)组成的单调递增序列（式（6）左），\(s_k\)在\([n]\)中取值，但可能存在重复值。为了消除等号，再令\(t_k=s_k+k-1\)，这时有式（6）成立，其中\(t_k\)在\([m+n-1]\)中取互异值，同样得到公式（5）。利用这个思想，更容易得到不等式（7）的非负整数解为\(\binom{m+n}{m}\)，它也相当于左式分别取\(0\sim m\)时的解数和，故有式（8）成立。

\[0\leqslant s_1\leqslant\cdots\leqslant s_n=m\;\Leftrightarrow\;0\leqslant t_1<\cdots<t_n=m+n-1,\;t_k=s_k+k-1\tag{6}\]

\[x_1+x_2+\cdots+x_n\leqslant m\tag{7}\]

\[\sum_{k=0}^m\binom{n+k-1}{k}=\binom{n+m}{m}\tag{8}\]

　　• \([n]\)中取\(m\)个互不相邻的数，求取法个数。

1.4 模型3：可区分\(\to\)不可区分

　　像不可区分，就好比\(n\)个相同的篮子，把可区分的原像看做是\(m\)个不同的球，问题等价于：\(m\)个不同的球放进\(n\)个篮子的方法。根据有球的篮子数\(k\)，问题被分为\(n\)种情况，每一种情况都是相同的问题：\(m\)个球分成\(k\)堆的分法。我们就集中研究这个问题，而\(m\)个元素分成\(k\)部分的个数被称为第二类Stirling数，记作\(S(m,k)\)。

　　Stirling数并没有简单的表达式，我们先从它的递推关系入手，这也是组数计算问题的常用方法。考察某个元素\(a_1\)，分割后有两种情况：它单独分为一堆，或和其它元素在一堆。所以很容易有递推关系（9）。使用递推关系归纳，可以得到比较漂亮的公式（10），如果你觉得正向证明不明显，可以试试反向证明。

\[S(m,k)=S(m-1,k-1)+kS(m-1,k)\tag{9}\]

\[S(k+r,k)=\sum_{1\leqslant k_1\leqslant k_2\leqslant\cdots\leqslant k_r\leqslant k}k_1k_2\cdots k_r\tag{10}\]

　　考虑模型3和模型1的关系，模型3中的1个分割是模型1中的一个等价类：被映射的像的个数为\(k\)。这个等价类中有\(\binom{n}{k}k!=(n)_k\)个元素（先选\(k\)个像再排列），从而我们有重要的关系式（11）（\(S(m,0)=0\)）。\(m\)个元素的总分割数被称为Bell数，记作\(B_m\)，它显然是式（12）左。以某个元素所在堆的大小分类讨论，容易有递推关系式（12）右。

\[n^m=\sum_{k=0}^nS(m,k)(n)_k\tag{11}\]

\[B_m=\sum_{k=0}^mS(m,k)\;\Rightarrow\;B_{m+1}=\sum_{k=0}^m\binom{m}{k}B_{m-k}\tag{12}\]

1.5 模型4：不可区分\(\to\)不可区分

　　当原像和像都不可区分时，只需关心分割的堆数和每堆的个数，等价的模型就是整数\(m\)的分拆数\(p(n)\)。对应地分拆为\(k\)部分的个数记作\(p(m,k)\)，它表示不定方程（13）正整数解的个数，注意它和方程（4）的区别在于不考虑分拆的顺序。既然不考虑各部分的顺序，每个分拆其实还对应方程（14）的一组非负整数解。

\[x_1+x_2+\cdots+x_k=m,\;\;(x_1\geqslant x_2\geqslant\cdots\geqslant x_k)\tag{13}\]

\[x_1+2x_2+3x_3+\cdots+mx_m=m\tag{14}\]

　　分拆数同样没有简单的表达式，我们还是先来建立一些递推关系式。根据\(x_k\)是否为\(1\)可得到递推关系（15），持续使用该式便得到式（16），它也有显然的组合意义。

\[p(m,k)=p(m-1,k-1)+p(m-k,k)\tag{15}\]

\[p(k+r,k)=p(r,1)+p(r,2)+\cdots+p(r,k)\tag{16}\]

　　关于\(m\)的某个分拆结果\(x_1,x_2,\cdots,x_k\)，有个直观的表示方法，以点表示不可区分的元素，在第\(i\)行排列\(x_i\)个点。比如\((5,5,3,2)\)画成下图，这样的图称为菲勒（Ferrers）示意图，利用其直观性可以得到很多意想不到的结论。菲勒图纵横翻转后仍然是菲勒图，它对应的分拆称为原分拆的共轭分拆，对于分拆\(\pi\)，其共轭分拆一般记作\(\pi^*\)。从菲勒图中容易得到：（1）\(p(m,k)\)等于\(m\)最大分部为\(k\)的分拆数；（2）\(m\)最多\(k\)个部分的分拆数，等于\(m\)最大分部不大于\(k\)的分拆数。

　　满足\(\pi=\pi^*\)的分拆称为自共轭分拆，它的菲勒图沿对角线对称。将其菲勒图按如图所示分割，便知\(m\)的自共轭分拆数等于各部分是不同奇数的分拆数。再看各部分都不同的分拆，每个部分\(x_k\)都可以唯一地表示为\(i\cdot 2^j\)，其中\(i\)为奇数。把该部分拆分为\(2^j\)个\(i\)，最终得到所有部分为奇数的分拆。反之对各部分为奇数的分拆，因为大小为\(i\)的部分的个数可以唯一表示为\(2\)的幂次之和，故这个对应关系是双向的。这就是说，各部分不相等的分拆数等于各部分为奇数的分拆数。

2. 基本计数的性质

2.1 二项式系数

　　前面我们已经讨论过，组合数\(\binom{n}{m}\)是\((1+x)^n\)展开式中\(x^m\)项的系数，当然也二项式（17）中\(x^my^{n-m}\)项的系数，故它也称为二项式系数。组合数的定义式（3）中，\(\dfrac{n!}{m!(n-m)!}\)要求\(m,n\)都是非负整数，但\(\dfrac{(n)_m}{m!}\)中\(n\)可以为任何实数，以后形式\(\binom{x}{m}\)也可以用来表示多项式\(\dfrac{(x)_m}{m!}\)。这个推广其实是合理的，而在微积分中我们知道\((1+x)^{\alpha}\)的幂级数展开式如式（18）所示（牛顿二项式定理），它正是\((1+x)^n\)的推广。另外易知，可重复组合数还可以写成式（19）。

\[(x+y)^n=\sum_{k=0}^n\binom{n}{k}x^ky^{n-k}\tag{17}\]

\[(1+x)^{\alpha}=1+\sum_{k=1}^{\infty}\binom{\alpha}{k}x^k\tag{18}\]

\[\left(\binom{n}{m}\right)=(-1)^m\binom{-n}{m}\tag{19}\]

　　在中学我们就知道一些二项式系数的性质，证明都不难，这里仅仅列举。式（20）中分别是对称性和递推性，其中递推性有显然的组合意义。式（21）是随\(m\)的变化体现出来的单峰性。\((1+x)^n\)中令\(x=\pm 1\)可得式（22）和（23），另外利用\((1+x)^m(1+x)^n=(1+x)^{m+n}\)可得范德蒙恒等式（Vandermonde）（24）。

\[\binom{n}{m}=\binom{n}{n-m};\;\;\binom{n}{m}=\binom{n-1}{m-1}+\binom{n-1}{m}\tag{20}\]

\[\binom{n}{0}<\binom{n}{1}<\cdots<\binom{n}{\lfloor\frac{n}{2}\rfloor}=\binom{n}{\lceil\frac{n}{2}\rceil}>\cdots>\binom{n}{n}\tag{21}\]

\[\binom{n}{0}+\binom{n}{1}+\cdots+\binom{n}{n}=2^n\tag{22}\]

\[\binom{n}{0}+\binom{n}{2}+\binom{n}{4}+\cdots=\binom{n}{1}+\binom{n}{3}+\binom{n}{5}+\cdots=2^{n-1}\tag{23}\]

\[\sum_{k=0}^r\binom{m}{k}\binom{n}{r-k}=\binom{m+n}{r}\tag{24}\]

　　二项式系数很早就被研究，最著名的当然就是杨辉三角（帕斯卡三角），它正是利用了公式（20）右。在反演公式那一章我们已经知道，矩阵\(\{a_{ij}=\binom{i}{j}\}\)的逆矩阵是\(\{b_{ij}=(-1)^{i-j}\binom{i}{j}\}\)，故有式（25）成立，当然你也可以直接证明它。

\[\sum_{k=0}^n(-1)^{k+m}\binom{n}{k}\binom{k}{m}=\delta_{mn}=\left\{\begin{matrix}1,&\text{if}\;m=n\\0,&\text{if}\;m\ne n\end{matrix}\right.\tag{25}\]

　　• 证明：\(\sum\limits_{k=0}^n\binom{n}{k}^2=\binom{2n}{n}\)；

　　• 证明：\(\binom{n}{1}+2\binom{n}{2}+\cdots+n\binom{n}{n}=n\cdot 2^{n-1}\)；

　　• 写出\((x_1+x_2+\cdots+x_p)^n\)的展开式。

2.2 Stirling数

　　现在继续讨论第二类Stirling数，从名字就知道它是个有故事的数。公式（10）并不能让人满意，它甚至只是另一个计数问题的描述而已，能使用的就只有公式（11）了。该式显然满足单链\(L_m\)的反演公式的形式，把它整理为式（25）左式（为了得到关联函数\(\binom{n}{k}\)），由反演公式得到了式（25）右，从而有\(S(n,k)\)的另一个显式表达式（26）。

\[n^m=\sum_{k=0}^n\binom{n}{k}k!S(m,k)\;\Leftrightarrow\;n!S(m,n)=\sum_{k=0}^n(-1)^{n-k}\binom{n}{k}k^m\tag{25}\]

\[S(m,k)=\dfrac{1}{k!}\sum_{i=0}^k(-1)^{k-i}\binom{k}{i}k^m\tag{26}\]

　　由于公式（11）对任意\(n\leqslant m\)成立，故有等式（27）左成立，从而\(S(m,k)\)给出了多项式组\(\{x^m\}\)和\(\{(x)_m\}\)的线性表出关系。这样的线性表出必定有逆关系（式（27）右），其中的\(s(m,k)\)就被称为第一类Stirling数，它和第一类Stirling数有关系式（28）。

\[x^m=\sum_{k=0}^mS(m,k)(x)_k\;\Leftrightarrow\;(x)_m=\sum_{k=0}^ms(m,k)x^k\tag{27}\]

\[\sum_{k=0}^mS(m,k)s(k,n)=\delta_{nm}=\left\{\begin{matrix}1,&\text{if}\;m=n\\0,&\text{if}\;m\ne n\end{matrix}\right.\tag{28}\]

　　另一方面，考察式（27）右，不难知道\(s(m,k)\)有递推式（29），类似地有表达式（30）。\(s(m,k)\)正负项交叉出现，为了寻找其组合意义，考察表达式（31）中的\(c(m,k)\)。它显然是\(s(m,k)\)的绝对值，并且满足式（32）。容易验证，含有\(k\)个轮换的\(m\)元置换数，也满足式（32）的递推关系，这便是它的组合意义。

\[s(m,k)=s(m-1,k-1)-(m-1)s(m-1,k)\tag{29}\]

\[s(k+r,k)=(-1)^r\sum_{1\leqslant k_1\leqslant k_2\leqslant\cdots\leqslant k_r\leqslant k+r}k_1k_2\cdots k_r\tag{30}\]

\[(x)^m=\sum\limits_{k=0}^mc(m,k)x^k\tag{31}\]

\[c(m,k)=c(m-1,k-1)+(m-1)c(m-1,k)\tag{32}\]

　　• 求\(1^{\lambda_1}2^{\lambda_2}\cdots m^{\lambda_m}\)型置换的个数。