wand(weak and)算法基本思路

　　一般搜索的query比较短，但如果query比较长，如是一段文本，需要搜索相似的文本，这时候一般就需要wand算法，该算法在广告系统中有比较成熟的应该，主要是adsense场景，需要搜索一个页面内容的相似广告。

　　Wand方法简单来说，一般我们在计算文本相关性的时候，会通过倒排索引的方式进行查询，通过倒排索引已经要比全量遍历节约大量时间，但是有时候仍然很慢。
　　原因是很多时候我们其实只是想要top n个结果，一些结果明显较差的也进行了复杂的相关性计算，而weak-and算法通过计算每个词的贡献上限来估计文档的相关性上限，从而建立一个阈值对倒排中的结果进行减枝，从而得到提速的效果。

　　wand算法首先要估计每个词对相关性贡献的上限，最简单的相关性就是TF*IDF，一般query中词的TF均为1，IDF是固定的，因此就是估计一个词在文档中的词频TF上限，一般TF需要归一化，即除以文档所有词的个数，因此，就是要估算一个词在文档中所能占到的最大比例，这个线下计算即可。

　　知道了一个词的相关性上界值，就可以知道一个query和一个文档的相关性上限值，显然就是他们共同的词的相关性上限值的和。

　　这样对于一个query，获得其所有词的相关性贡献上限，然后对一个文档，看其和query中都出现的词，然后求这些词的贡献和即可，然后和一个预设值比较，如果超过预设值，则进入下一步的计算，否则则丢弃。

　　如果按照这样的方法计算n个最相似文档，就要取出所有的文档，每个文档作预计算，比较threshold，然后决定是否在top-n之列。这样计算当然可行，但是还是可以优化的。优化的出发点就是尽量减少预计算，wand论文中提到的算法如下：

　　其基本思路是基于倒排索引来实现WAND方法：

　　首先是初始化：

1. 提取出da中所有的词，以及这些词的倒排索引；
2. 初始化curDoc=0；
3. 初始化posting数组，使得posting[t]为词t倒排索引中第一个文档；

　　然后是寻找下一个需要完全计算权值的问题，具体流程如下：

可以定义一个next函数，用于查找下一个进行完全计算的文档，论文中对next描述如下：

Function next(θ) repeat /* Sort the terms in non decreasing order of DID */ sort(terms, posting) /* Find pivot term - the first one with accumulated UB ≥ θ */ pTerm ← findPivotTerm(terms, θ) if (pTerm = null) return (NoMoreDocs) pivot ← posting[pTerm].DID if (pivot = lastID) return (NoMoreDocs) if (pivot ≤ curDoc) /* pivot has already been considered, advance one of the preceding terms */ aterm ← pickTerm(terms[0..pTerm]) posting[aterm] ← aterm.iterator.next(curDoc+1) else /* pivot > curDoc */ if (posting[0].DID = pivot) //注，这个是sort之后的第一个term位置的doc id /* Success, all terms preceding pTerm belong to the pivot */ curDoc ← pivot return (curDoc, posting) else /* not enough mass yet on pivot, advance one of the preceding terms */ aterm ← pickTerm(terms[0..pTerm]) posting[aterm] ← aterm.iterator.next(pivot) end repeat

其中用到了几个函数，解释如下：

aterm.iterator.next(n)

这个函数返回aterm倒排索引中的DID，这个DID要满足DID >= n。DID就是docID

sort(terms, posting)

sort是把terms按照posting当前指向的DID的非递减排序。比如da所有词的倒排索引为：

• t0: [1, 3, 26]
• t1: [1, 2, 4, 10, 100]
• t2: [2, 3, 6, 34, 56]
• t3: [1, 4, 5, 23, 70, 200]
• t4: [5, 14, 78]

当前posting数组为：[2, 2, 0, 3, 0]

根据以上两条信息，可以得到：{t0 : 26, t1 : 4, t2 : 2, t3 : 23, t4 : 5}

则排序后的结果为[t2, t1, t4, t3, t0]

findPivotTerm(terms, θ)

按照之前得到的排序，返回第一个上界累加和≥θ的term。

引入以下数据：[UB0, UB1, UB2, UB3, UB4] = [0.5, 1, 2, 3, 4], θ = 8，UB*为词B*的最大可能的贡献值。

因为(2 + 1 + 4) = 7 < 8 而 (2 + 1 + 4 + 3) = 10 > 8，所以此函数返回t3

pickTerm(terms[0..pTerm])

在0到pTerm(不包含pTerm)中选择一个term。

还是用之前的数据，则是在[t2, t1, t4](没有t3)中选择一个term返回。

关于选择策略，当然是以可以跳过最多的文档为指导，论文中选择了idf最大的term。

上面的过程可以用下图表示：

　　

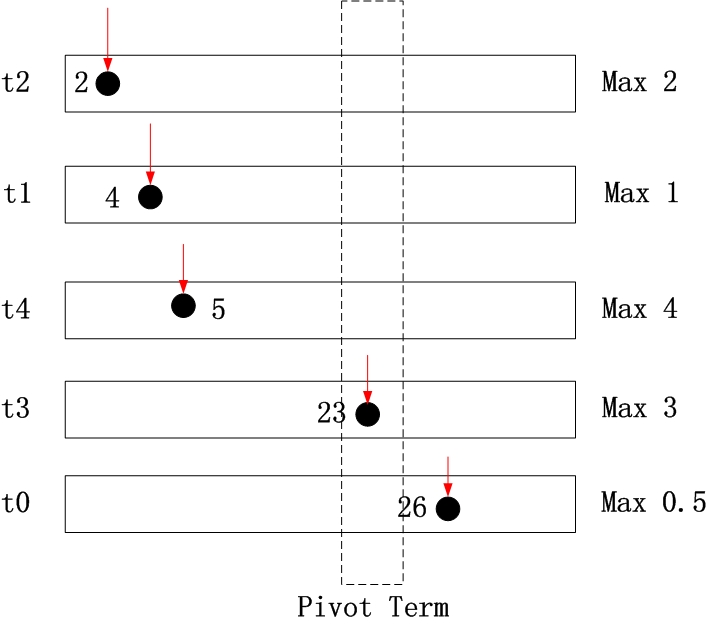
　　上图即为已经按照term当前指向的doc id排序的情况。

对于doc 2，其可能的最大得分为2<8   //2:max of t2

对于doc 4，其可能的最大得分为2+1=3<8 //1:max of t1

对于doc 5，其可能的最大得分为2+1+4=7<8 //4:max of t4

对于doc 23，其可能的最大得分为2+1+4+3=10>8 //3:max of t3

因此，doc 23即为我们需要寻找的pivot term

　　上图其实也解释了为什么要寻找pivot term，因为doc 2、doc 4、doc 5的得分不可能达到threshold，所以可以直接忽略，t2、t1、t4对应的posting list直接skip到doc 23(大于等于doc23的位置)，具体选择先跳哪个，可以根据term的idf来选择，当然也可以按照其距离pivot对于的doc id距离选择，选择一个跳的最多的。在这里，doc 23 被称为pivot，可以作为候选文档（candidate），进一步计算全局得分（evaluate）；doc 2、doc 4、doc 5被跳过。

解释了以上几个函数之后，理解上边的伪码应该没有问题。至于要理解为什么这样不会错过相似度大的文档，就需要自己动一翻脑子。可以参考论文中的解释，不过说起来比较啰嗦，这里就不证明了。

最后要提到的一点是，在sort函数中是没有必要完全排序的，因为每一次循环都只是改变了posting中的一条数据，只要把这个数据排好序就可以了。

附python代码

 

#!/usr/bin/env python
#wand, assume threshold is 4,the upper bound of every term is UB

#max contribute

import time
import heapq

UB = {"t0":0.5,"t1":1,"t2":2,"t3":3,"t4":4} #upper bound of term's value
MAX_RESULT_NUM = 3 #max result number 

class WAND:
    #initial index
    def __init__(self, InvertIndex, last_docid):
        self.result_list = [] #result list
        self.invert_index = InvertIndex #InvertIndex: term -> docid1, docid2, docid3 ...
        self.current_doc = 0
        self.current_invert_index = {} #posting
        self.query_terms = []
        self.threshold = -1
        self.sort_terms = []
        self.LastID = 2000000000 #big num
        self.last_docid = last_docid
    
    #get index list according to query term
    def __InitQuery(self, query_terms):
        self.current_doc = -1
        self.current_invert_index.clear()
        self.query_terms = query_terms
        self.sort_terms[:] = []
        
        for term in query_terms:
            #initial start pos from the first position of term's invert_index
            self.current_invert_index[term] = [ self.invert_index[term][0], 0 ] #[ docid, index ]
    
    #sort term according its current posting doc id
    def __SortTerms(self):
        if len(self.sort_terms) == 0:
            for term in self.query_terms:
                if term in self.current_invert_index:
                    doc_id = self.current_invert_index[term][0]
                    self.sort_terms.append([ int(doc_id), term ])
        self.sort_terms.sort()

    #select the first term in sorted term list
    def __PickTerm(self, pivot_index):
        return 0

    #find pivot term
    def __FindPivotTerm(self):
        score = 0
        #print "sort term ", self.sort_terms  #[docid, term]
        for i in range(0, len(self.sort_terms)):
            score = score + UB[self.sort_terms[i][1]]
            if score >= self.threshold:
                return [ self.sort_terms[i][1], i] #[term, index]

        return [ None, len(self.sort_terms)]

    #move to doc id >= docid
    def __IteratorInvertIndex(self, change_term, docid, pos):
        doc_list = self.invert_index[change_term]
        i = 0
        for i in range(pos, len(doc_list)):
            if doc_list[i] >= docid:
                pos = i
                docid = doc_list[i]
                break

        return [ docid, pos ]

    
    def __AdvanceTerm(self, change_index, docid ):
        change_term = self.sort_terms[change_index][1]
        pos = self.current_invert_index[change_term][1]
        (new_doc, new_pos) = self.__IteratorInvertIndex(change_term, docid, pos)
        
        self.current_invert_index[change_term] = [ new_doc , new_pos ]
        self.sort_terms[change_index][0] = new_doc

    def __Next(self):
        if self.last_docid == self.current_doc:
            return None
        
        while True:
            #sort terms by doc id
            self.__SortTerms()
            
            #find pivot term > threshold
            (pivot_term, pivot_index) = self.__FindPivotTerm()
            if pivot_term == None:
                #no more candidate
                return None
            
            pivot_doc_id = self.current_invert_index[pivot_term][0]
            
            if pivot_doc_id == self.LastID: #!!
                return None
            
            if pivot_doc_id <= self.current_doc:
                change_index = self.__PickTerm(pivot_index)#always retrun 0
                self.__AdvanceTerm( change_index, self.current_doc + 1 )
            else:
                first_docid = self.sort_terms[0][0]
                if pivot_doc_id == first_docid:
                    self.current_doc = pivot_doc_id
                    return self.current_doc
                else:
                    #pick all preceding term,advance to pivot
                    for i in range(0, pivot_index):
                        change_index = i
                        self.__AdvanceTerm( change_index, pivot_doc_id )

    def __InsertHeap(self,doc_id,score):
        if len(self.result_list)<3:
            heapq.heappush(self.result_list, (score, doc_id))
        else:
            if score>self.result_list[0][0]: #large than mini item in heap
                heapq.heappop(self.result_list)
                heapq.heappush(self.result_list, (score, doc_id))
        return self.result_list[0][0]

    #full evaluate the doucment, get its full score, to be added
    def __FullEvaluate(self, docid):
        return 4

    def DoQuery(self, query_terms):
        self.__InitQuery(query_terms)
        while True:
            candidate_docid = self.__Next()
            if candidate_docid == None:
                break
            print "candidate_docid:" + str(candidate_docid)
            #insert candidate_docid to heap
            full_doc_score = self.__FullEvaluate(candidate_docid)
            mini_item_value = self.__InsertHeap(candidate_docid, full_doc_score)
            #update threshold
            self.threshold = mini_item_value
            print "result list ", self.result_list
        return self.result_list

if __name__ == "__main__":
    testIndex = {}
    testIndex["t0"] = [ 1, 3, 26, 2000000000]
    testIndex["t1"] = [ 1, 2, 4, 10, 100, 2000000000 ]
    testIndex["t2"] = [ 2, 3, 6, 34, 56, 2000000000 ]
    testIndex["t3"] = [ 1, 4, 5, 23, 70, 200, 2000000000 ]
    testIndex["t4"] = [ 5, 14, 78, 2000000000 ]
    
    last_doc_id = 100
    w = WAND(testIndex, last_doc_id)
    final_result = w.DoQuery(["t0", "t1", "t2", "t3", "t4"])
    print "final result "
    for item in final_result:
        print "doc " + str(item[1])

 

 

附录每一步的执行过程，如果原来的设置，是0结果的，因此设置threshold为4：

初始位置：

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

　　posting=[1,1,2,1,5]，也就是{t0:1,t1:1,t2:2,t3:1,t4:5}

　　cur_doc = 0

第1步：

1. 按照posting的doc id对term升序排序，这里得到[t0,t1,t3,t2,t4]
2. 寻找pivot，0+1+3=4>=4, 也就是到了t3大于等于4，因此t3就是pivot term，pivot就是其对应的doc id=1
3. pivot为1，cur doc id=0，因此pivot>cur_doc, 然后比较posting[0].doc_id，也就是t0对应的当前doc id=1 和pivot=1是否相等，这里相等，then，返回doc1, cur_doc_id=1

　　当前的数据不变：

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

　　posting=[26,1,2,1,5]，也就是{t0:26,t1:1,t2:2,t3:1,t4:5}

　　cur_doc = 0

 

第2步：

1. 按照posting的doc id对term升序排序，这里得到[t0,t1,t3,t2,t4]
2. 寻找pivot，0+1+3=4>=4, 也就是到了t3大于等于4，因此t3就是pivot term，pivot就是其对应的doc id=1
3. pivot为1，cur doc id=1，因此pivot<=cur_doc, ，then，选择一个pterm之前的term，向前移动。这里选择第一个，也就是t0，然后将其对应的倒排指针移动到大于等于doc_cur_id+1的位置，这里移动到3.

　　当前的数据：

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

　　posting=[3,1,2,1,5]，也就是{t0:3,t1:10,t2:2,t3:1,t4:5}

 

后续的步骤基本差不多

第3步， 排序后[t1,t3,t2,t0,t4] cur_doc = 1,pivot term=t1, pivot=1，移动t1

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

 

第4步, 排序后[t3,t2,t1,t0,t4] cur_doc = 1,pivot term=t3, pivot=1，移动t3

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

 

 

第5步, 排序后[t1,t2,t0,t3,t4] cur_doc = 1,pivot term=t3, pivot=4,移动t1

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

第6步，排序后[t2,t0,t1,t3,t4] cur_doc = 1,pivot term=t3 pivot=4，移动t2

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

第7步，排序后[t0,t1,t3,t2,t4] cur_doc = 1,pivot term=t3 pivot=4，移动t0

• t0: [1, 3, 26]                   max:0
• t1: [1, 2, 4, 10, 100]       max:1
• t2: [2, 3, 6, 34, 56]         max:2
• t3: [1, 4, 5, 23, 70, 200] max:3
• t4: [5, 14, 78]                 max:4

第7步，排序后[t1,t3,t4,t2,t0] cur_doc = 1,pivot term=t3 pivot=4

此时posting[0].did，也就是t1对倒排列表指针指向doc id=4==pivot=4

因此，返回doc_id=4,cur_doc_id=4

至此已经得到两个结果文档，即为1和4

后续可以以此类推

可以继续得到结果5,14,78