神经网络基础

（个人学习所用，内容来源于网络，侵权删）

1. 感知机

感知机由Rosenblatt在1957年提出，是神经网络的基础，该思想受生物学启发（参照下图），

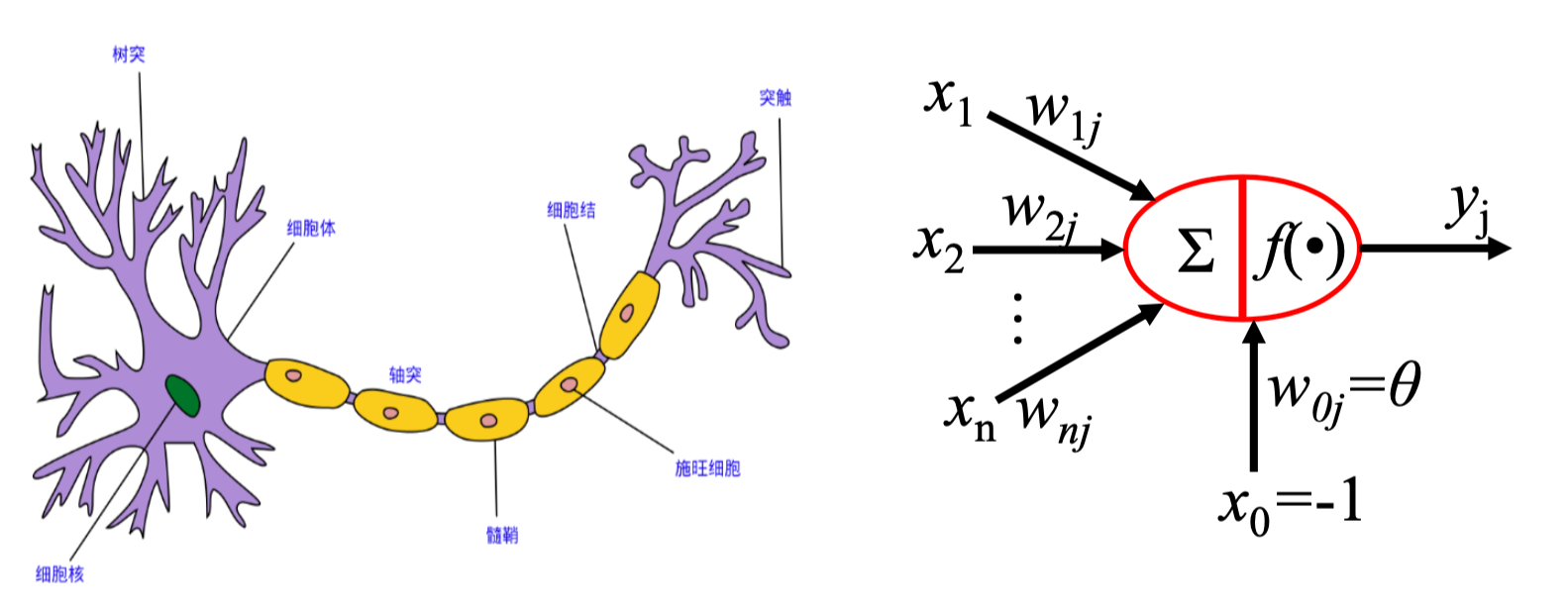
在其看来，人的大脑可以看作一个生物的神经网络，其最小的单元是神经元。人的神经网络由这样的一些神经元组成，它接受一些信号，这些信号可能是眼睛看到的光学信号或者耳朵听到的声学信号，这些信号到树突组织后会产生一些生物电，形成一些刺激，细胞核就对这些刺激信号进行处理，然后通过轴突组织输出处理的结果，传递给其他组织。以上就是人脑的一个神经元进行感知的大致工作原理。

根据上面的原理，一个简单的感知机如下图所示：

**2. 多层感知机**

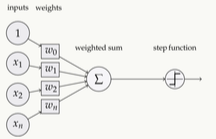
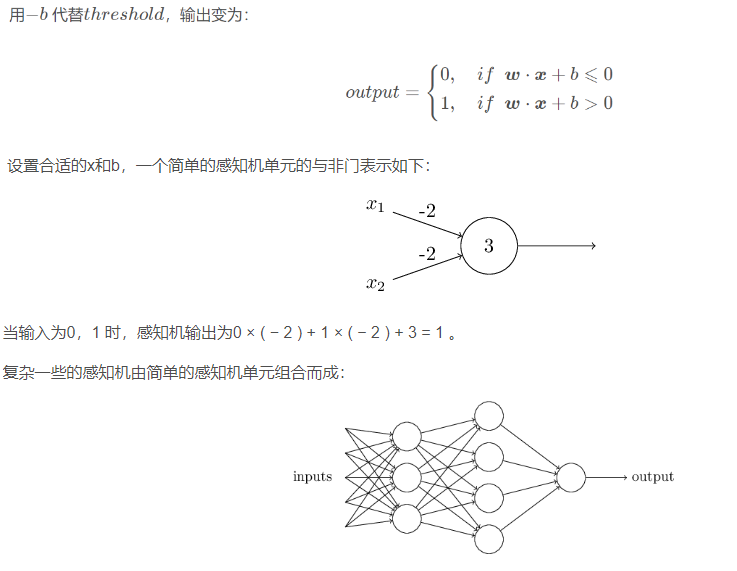
多层感知机就是在单个感知机的基础上进行推广，最突出的特点就是拥有多个神经元层，因此也叫深度神经网络，相较于单独的感知机，多层感知机第i层的每个神经元与第i-1层都有连接。

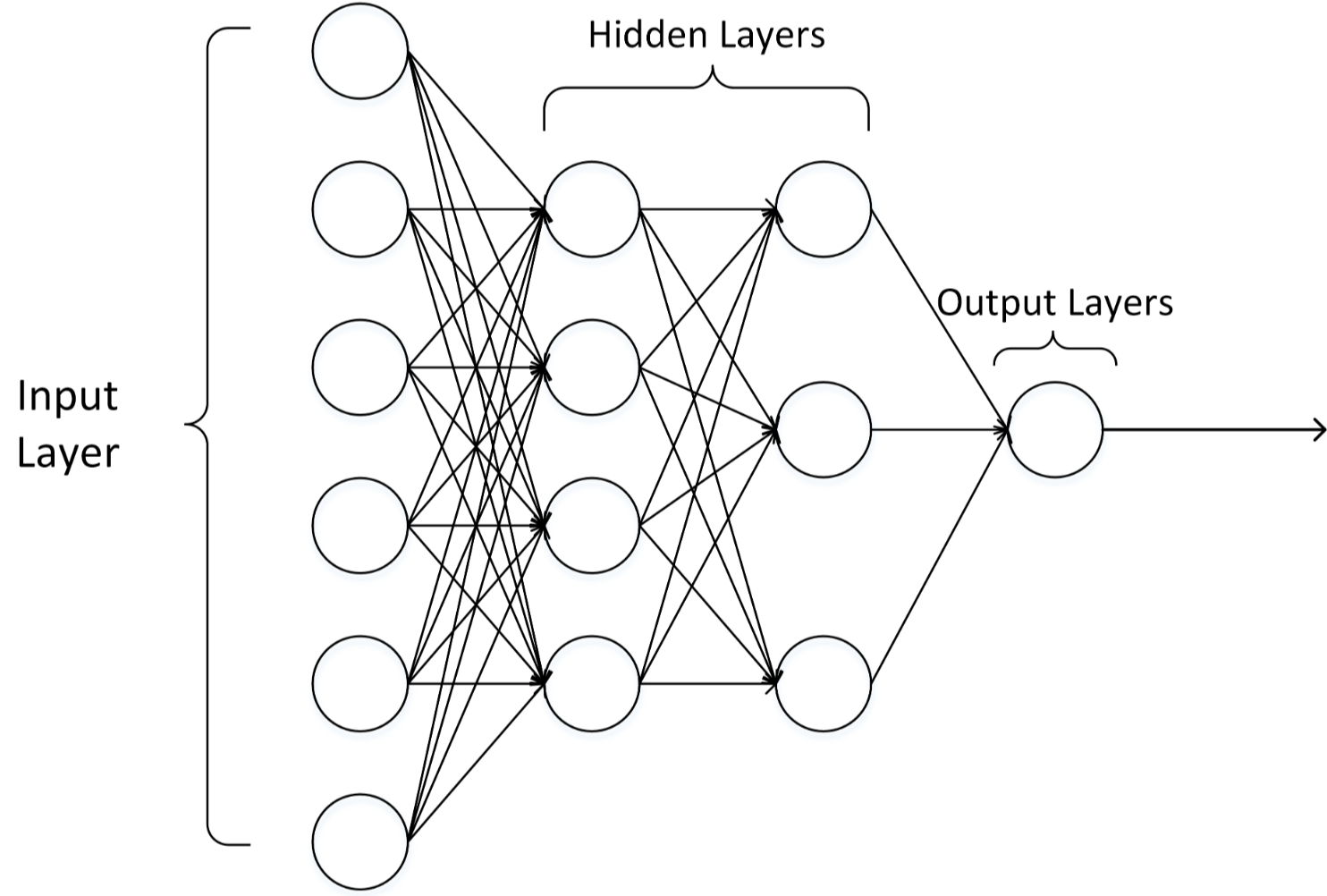
3.神经网络常用模型结构

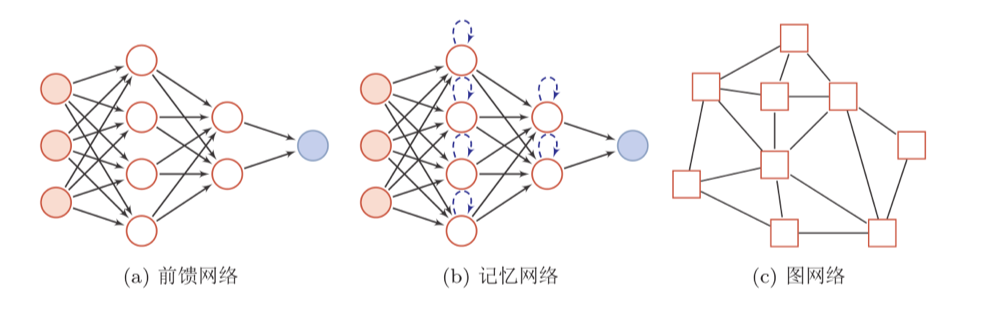
圆形代表一个神经元，方形代表一组神经元。

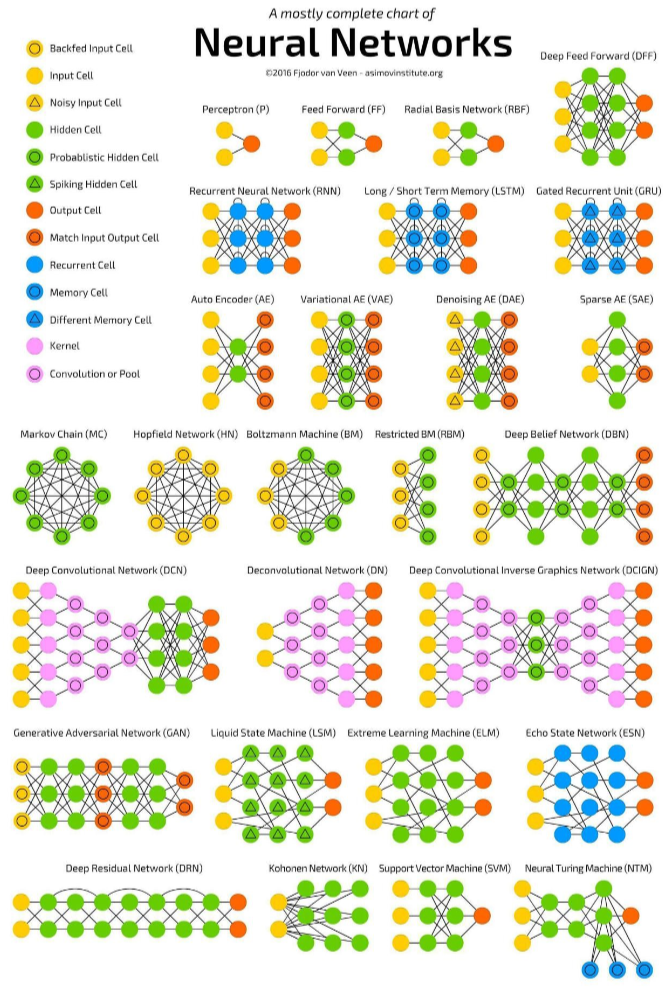
上图包含了大部分常用模型结构。

4.前向传播和反向传播
人工神经网络的神经元本质上由权重参数组成， 因此该网络接收输入，通过逐层计算得到输出，这个过程叫做前向传播(forward propagation)；神经网络前向传播得到的结果会存在误差，因此需要纠正，纠正的方法就是通过计算梯度更新网络参数，寻找最优解这个过程叫做反向传播。

前向传播

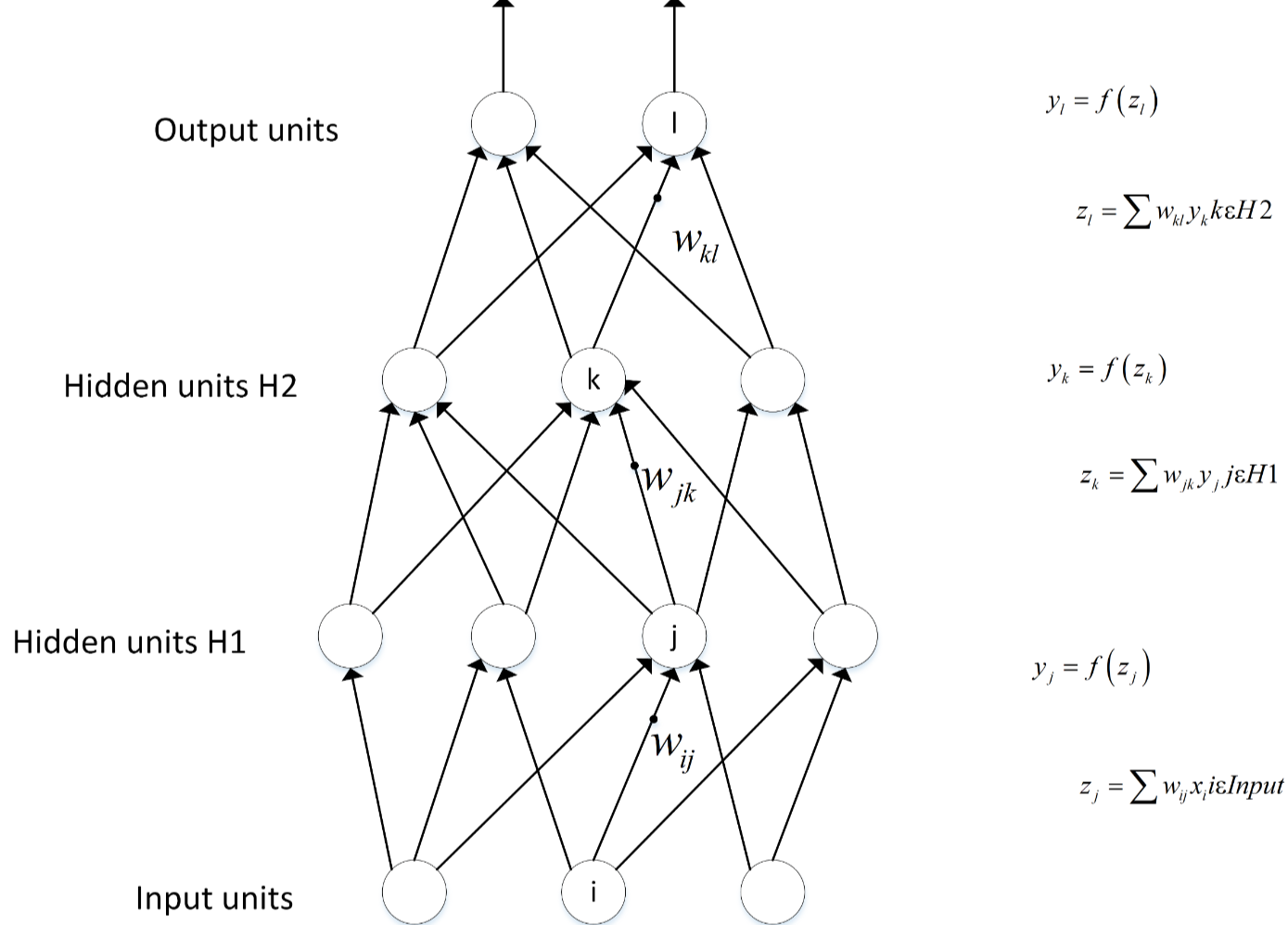
前向传播用数学公式表示就是\(Y=f_n(W_n*(...f_2(W_2*(f_1(W_1*X_1+B_1))+B_2))+B_n)\)，其中\(Y\)是输出结果的矩阵，\(n\)是神经网络的层数，\(W\)是神经网络一层的权重矩阵，\(X\)是输入矩阵，函数\(f\)就是激活函数，例如\(ReLu,Sigmoid\)等等。通过这样一层一层嵌套计算，最终得到一个输出层结果。

代码实现如下：

点击查看代码

# * 表示element-wise乘积，· 表示矩阵乘积

class Layer:
    '''中间层类'''
    self.W  # (input_dim, output_dim)
    self.b  # (1, output_dim)
    self.activate(a) = sigmoid(a)/tanh(a)/ReLU(a)/Softmax(a)

    def forward(self, input_data):       # input_data: (1, input_dim)
       '''单个样本的前向传播'''
       input_data · self.W + self.b = a  # a: (1, output_dim)
       h = self.activate(a)              # h: (1, output_dim)
       return h

反向传播

梯度下降法原理

“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）

将神经网络看作一个数学公式，这个数学公式的所有结果组成一个结果空间，我们想要的就是在通过前向传播得到一个输出结果\(Y_p{re}\)之后，这个输出和真实值\(Y_{true}\)之间会存在一个误差，我们想要的就是寻找一个\(Y_pre\)，使得与真值之间的误差最小。寻找的方法就是梯度下降法。

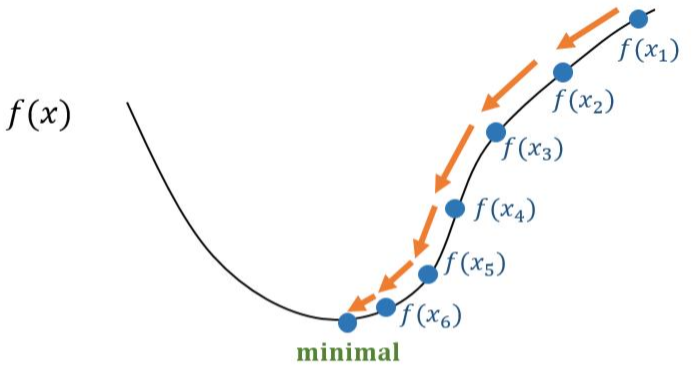
如图所示，当结果是\(f(x_1)\)时，其离最小值很远，要到达minimal，需要使用梯度下降法，具体原理如下

实际的神经网络不会是单一的权重参数，而是非常多的权重参数，但原理是相通的，假如有\(x_1\)，\(x_2\)两个参数，\(x_1\)求一个梯度决定在\(x_1\)轴下降的方向，\(x_2\)同样有一个梯度决定其下降的方向，这两个梯度组成的向量就告诉我们函数应该向结果空间的哪个方向下降，通过求偏微分即可得到每一个权重参数的梯度，继而更新参数。图中的\(\alpha\)代表沿着梯度方向前进的步长，其值过大时可能会使得函数直接跨过最小值。

代码实现如下：

点击查看代码

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt


def f(x):
    return np.power(x, 2)

def d_f_1(x):
    return 2.0 * x

def d_f_2(f, x, delta=1e-4):
    return (f(x+delta) - f(x-delta)) / (2 * delta)


# plot the function
xs = np.arange(-10, 11)
plt.plot(xs, f(xs))
plt.show()

learning_rate = 0.1
max_loop = 30

x_init = 10.0
x = x_init
lr = 0.1
for i in range(max_loop):
    # d_f_x = d_f_1(x)
    d_f_x = d_f_2(f, x)
    x = x - learning_rate * d_f_x
    print(x)

print('initial x =', x_init)
print('arg min f(x) of x =', x)
print('f(x) =', f(x))

参考来源：
深度学习知识点全面总结