径向基神经网络(RBF)

1. 径向基函数（Radical Basis Function）

1.1 定义

• 径向基函数是一个取值仅仅依赖于离某点距离的实值函数
  • 距离原点：$ \phi(x) = \phi(||x||)$
  • 距离任一点c（中心点）：\(\phi(x,c) = \phi(||x-c||)\)

1.2 常用的三种径向基函数

1.2.1 Gauss（高斯）函数

• \(\varphi(r) = exp(-\frac{r^{2}}{2\sigma^{2}})\)

1.2.2 反演S型函数

• $ \varphi(r) = \frac{1}{1 + {exp(\frac{r ^ {2}}{\sigma ^ {2} } ) } } $

1.2.3 拟多二次函数

• \(\varphi(r) = \frac{1}{(r^{2}+ \sigma^{2} ) ^ {1/2}}\)

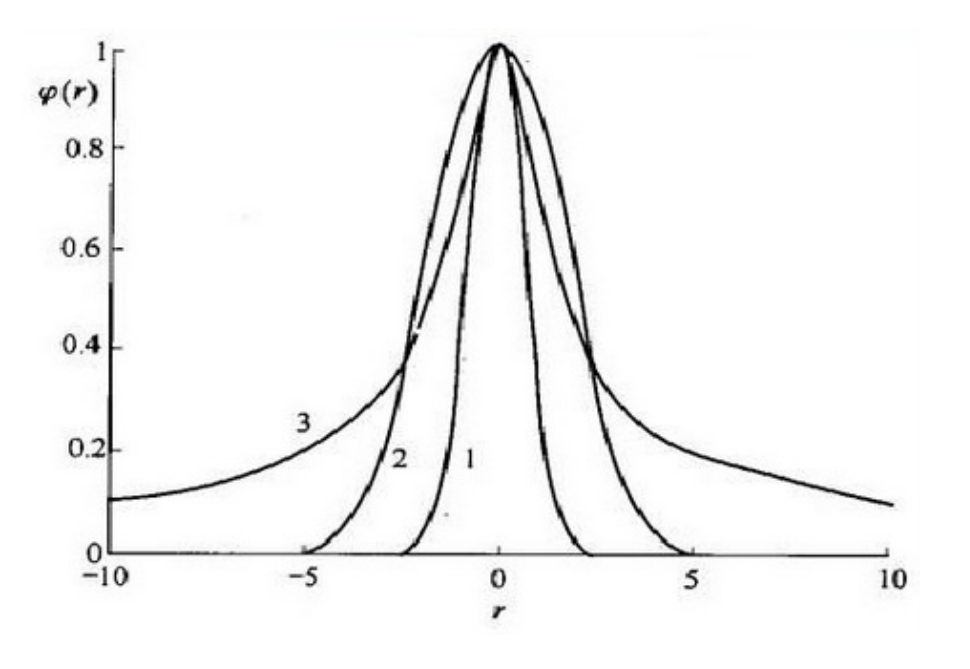
\(\sigma称为基函数的扩展函数或宽度,\sigma越小，\)积函数的宽度越小，基函数就越有选择性。

神经元的输入离径向基函数中心越远，神经元的激活程度就越低

2. 径向基（RBF）神经网络

• 径向基网络也是前馈型神经网络的一种，但它的设计思想和BP网络完全不一样
• RBF网络是一种单隐层前馈神经网络，它使用径向基函数作为隐层神经元激活函数，而输出层则是对隐层神经元输出的线性组合

2.1 RBF神经网络的原理

Cover 定理：将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。

2.2 RBF神经网络的基本结构

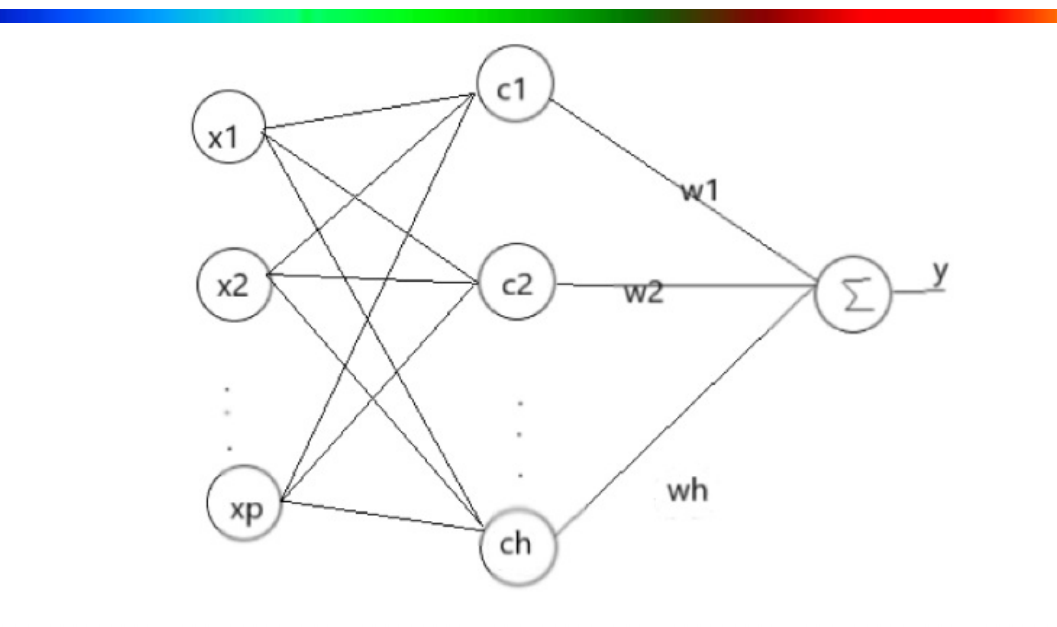
• 三层神经网络：输入层、输出层以及一个隐层
• 隐层节点激活函数为径向基函数，输出节点激活函数为线性函数
• 输入层与隐层无权连接，隐层与输出层是线性加权，即网络可调参数
• 输入X是个p维的向量，隐层节点数为h，h > p
• 隐层节点的输入为输入向量与节点中心的距离（范数）而非向量内积，且节点中心不可调
• 隐层节点的非线性变换把向量从低维p映射到高维h，把线性不可分问题转变为线性可分问题
• 隐层节点参数确定后，输出权值可通过解线性方程组得到

2.3 径向基神经网络的激活函数

• 径向基神经网络的激活函数可表示为：
  \(R(x_{p} - c_{i}) = exp(-\frac{1}{2\sigma^{2}}||x_{p} - c_{i}||) ^ {2}\)

• 径向基神经网络的结构可得到网络的输出为：
  $ y_{j} = \sum_{i=1}^ {h} w_ {i} exp (-\frac{1}{ 2\sigma^{2} } || x_{j} - c_{i}|| ) $

• 其中\(x_{j}为p维输入样本，c_{i}为p维中心向量（待确定量）\)，h为隐含层的结点数

2.4 逻辑运算异或的实现

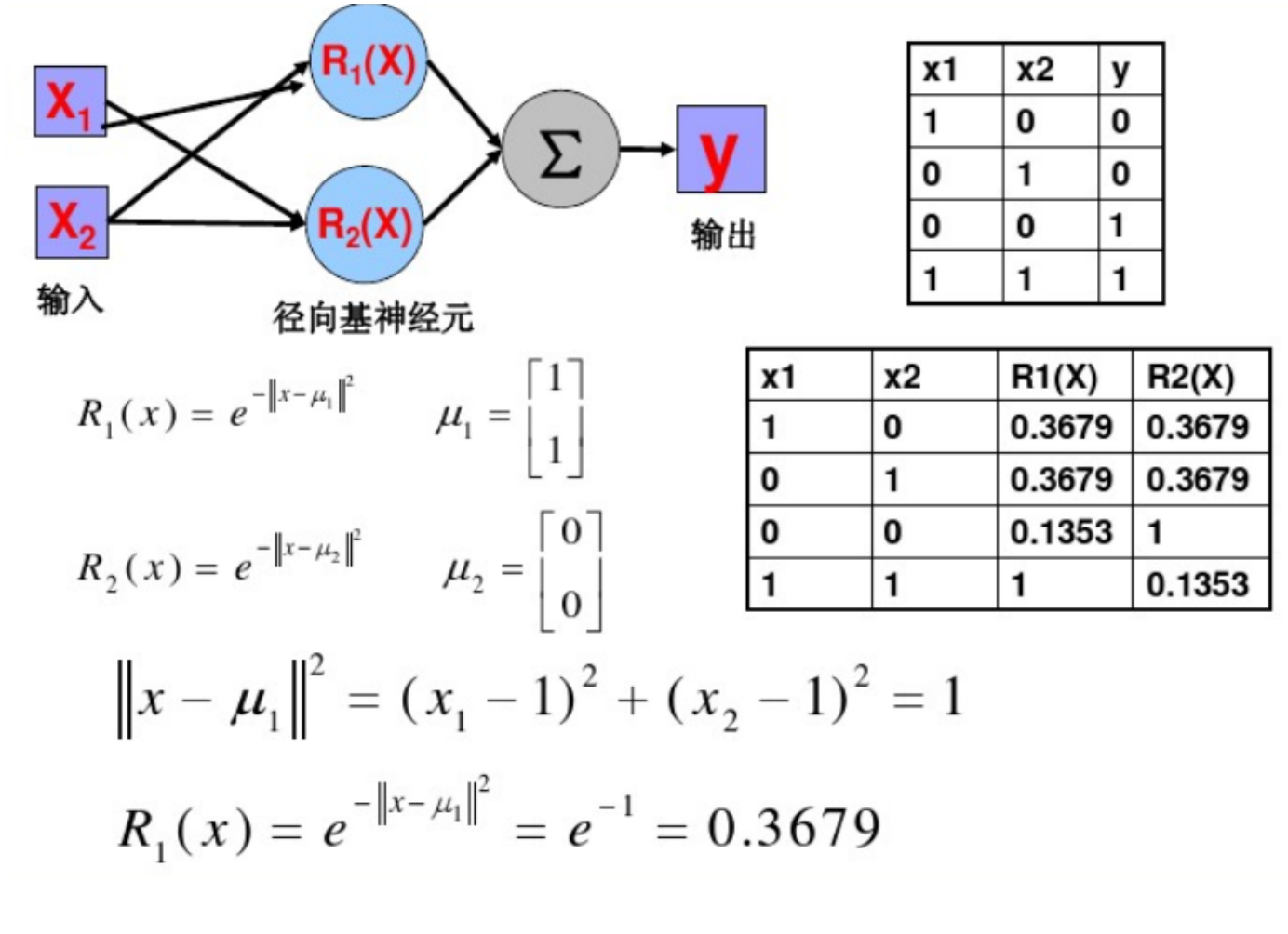
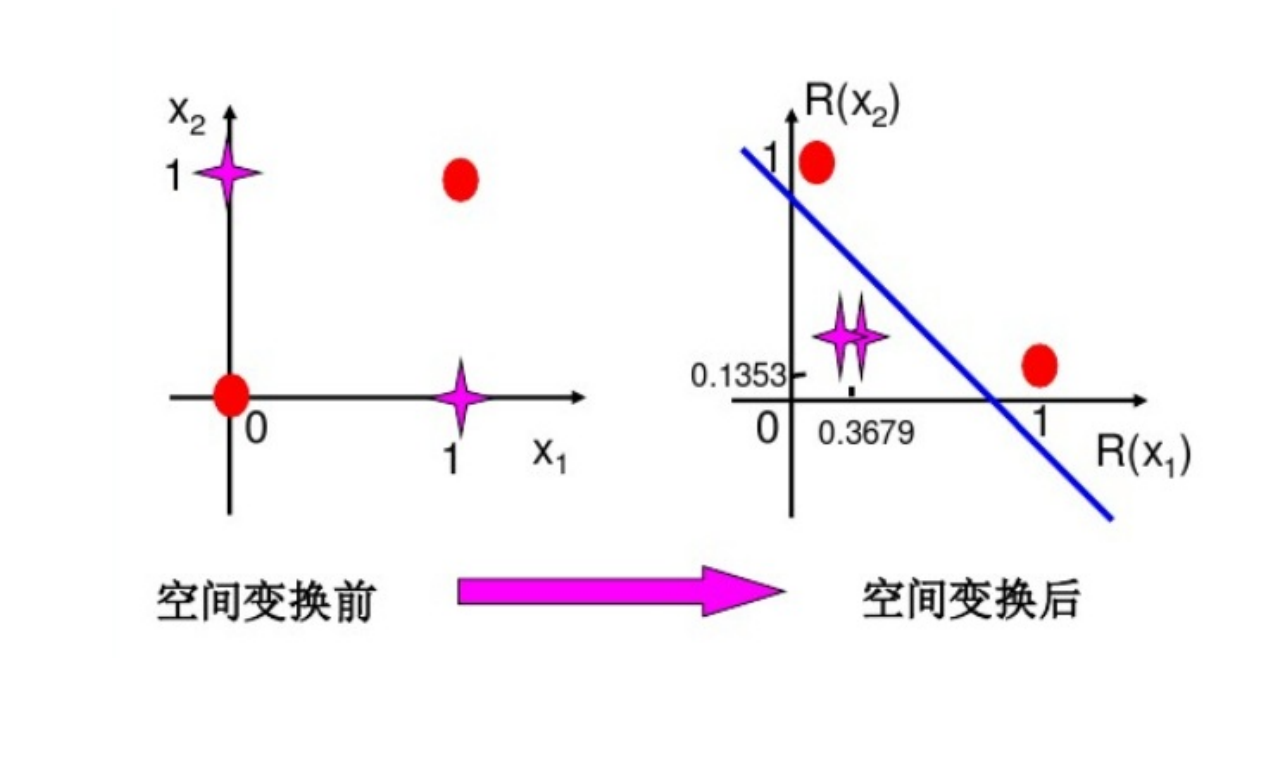
3. RBF网络学习问题

3.1 RBF网络学习的三类参数

3.2 基函数中心选取方法

1. 随机选取法：从样本中选取

• 一般来说，样本密集的地方中心点可以适当多些，样本稀疏的地方中心点可以少些;若数据本身是均匀分布的，中心点也可以均匀分布。总之，选出的数据中心应具有代表性，
• 径向基函数的扩展常数是根据数据中心的散布而确定的，为了避免每个径向基函数太尖或太平，一种选择方法是将所有径向基函数的扩展常数设为。$ \sigma_{i} = \frac{c_{max}}{\sqrt{2h}}$ i= 1,2,… h, cmax为所选取中心点之间的最大距离

2. 自组织中心选取法：K均值聚类

• 常采用各种动态聚类算法对数据中心进行自组织选择，在学习过程中需对数据中心的位置进行动态调节。常用的方法是K-means聚类，其优点是能根据各聚类中心之间的距离确定各隐节点的扩展常数:

3. 监督选取法：
   

4. RBF与BP神经网络的区别

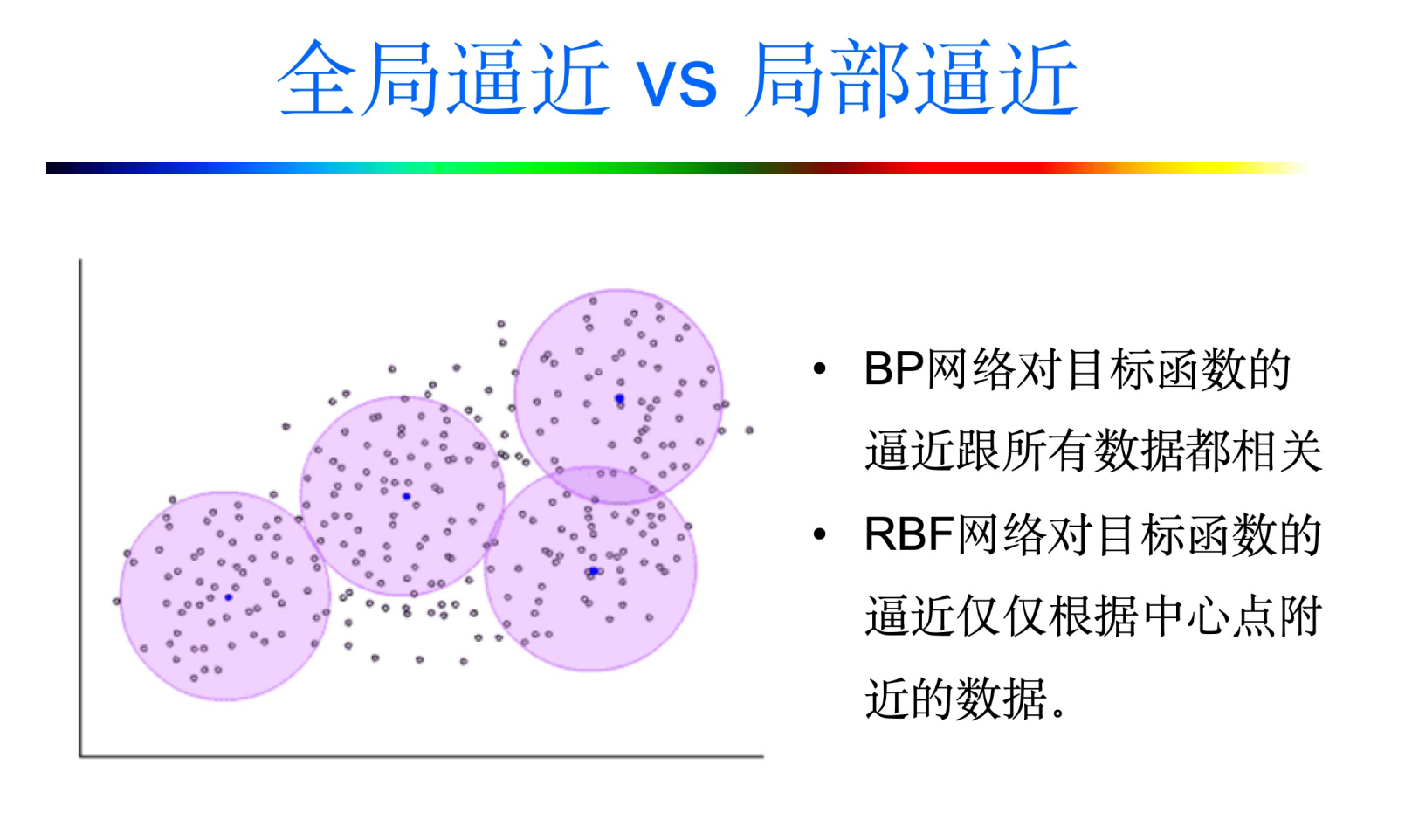
4.1 全局逼近网络

• 当神经网络的一个或多个可调参数（权值和阈值）对任何一个输出都有影响，则称该神经网络为全局逼近网络
• 对于每次输入，网络上的每一个权值都需要调整，从而导致全局逼近网络的学习速度很慢
• 如BP网络，每个隐层神经元的输出均属于（0，1）

4.2 局部逼近网络

• 对网路输入空间的某个局部区域只有少数几个连接权值影响网络的输出，则称该网络为局部逼近网络
• 学习速度快，有可能满足有实时性要求的应用
• 如RBF网络，如果输入样本在扩展宽度之外，则径向基函数值为0，对网络输出无影响，所以收敛比较快
  

4.3 其他比较

• RBF网络是局部响应的(由于扩展宽度的设置)，而其他前向型网络(如MLP)，激活函数一般都是全局响应函数。由于这样的不同，要实现同样的功能，RBF比BP网络需要更多的神经元，这就是RBF网络不能取代标准前向型网络的原因
• RBF网络只含一个隐层，BP网络可以有多个隐层。
• RBF的训练时间短。它对函数的逼近是最优的，可以以任意精度逼近任意连续非线性函数。隐层中的神经元越多，逼近越精确。
• RBF具有唯一最佳逼近的特性
• RBF网络中合适的隐层节点数、节点中心及宽度不易确定

5. RBF神经网络与SVM的区别

6. RBF网络的应用

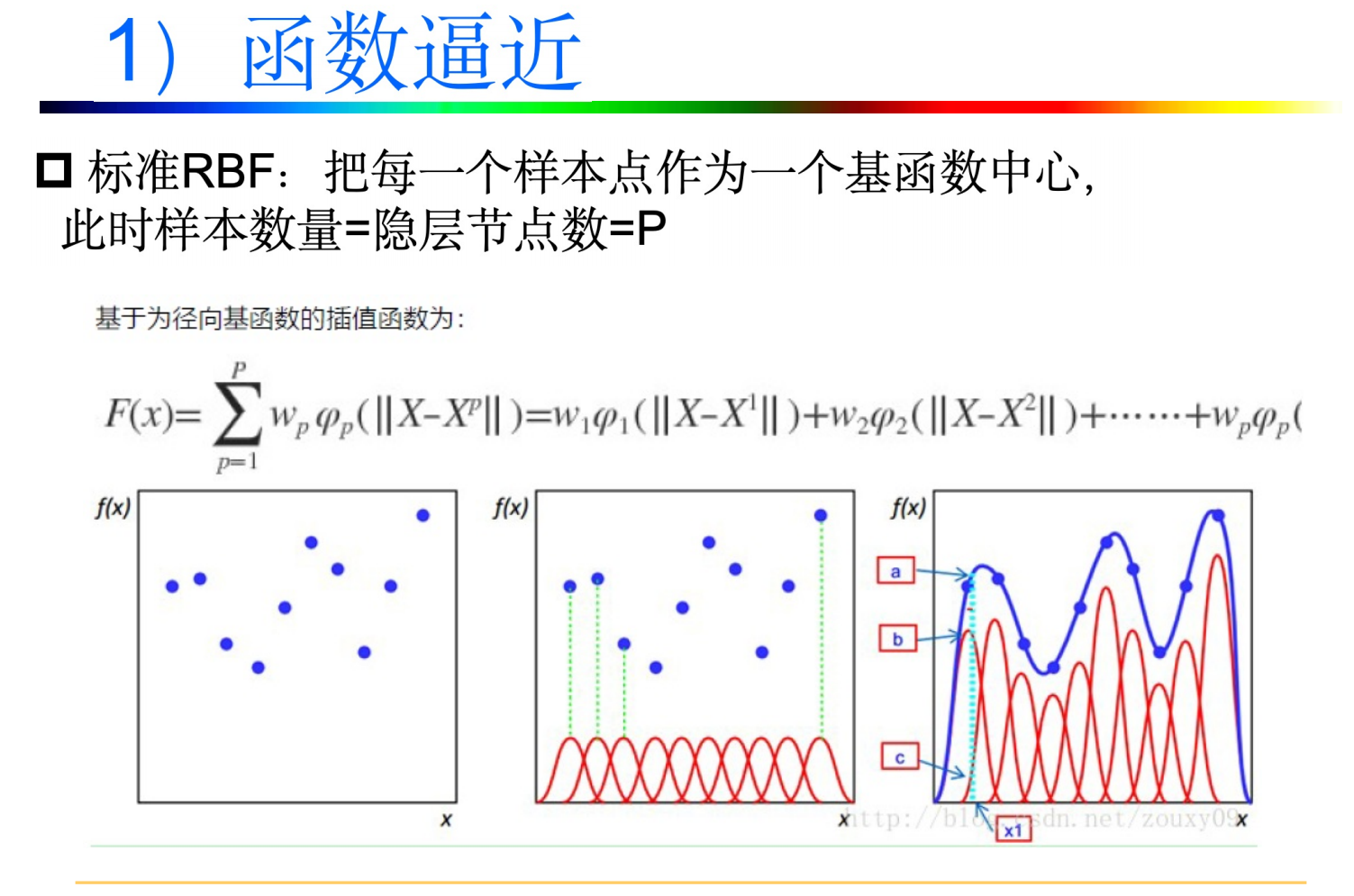
6.1 函数逼近

• 以任意精度逼近任一连续函数。一般函数都可以表示为一组基函数的线性组合。RBF网络相当于用隐层节点的输出构成一组基函数，然后用输出层来进行线性组合，以完成逼近功能。
  

6.2 分类问题

• 解决非线性可分问题。RBF网络用隐层单元先将非线性可分的输入空间设法变换到线性可分的特征空间（通常是高维空间）使得在低维空间内的线性不可分问题在高维空间内线性可分，然后用输出层来进行线性划分，完成分类功能。