「学习笔记」一维树状数组
树状数组是一种查询和修改都是 $O_{logn} $ 的数据结构
树状数组可以做到单点修改区间查询,单点查询区间修改和区间修改区间查询
树状数组也分一维和二维
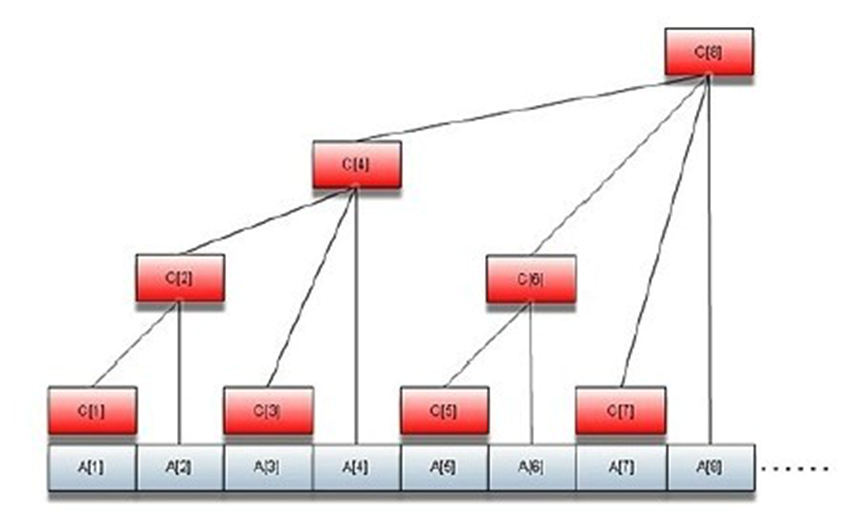
由此可以看出
\(C_1 =A_1\)
\(C_2 = A_1 + A_2\)
\(C_3 = A_3\)
\(C_4 = A_1 + A_2 + A_3 + A_4\)
\(C_5 = A_5\)
\(C_6 = A_5 + A_6\)
\(C_7 = A_7\)
\(C_8 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 + A_7 + A_8\)
\(......\)
要时刻记着每个点是怎么来的,否则后面容易混!!!
设节点编号为 $n$,那么,它所管辖的区域就是 $2^j$($j$ 是 $n$ 的二进制形式的末尾 $0$ 的个数) 子节点找父节点就是加上最后一个 $1$\(e.g.\)
\(1->2\)—— \(0001 + 0001 = 0010\)
\(2->4\)—— \(0010 + 0010 = 0100\)
\(3->4\)—— \(0011 + 0001 = 0100\)
那现在问题来了,怎么求最后一个 \(1\) ?
通常,我们把它叫做 \(\text{lowbit(n)}\)
计算方法 n & (-n)
&: 位运算符,按位与,只有参与运算的两个二进制数所对应的二进制位均为 \(1\) ,结果对应位才为 \(1\) ,否则为 \(0\)
ll lowbit(ll x)
{
return x&(-x);
}
单点修改,区间查询:
问题:在 \(x\) 位置加上 \(y\),求 \(a\),\(b\)的区间和。
如果 \(x\) 位置加上 \(y\),那么,它的父节点也要加上 \(y\),查询父节点位置前面已经提到了,这个操作叫单点修改。
单点修改代码:
void add(ll x,ll y)//数组x位置加y
{
for(rll i=x;i<=n;i+=(i&(-i)))
{
s[i]+=y;//逐层向上修改(毕竟子节点改了,父节点也要改)
}
}
建树的过程,就可以看作是单点修改。
区间查询,就是找类兄弟
\(e.g.\) (\(sum\) 可以看作前缀和)
\(sum_5 = S_5 + S_4 + 0\)
\(S_5:0101\)
\(S_4:0100\)
\(0:0000\)
\(sum_7 = S_7 + S_6 + S_4 + 0\)
\(S_7:0111\)
\(S_6:0110\)
\(S_4:0100\)
\(0:0000\)
发现了吗,找类兄弟就是减去最后一个 \(1\) ,直至没有 \(1\) 为止
区间查询代码:
ll sum(ll x)
{
ll ans=0;
for(rll i=x;i;i-=(lowbit(i)))
{
ans+=s[i];
}
return ans;
}
单点修改,区间查询完整代码(有注释):
#include<bits/stdc++.h>
#define ll long long
#define rll register long long
using namespace std;
ll n,m,a;
ll s[1000100];
void add(ll x,ll y)//数组x位置加y
{
for(rll i=x;i<=n;i+=(i&(-i)))
{
s[i]+=y;//逐层向上修改(毕竟子节点改了,父节点也要改)
}
}
ll sum(ll x)
{
ll ans=0;
for(rll i=x;i;i-=(i&(-i)))
{
ans+=s[i];//求和,找类兄弟
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(rll i=1;i<=n;++i)
{
scanf("%lld",&a);
add(i,a);//建树过程,把操作之前的树上的点都看作是0
}
for(rll p,l,r,i=1;i<=m;++i)
{
scanf("%lld%lld%lld",&p,&l,&r);
if(p==1)
{
add(l,r);//在l位置加上r
}
else
{
printf("%lld\n",sum(r)-sum(l-1));//查询区间[l-r]
}
}
return 0;
}
区间修改,单点查询:
区间修改主要运用差分思想
注意,后面的内容必须会差分才可以看懂,不会差分的请止步。
区间修改代码(差分):
void add(ll x,ll y)
{
for(rll i=x;i<=n;i+=(i&(-i)))
{
s[i]+=y;
}
}
单点查询,运用差分求和的思想,\([1-i]\) 的差分和就是第i个元素的数值
单点修改代码:
ll sum(ll x)
{
ll ans=0;
for(rll i=x;i;i-=(i&(-i)))
{
ans+=s[i];//利用差分的思想求和,1-i的差分数组的和就是第i个数的值
}
return ans;
}
区间修改,单点查询完整代码(有注释):
#include<bits/stdc++.h>
#define ll long long
#define rll register long long
using namespace std;
ll n,m,last,a;
ll s[1000100];
void add(ll x,ll y)//差分数组x的位置加y
{
for(rll i=x;i<=n;i+=(i&(-i)))
{
s[i]+=y;
}
}
ll sum(ll x)//求第x个数的数值
{
ll ans=0;
for(rll i=x;i;i-=(i&(-i)))
{
ans+=s[i];//利用差分的思想求和,1-i的差分数组的和就是第i个数的值
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(rll i=1;i<=n;++i)
{
scanf("%lld",&a);
add(i,a-last);//记录差分数组
last=a;//更新last,记录差分
}
for(rll p,l,r,j,i=1;i<=m;++i)
{
scanf("%lld",&p);
if(p==1)
{
scanf("%lld%lld%lld",&l,&r,&j);//在区间[l-r]中,每一个元素加j
add(l,j);//差分数组s[l]+j
add(r+1,-j);//差分数组s[r+1]-j
}
else
{
scanf("%lld",&j);
printf("%lld\n",sum(j));//求点j的值,利用差分求和
}
}
return 0;
}
区间修改,区间查询:
这里的区间修改依然是差分思想,但求的是区间和,因此,与上面的有不同
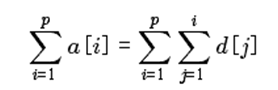
区间和就是这个区间的数都加一遍, \(d(j)\) 是差分数组,差分数组从 \(1\) 到 \(i\) 的和就是 \(a(i)\)
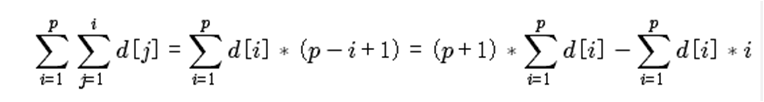
这里要自己亲自加一遍试试,全加起来,就会发现,\(d(1),d(2),d(3)...\) 被加的个数有规律,最后用分配律,就是最终公式了。
公式一定要记住!!!
由此可见,区间修改,区间查询需要多维护一个 $d(i) \times i$ 的和值区间修改代码:
void add(ll x,ll y)//差分数组x位置的数加y
{
for(rll i=x;i<=n;i+=(i&(-i)))
{
s1[i]+=y;//记录差分
s2[i]+=x*y;//记录差分的和
}
}
区间查询代码:
ll sum(ll x)//求前缀和(准确来说也不是前缀和,但性质差不多)
{
ll ans=0;
for(rll i=x;i;i-=(i&(-i)))
{
ans+=(x+1)*s1[i]-s2[i];//根据公式计算
}
return ans;
}
scanf("%lld%lld",&l,&r);//求区间(l-r)的和
printf("%lld\n",sum(r)-sum(l-1));//前缀和计算
区间修改,区间查询完整代码(有注释):
#include<bits/stdc++.h>
#define ll long long
#define rll register long long
using namespace std;
ll n,m,a,last;
ll s1[1000100],s2[1000100];
// s1 记录差分树状数组(公式第一项) s2 记录差分数组×i的和 (公式第二项)
void add(ll x,ll y)//差分数组x位置的数加y
{
for(rll i=x;i<=n;i+=(i&(-i)))
{
s1[i]+=y;//记录差分
s2[i]+=x*y;//记录差分的和
}
}
ll sum(ll x)//求前缀和(准确来说也不是前缀和,但性质差不多)
{
ll ans=0;
for(rll i=x;i;i-=(i&(-i)))
{
ans+=(x+1)*s1[i]-s2[i];//根据公式计算
}
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(rll i=1;i<=n;++i)
{
scanf("%lld",&a);
add(i,a-last);//a-last 计算差分
last=a;//更新last,使得记录的都是后一个数和前一个数的差
}
for(rll p,l,r,j,i=1;i<=m;++i)
{
scanf("%lld",&p);//判断是修改还是查询
if(p==1)
{
scanf("%lld%lld%lld",&l,&r,&j);//l-r区间的元素加j
add(l,j);//差分数组s1[l]+j
add(r+1,-j);//差分数组s1[r+1]-j
}
else
{
scanf("%lld%lld",&l,&r);//求区间(l-r)的和
printf("%lld\n",sum(r)-sum(l-1));//前缀和计算
}
}
return 0;
}
喜欢的话,还请支持一下吧,写的不好,dalao 勿喷QWQ


 浙公网安备 33010602011771号
浙公网安备 33010602011771号