最短路
https://csacademy.com/app/graph_editor/
https://riverhamster.gitee.io/app/graph_editor/
graph.changwenxuan.cn/app/graph_editor 傻逼搭的网站,慢的要死
upd 24/1/5 最有侮辱性的一集
注:时间复杂度分析中,假设 \(n \le m \le n ^ 2\)。
最短路本质上是一种 DP。
阶段:点
状态:拆点
决策:边
最优子结构:最短路的任何子路径都一定是最短路。
无后效性:正权图中一定可以找到一种无后效性的枚举顺序(Dijkstra)。
重复子问题:\(dis_i\) 表示所有以 \(i\) 为结尾的所有路径的长度的最小值。
存图
本来不打算写的,但是发现 vector + O2 跑得比链前快之后真的绷不住了。
主要原因是 vector 比链前慢的地方是在建图是需要动态分配内存,但是存完图后每个点连出的边就储存在一段连续的内存中,利用 cache 机制大量访问会比较快。尤其是在 NKOJ 上。卡常卡不过去可以试试。
upd 24/01/22
某道题目在 NKOJ 用 vector 比链前快 \(3 \sim 4\) 倍,洛谷用 vector 比链前慢 \(\frac{1}{4}\)。NKOJ 稳定发挥。
但是链前真的很酷。
Dijkstra
0. 读音
按照荷兰语读法,Dijkstra 中 j 不发音,读作 \(\text{/ˈdaɪkstrə/}\) 或 \(\text{[ˈdɛikstra]}\)。中文类似“戴克斯特拉”。结尾加颤音。
1. 朴素版
本质上是在正权图中通过贪心的方式找到一种使得 DP 没有后效性的转移顺序。
将所有点分为 \(S\) 和 \(T\) 两个集合,\(S\) 表示最短路确定且不会再更改,\(T\) 表示最短路未确定,最开始所有点都在 \(S\) 中。每次从 \(T\) 找出最短路最小的点,用它更新其他点的最短路,并放进 \(S\) 集合。
因为所有边的边权都是正数,所以每次找出的最小的点肯定不会被其他 \(T\) 集合中的点再更新最短路。
也就是说,每个点一定是以最短路长度从小到大的顺序被放入 \(S\) 集合的,前面一定不会被后面影响。这也是一个 DAG 的拓扑序。
2. 堆优化 / 线段树优化
每次找出 \(T\) 集合中最短路最小的点可以用堆优化,STL 优先队列 \(O(m \times \log m)\),手写二叉堆 \(O(m \times \log n)\),斐波那契堆 \(O(n \times \log n + m)\)。
不会手写堆可以线段树,也是 \(O(m \times \log n)\)。但线段树实际上一般比 STL 更慢(NKOJ 不加快读甚至会 TLE),因为一定会把 \(O(m \times \log n)\) 跑满,但是一般不会有毒瘤出题人把优先队列的 \(\log m\) 卡满,而且就算 \(m = n ^ 2\),\(\log m\) 和 \(\log n\) 也只差了一个 \(2\) 倍常数。这里给出线段树的参考代码,但是在 NKOJ(和其他任何 OJ)上不建议使用。
#include <cstdio>
#include <algorithm>
#include <cctype>
namespace fastio
{
const int MAXBUF = 1 << 20;
char buf[MAXBUF], *p1 = buf, *p2 = buf;
inline char getc() { return (p1 == p2) && (p2 = (p1 = buf) + fread(buf, 1, MAXBUF, stdin)), p1 == p2 ? EOF : *p1++; }
} // namespace fastio
using fastio::getc;
template <class _Tp>
inline _Tp& read(_Tp& x)
{
bool sign = 0;
char ch = getc();
for (; !isdigit(ch); ch = getc()) sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getc()) x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
const int maxn = 400000 + 10, maxm = 2000000 + 10;
struct graph
{
int cnt;
int st[maxm], to[maxm], last[maxn], next[maxm];
long long w[maxm];
graph() { cnt = 0; }
void add(int x, int y, long long z)
{
cnt++;
st[cnt] = x, to[cnt] = y, w[cnt] = z;
next[cnt] = last[x], last[x] = cnt;
}
}
g;
struct segmentTree
{
long long a[maxn];
struct node { int l, r, pos; } T[maxn << 2];
void build(int p, int l, int r)
{
T[p].l = l, T[p].r = r, T[p].pos = l;
if (l == r) a[l] = 1LL << 60;
else build(p << 1, l, (l + r) >> 1), build((p << 1) | 1, ((l + r) >> 1) + 1, r);
}
int modify(int p, int k, long long d)
{
if (T[p].r < k || T[p].l > k) return T[p].pos;
else if (T[p].l == k && T[p].r == k) return a[k] = d, T[p].pos = k;
else return T[p].pos = a[modify(p << 1, k, d)] <= a[modify((p << 1) | 1, k, d)] ? T[p << 1].pos : T[(p << 1) | 1].pos;
}
}
T;
long long dis[maxn];
long long dijk(int st, int ed, int n)
{
T.build(1, 1, n);
T.modify(1, st, 0);
for (int i = 1; i <= n; i++) dis[i] = 1LL << 60;
dis[st] = 0;
while (n--)
{
int u = T.T[1].pos;
if (T.a[u] >= 1LL << 60) break;
if (u == ed) return dis[u];
for (int j = g.last[u]; j != 0; j = g.next[j])
{
int v = g.to[j]; long long w = g.w[j];
if (dis[v] > dis[u] + w) T.modify(1, v, T.a[u] + w), dis[v] = dis[u] + w;
}
T.modify(1, u, 1LL << 60);
}
return -1;
}
int main()
{
int n, m;
read(n), read(m);
for (int i = 1; i <= m; i++)
{
int x, y;
long long z;
read(x), read(y), read(z);
g.add(x, y, z);
}
int st, ed;
read(st), read(ed);
printf("%lld", dijk(st, ed, n));
return 0;
}
Bellman-Ford
1. 朴素版
进行 \(n - 1\) 次遍历每个边的松弛操作。
因为在无负权回路图中最短路不会经过重复点,长度最多为 \(n - 1\),所以在第 \(i\) 次松弛操作中一定能松弛到最终答案的第 \(i\) 条边。
时间复杂度 \(O(n \times m)\)。如果题目限制最短路最多经过 \(t\) 条边,就是 \(O(t \times m)\)。
2. 队列优化(SPFA)
关于 SPFA,______。
显然只有最短路变化的点才可能更新其他点,所以每次可以把变化的点存下来,再用这些点去更新其他点。时间复杂度为边数乘每个点的平均入队次数 \(O(k \times m)\),随机图中 \(k < 5\),构造图可以卡到 \(O(n \times m)\)。有一些神奇的优化,但是肯定可以被卡。在负权图和一些特殊图中有一定的作用,但不多。
3. 判负权回路
如果进行 \(n - 1\) 次松弛操作后仍然可以松弛,那么图中存在负环。SPFA 中可以记录每个点的入队次数,超过 \(n\) 次说明存在负环。也可以记录到每个点的最短路经过的边数,超过 \(n-1\) 说明有负环。
Floyd-Warshall
1. 朴素版
设 \(f_{k,i,j}\) 表示 \(i\) 到 \(j\) 只经过前 \(k\) 个点的最短路。
则 \(f_{k,i,j} = \min(f_{k-1,i,j}, f_{k-1,i,k} + f_{k-1,k,j} )\)。
2. 滚动数组优化
滚动第一维,得到 \(f_{i,j} = \min(f_{i,k} + f_{k,j} )\)。
因为 \(k\) 并不在 \(i\) 到 \(k\) 的最短路中,所以 \(f_{i,k}\) 在此时表示 \(f_{k-1,i,k}\) 还是 \(f_{k,i,j}\) 都不会有影响,可以直接压缩。\(f_{k,j}\) 同理。
循环顺序保持不变,还是 \(k,i,j\)。
其实三个循环顺序可以随意交换,在外面再套一个 \(3\) 次的循环即可
没用的知识又增加了
3. 判负权回路
如果 \(f_{i,i} < 0\),说明点 \(i\) 在一个负权回路中。
4. 传递闭包
设 \(f_{i,j} = 1\) 表示 \(i\) 与 \(j\) 连通,反之不连通,然后使用 Floyd 的三层循环进行求解。
可以用 bitset 优化,时间复杂度 \(O(\frac{n ^ 3}{w})\)。
BFS
你就说能不能求最短路吧
边权为 \(1\) 用队列,边权为 \(0\) 或 \(1\) 用双端队列,如果经过一条边权为 \(0\) 的边更新一个点放到队头,边权为 \(1\) 放到队尾,第一次取出一个点时它的最短路就一定是已经确定的。时间复杂度 \(O(m)\)。
对于边权无限制,有两种解决办法。一是允许节点被多次更新 然后就变成 SPFA 了呢,二是改成优先队列 然后就变成 Dijkstra 了呢。
最短路树 / DAG 与最短路相关计数
在单源最短路中,连接每个点的前驱和它本身的边的集合是一个有根叶向树,称为最短路树,源点到某个节点的最短路就是树上根节点到这个点的距离。
因为最短路中不会出现环,且最短路的前缀一定是最短路,所以所有满足 \(dis_u + w(u, v) = dis_v\) 的边 \(u \to v\) 的集合是一个有向无环图,称为最短路 DAG。DAG 上的任何一条路径都是最短路。对最短路树计数相当于 DAG 生成树计数。同时,DAG 的拓扑序就是 \(dis\) 从小到大的顺序,也是 dijkstra 中节点的访问顺序,可以进行 DP。
对每一个点求出最短路 DAG 后枚举对每一条边答案的贡献(控制变量法——前物理科代表 \(a^6q^6\))。
#include <cstdio>
#include <algorithm>
const int maxn = 1500 + 10, maxm = 5000 + 10;
const long long inf = 1LL << 60;
struct graph
{
int cnt;
int st[maxm], to[maxm], last[maxn], next[maxm];
long long w[maxm];
graph() { cnt = 0; }
void add(int x, int y, long long z)
{
cnt++;
st[cnt] = x, to[cnt] = y, w[cnt] = z;
next[cnt] = last[x], last[x] = cnt;
}
}
g, gt;
struct segmentTree
{
long long a[maxn];
struct node { int l, r, pos; } T[maxn << 2];
void build(int p, int l, int r)
{
T[p].l = l, T[p].r = r, T[p].pos = l;
if (l == r) a[l] = inf;
else build(p << 1, l, (l + r) >> 1), build((p << 1) | 1, ((l + r) >> 1) + 1, r);
}
int modify(int p, int k, long long d)
{
if (T[p].r < k || T[p].l > k) return T[p].pos;
else if (T[p].l == k && T[p].r == k) return a[k] = d, T[p].pos = k;
else return T[p].pos = a[modify(p << 1, k, d)] <= a[modify((p << 1) | 1, k, d)] ? T[p << 1].pos : T[(p << 1) | 1].pos;
}
}
T;
long long dis[maxn];
int cnt = 0;
int ord[maxn];
void dijk(int st, int n)
{
cnt = 0;
T.build(1, 1, n);
T.modify(1, st, 0);
for (int i = 1; i <= n; i++) dis[i] = inf;
dis[st] = 0;
while (n--)
{
int u = T.T[1].pos;
if (T.a[u] >= inf) break;
ord[++cnt] = u;
for (int j = g.last[u]; j != 0; j = g.next[j])
{
int v = g.to[j]; long long w = g.w[j];
if (dis[v] > dis[u] + w) T.modify(1, v, T.a[u] + w), dis[v] = dis[u] + w;
}
T.modify(1, u, inf);
}
return;
}
const long long mod = 1e9 + 7;
long long ans[maxm];
long long in[maxn], out[maxn];
int main()
{
int n, m;
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++)
{
int x, y;
long long z;
scanf("%d %d %lld", &x, &y, &z);
g.add(x, y, z);
gt.add(y, x, z);
}
for (int i = 1; i <= n; i++)
{
dijk(i, n);
for (int j = 1; j <= n; j++) in[j] = out[j] = 0;
in[i] = 1;
for (int k = 1; k <= cnt; k++)
{
int u = ord[k];
for (int j = gt.last[u]; j != 0; j = gt.next[j])
{
int v = gt.to[j];
long long w = gt.w[j];
if (dis[v] + w == dis[u]) in[u] = (in[v] + in[u]) % mod;
}
}
for (int k = cnt; k >= 1; k--)
{
int u = ord[k];
out[u] = 1;
for (int j = g.last[u]; j != 0; j = g.next[j])
{
int v = g.to[j];
long long w = g.w[j];
if (dis[u] + w == dis[v]) out[u] = (out[u] + out[v]) % mod;
}
}
for (int j = 1; j <= m; j++)
{
int u = g.st[j], v = g.to[j];
if (dis[u] + g.w[j] == dis[v]) ans[j] = (ans[j] + in[u] * out[v]) % mod;
}
}
for (int i = 1; i <= m; i++) printf("%lld\n", ans[i]);
return 0;
}
最小环
第一种方法是枚举图中每一条边,再用 Dijkstra 计算这条边的两个端点在不经过这条边本身时的最短路,最终答案即为 \(dis_{v,u} + w_{u,v}\)。时间复杂度为 \(O(m ^ 2 \times \log m)\)。
第二种方法需要用到 Floyd 中的性质。在进行第 \(k\) 次最外层循环前假定最小环中编号最大的点为 \(k\),然后枚举与 \(k\) 直接相邻且编号比它小的的两个点 \(u,v\),此时 \(dis_{v,u}\) 表示 \(v\) 在经过所有编号小于 \(k\) 的节点到 \(u\) 的最短路,最小环长度即为 \(dis_{v,u} + w_{u,k} + w_{k,v}\)。显然可以枚举到每一个最小环。时间复杂度同 Floyd \(O(n^3)\)。
连通性 / 传递性
考虑并查集。如果是删边操作,可以离线后倒序处理。
虚点
通过人为构造一些虚点使得边数更少。常用的套路有为每一层建立一个入点和一个出点。
例题参考博客 虚点/虚边专题 - TieT - 博客园。
分层图最短路 / 多维最短路 / 拆点
其实就是 DP 思想,通过增加状态来方便转移。
补图
补图中的边数可以达到 \(n^2\) 级别,一般情况下绝对无法直接求解,因此一般有一个限制,就是在通过补图遍历到一个点时,这个点的最短路就已经确定了,比如图中所有边权为 \(1\)。
在 BFS 或 Dijkstra 过程中用一个有序链表(或 std::set)维护当前所有未被访问的点集合(即 T 集合),同时以有序邻接表存图。每次用双指针遍历邻接表和链表,如果邻接表中没有出现且链表中出现,就更新最短路,这个点的最短路就是确定的,并在 T 集合中删除。
时间复杂度均摊分析,\(O(n+m)\)。
//HDU5876
#include <cstdio>
#include <algorithm>
#include <queue>
#include <vector>
#include <list>
const int maxn = 2e5 + 10, maxm = 2e5 + 10;
std::vector<int> g[maxn];
std::list<int> s;
std::queue<int> q;
int dis[maxn], mark[maxn];
void dijk(int st, int n)
{
for (int i = 1; i <= n; i++) dis[i] = 1e9, mark[i] = 0;
s.clear();
for (int i = 1; i <= n; i++) if (i != st) s.push_back(i);
dis[st] = 0;
q.push(st);
while (!q.empty())
{
int u = q.front();
q.pop();
if (mark[u]) continue;
mark[u] = 1;
auto i = g[u].begin();
auto j = s.begin();
while (i != g[u].end() && j != s.end())
{
int v = *j;
if (*i == v) i++, j++;
else if (*i < v) i++;
else
{
dis[v] = dis[u] + 1;
q.push(v);
j = s.erase(j);
}
}
}
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
int n, m;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) g[i].clear();
for (int i = 1; i <= m; i++)
{
int x, y;
scanf("%d %d", &x, &y);
g[x].push_back(y);
g[y].push_back(x);
}
for (int i = 1; i <= n; i++) std::sort(g[i].begin(), g[i].end()), g[i].push_back(n + 1);
int st;
scanf("%d", &st);
dijk(st, n);
for (int i = 1; i <= n; i++)
{
if (i == st) continue;
printf("%d ", dis[i] > 1e8 ? -1 : dis[i]);
}
printf("\n");
}
return 0;
}
二进制分组处理多源同汇最短路
有向图中有一些标记点,求起点终点不同且都为标记点的最短路。
遍历所有标记点的编号的每个二进制位,每次按每个标记点这一位的二进制为 \(0\) 或 \(1\) 分为起点集合和终点集合跑最短路,可以证明对于每一对标记点都会至少一次分别分到两个集合中,时间复杂度 \(O(m \times \log^2 n)\)。
也可以记录每个点从两个不同标记点到达它的最短路,时间复杂度 \(O(m \times \log n)\)。
Bellman-Ford 处理负权回路
SPFA + swap 把 NKOJ 的数据水过了,但 UVA 原题过不了。
正解是在 Bellman-Ford 过程中记录每个节点在最短路上的前驱节点,如果从一个点开始可以从它的前驱所指向的路径返回它自己,说明这个点在负权回路上。然后在这个负权回路中寻找最早到达时间最小的节点更新这个负环其他节点的最短路。重复执行直到所有点的最短路都无法被更新。
Dijkstra 处理后效性期望 DP
\(f_u\) 表示从 \(u\) 点到达终点的期望购票数。
至于为什么期望 DP 一般倒推,是因为从一个点转移到其它点的概率是确定的,而从其它点转移到这个点的概率不一定确定,所以一般期望 DP 倒推会更方便。可以参考 浅谈期望 DP 的转移问题 - Retired_Doubeecat - 洛谷博客。
不难发现如果在点 \(u\) 抽到了去点 \(v\) 的票,且 \(f_v \ge f_u\),最佳策略是留在原地。反之,如果 \(f_v < f_u\),留在点 \(u\) 的期望依然是 \(f_u\),不如去点 \(v\)。
换句话说,每条无向边最终的实际指向都是由 \(f\) 较大的指向 \(f\) 较小的,构成一个有向无环图。
进而可以得到转移方程:
相当优美。但是我们发现计算 \(f_u\) 时依然需要 \(f_u\) 的值,无法转移。
所以使用 Dijkstra 的思想。当前未确定的点中期望最小的点已经无法被其它点更新。
然后就可以快乐地推式子了。
维护 \(cnt_v\) 表示 \(v \to u\) 且 \(f_u < f_v\) 的个数,\(sum_v\) 表示 \(v \to u\) 且 \(f_u < f_v\) 的 \(f_u\) 的和。
每次找出当前期望最小的点 \(u\),遍历所有 \(v \to u\),且 \(f_v > f_u\)。更新 \(sum_v\) 和 \(cnt_v\),并重新计算 \(f_v\)。
更加优美。比某些人动态维护 f 的做法好看多了。
无向正权图删边最短路
人类智慧。
删边最短路问题 - dengyaotriangle - 洛谷博客
线段树优化建图
「算法笔记」线段树优化建图 - maoyiting - 博客园(参考资料 + 图片来源)
通过类似线段树的结构,建立两棵二叉树,将二叉树上的每一个节点表示一个区间,将单点和区间之间连边的边数降为最多 \(2 \times \log n\)。某种意义上算是虚点优化建图的加强版。
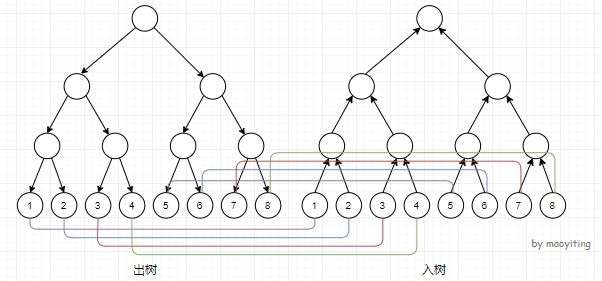
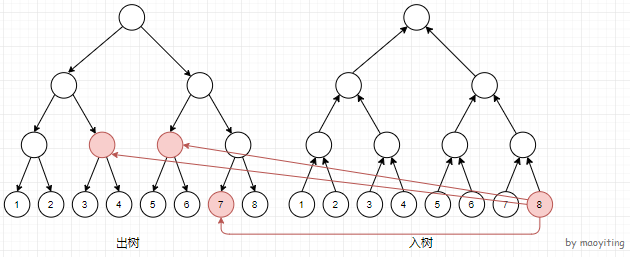
结合图片还是很好理解的。
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
const int maxn = 1e5 + 10;
const int maxm = maxn * 10 + maxn * 2 * (int)log2(maxn);
struct graph { int cnt; graph() { cnt = 0; } int st[maxm], to[maxm], last[maxn * 8], next[maxm]; long long w[maxm]; void add(int x, int y, long long z) { cnt++, st[cnt] = x, to[cnt] = y, w[cnt] = z, next[cnt] = last[x], last[x] = cnt; } } g;
struct segmentTree
{
int n;
int pos[maxn];
struct node { int l, r; } T[maxn * 8];
void build(int p, int l, int r)
{
T[p].l = l, T[p].r = r, T[p + 4 * n].l = l, T[p + 4 * n].r = r;
if (l == r) pos[l] = p, g.add(p, p + 4 * n, 0), g.add(p + 4 * n, p, 0);
else
{
build(2 * p, l, (l + r) / 2), build(2 * p + 1, (l + r) / 2 + 1, r);
g.add(p, 2 * p, 0), g.add(p, 2 * p + 1, 0);
g.add(2 * p + 4 * n, p + 4 * n, 0), g.add(2 * p + 1 + 4 * n, p + 4 * n, 0);
}
}
void add(int p, int k, int l, int r, long long w, int opt) //opt = 1 ? k -> [l,r] : [l,r] -> k
{
if (T[p].l > r || T[p].r < l || T[p].l > T[p].r) return;
else if (l <= T[p].l && T[p].r <= r) g.add(opt == 1 ? pos[k] + 4 * n : p + 4 * n, opt == 1 ? p : pos[k], w);
else add(2 * p, k, l, r, w, opt), add(2 * p + 1, k, l, r, w, opt);
}
}
T;
long long dis[maxn * 8]; bool mark[maxn * 8]; void dijkstra(int st, int n) { for (int i = 1; i <= n; i++) dis[i] = 1LL << 60, mark[i] = 0; dis[st] = 0; std::priority_queue< std::pair<long long, int> > q; q.push(std::make_pair(0, st)); while (!q.empty()) { int u = q.top().second; q.pop(); if (mark[u]) continue; mark[u] = 1; for (int j = g.last[u]; j != 0; j = g.next[j]) { int v = g.to[j]; long long w = g.w[j]; if (dis[v] > dis[u] + w) dis[v] = dis[u] + w, q.push(std::make_pair(-dis[v], v)); } } return; }
int main()
{
int n, q, s;
scanf("%d %d %d", &n, &q, &s);
T.n = n;
T.build(1, 1, n);
for (int i = 1; i <= q; i++)
{
int opt;
scanf("%d", &opt);
if (opt == 1)
{
int u, v;
long long w;
scanf("%d %d %lld", &u, &v, &w);
g.add(T.pos[u] + 4 * n, T.pos[v], w);
}
else
{
int k, l, r;
long long w;
scanf("%d %d %d %lld", &k, &l, &r, &w);
T.add(1, k, l, r, w, opt - 1);
}
}
dijkstra(T.pos[s] + 4 * n, 8 * n);
for (int i = 1; i <= n; i++) printf("%lld ", dis[T.pos[i]] >= 1LL << 59 ? -1 : dis[T.pos[i]]);
return 0;
}
其实还可以 ST 表优化建图,分块优化建图等。
参考:各种优化建图 - Alex_Wei - 博客园,常见优化建图技巧 - panyf - 洛谷博客,DS 优化建图 - _lgswdn - 洛谷博客。
另外几道跟最短路有一定关系(但不多)的杂题。
[CSP-S 2022] 假期计划
看到范围 \(n \le 2500\) 不难想到可以枚举其中两个点。既然都直接枚举了,肯定要枚举带来最多信息的两个点,以便 \(O(1)\) 计算答案。所以先预处理每个点和 1 点可以共同到达的点并按分数排序,再枚举 B,C 两个点,并在 B 和 1 可以共同到达的前 \(3\) 个顶点中枚举 A,在 C 和 1 可以共同到达的前 \(3\) 个顶点中枚举 D,然后判断四个点是否相同,不同则更新答案。可以证明,这样一定能找到最优解。
NKOJ8736 指针分析
用整形压位记录每一个全局指针和每一个对象的每一个指针可以访问到的对象,每次操作或一下即可。
为了处理任意顺序,使用 Bellman-Ford 的思想,反复依次执行操作,直到无法更新。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号