【求最近公共祖先LCA】Nearest Common Ancestors

Nearest Common Ancestors
Time Limit: 1000MS   Memory Limit: 10000K
Total Submissions: 21782   Accepted: 11412

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
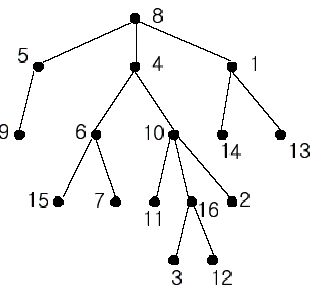
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

题意：给你一棵树，然后输入两个点，让你求出这两个点的最近公共祖先;

解法：简单的LCA；

代码：2015.8.12

 1 #include<iostream>
 2 #include<stdio.h>
 3 #include<algorithm>
 4 #include <string.h>
 5 #define MAX 10010
 6 #define MM 10010
 7 using namespace std;
 8 int InD[MAX];
 9 int fa[MAX];/*记录父节点*/
10 struct edge{int to,next,v;}edg[MAX*2],omg[MM*2];
11 int ans[MAX][3];
12 int first[MAX];/*图的节点*/
13 int first_s[MAX];/*询问的节点*/
14 int sign;
15 bool Vis[MAX];/*点标记*/
16 void Cread(int N)/*初始化*/
17 {
18     for(int i=0;i<=N;i++)
19     {
20         first[i]=first_s[i]=InD[i]=0;
21         Vis[i]=true;
22         fa[i]=i;
23     }sign=1;
24 }
25 int Find(int x)/*寻找父亲节点*/
26 {
27     if(x!=fa[x])fa[x]=Find(fa[x]);
28     return fa[x];
29 }
30 
31 void add_e(int x,int y)/*添加图的边*/
32 {
33     edg[sign].to=y;
34     edg[sign].next=first[x];
35     first[x]=sign++;
36 }
37 
38 void add_o(int x,int y,int z)/*添加查询的边*/
39 {
40     omg[sign].to=y;
41     omg[sign].v=z;
42     omg[sign].next=first_s[x];
43     first_s[x]=sign++;
44 }
45 
46 void Tarjan_LCA(int n)
47 {
48     Vis[n]=false;
49     fa[n]=n;
50     for(int i=first_s[n];i;i=omg[i].next)
51     {
52         int TMD=omg[i].to;
53         if(!Vis[TMD])/*访问被标记过的询问的连接点*/
54         {
55             ans[omg[i].v][2]=Find(TMD);
56         }
57     }
58     for(int i=first[n];i;i=edg[i].next)
59     {
60         int TMD=edg[i].to;
61         if(Vis[TMD])/*访问还没有被标记过的点*/
62         {
63             Tarjan_LCA(TMD);
64             fa[TMD]=n;
65         }
66     }
67 }
68 int main()
69 {
70     int T,n,m,k,i,j,a,b,c,A,B;
71     scanf("%d",&T);
72     while(T--)
73     {
74         scanf("%d",&n);m=1;/*m为询问次数*/
75         Cread(n);/*初始化*/
76         for(i=1;i<n;i++)
77         {
78             scanf("%d%d",&a,&b);InD[b]++;
79             add_e(a,b);add_e(b,a);
80         }
81         for(i=1,sign=1;i<=m;i++)
82         {
83             scanf("%d %d",&a,&b);
84             add_o(a,b,i);add_o(b,a,i);
85             ans[i][0]=a;ans[i][1]=b;
86         }
87         for(i=1;i<=n;i++)
88             if(!InD[i]){Tarjan_LCA(i);break;}/*树形图，所以任意一点可作为根基点，与相对距离无关*/
89         for(i=1;i<=m;i++)/*输出每次询问的答案*/
90             printf("%d\n",ans[i][2]);/*输出两点之间的距离*/
91     }
92     return 0;
93 }
View Code

 

posted @ 2015-08-12 00:16  Wurq  阅读(194)  评论(0)    收藏  举报