数列的考查角度收集整理1[三轮总结]

数列性质

考查数列的通项公式或数列的函数性质

1、给定数列的前有限项，求数列$\{a_n\}$的通项公式(常以选择填空题形式考查)

数列$\cfrac{15}{2}$，$\cfrac{24}{5}$，$\cfrac{35}{10}$，$\cfrac{48}{17}$，$\cfrac{63}{26}$，$\cdots$的一个通项公式为$a_n$=______；

提示：$a_n=\cfrac{(n+3)^2-1}{n^2+1}$；

解后反思：观察归纳法，突破这类题目的技巧在于，熟练记忆常见数列的通项公式，然后组合即可。

强烈建议熟练记忆

2、考查数列的周期性

已知数列$\{a_n\}$满足$a_{n+2}=a_{n+1}-a_n$，且$a_1=2，a_2=3$，则$a_{2016}$的值为（）。

法1：利用递推关系推导出数列的前有限项，周期自然就知道了。

由题目可知$a_1=2，a_2=3，a_3=a_2-a_1=1，a_4=a_3-a_2=-2$，

$a_5=a_4-a_3=-3，a_6=a_5-a_4=-1，a_7=a_6-a_5=2$，

即$a_7=a_1$，周期$T=6$，所以$a_{2016}=a_6=-1$

法2：由$a_{n+2}=a_{n+1}-a_n$可得到$a_{n+3}=a_{n+2}-a_{n+1}$，

两个式子相加，得到$a_{n+3}=-a_n$，

仿上可得$a_{n+6}=a_{[(n+3)+3]}=-a_{n+3}=-(-a_n)=a_n$，

故周期$T=6$，其余仿上完成。

已知数列$\{a_n\}$满足$a_{n+1}a_{n-1}=a_n(n\ge 2)$，且$a_1=1，a_2=3$，则$a_{2016}$的值为（）

法1：利用递推关系推导出数列的前有限项，$a_1=1$，$a_2=3$，$a_3=\cfrac{a_2}{a_1}=3$，$a_4=\cfrac{a_3}{a_2}=1$，

$a_5=\cfrac{a_4}{a_3}=\cfrac{1}{3}$，$a_6=\cfrac{a_5}{a_4}=\cfrac{1}{3}$，$a_7=\cfrac{a_6}{a_5}=1$，

周期$T=6$，所以$a_{2016}=a_6=\cfrac{1}{3}$.

法2：由$a_{n+1}=\cfrac{a_n}{a_{n-1}}$可得，$a_{n+2}=\cfrac{a_{n+1}}{a_n}$，

两式相乘得到$a_{n+2}=\cfrac{1}{a_{n-1}}$，即$a_{n+3}=\cfrac{1}{a_n}$，

$a_{n+6}=a_{[(n+3)+3]}=\cfrac{1}{a_{n+3}}=a_n$，

故周期$T=6$，其余仿上完成。

(全国大联考，2016第三次联考第10题)设数列$\{a_n\}$前$n$项和为$S_n$，$a_{203}-a_{204}=a_{202}=1$，且$a_n+a_{n+1}+a_{n+2}=4$，则$S_{200}$等于多少？

分析：本题目考查数列的单调性，由$a_n+a_{n+1}+a_{n+2}=4$，

得到$a_{n+1}+a_{n+2}+a_{n+3}=4$，两式相减得到，$a_{n+3}=a_n$，故$T=3$，

又由$a_{202}+a_{203}+a_{204}=4$，$a_{202}=1$，及$a_{203}-a_{204}=1$，得到$a_{203}=2$，

又$a_{202}=1$，故$a_{201}=1$，$a_{200}=2$，$a_{199}=1$，又$200=66\times 3+2$，

则有$S_{200}=66(a_1+a_2+a_3)+a_{199}+a_{200}=66\times 4+2+1=267$。

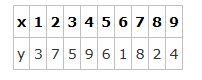
(2016.西安质检改编)对于函数$y=f(x)$部分$x$与$y$的对应关系如下表：

数列$\{x_n\}$满足：$x_1=1$，且对于任意的$n\in N_*$，点$(x_n，x_{n+1})$都在函数$y=f(x)$的图像上，则$x_1+x_2+\cdots+x_{2018}$=_________。

分析：这是一个很新颖的数列题目，但是和函数的列表法紧密结合，要顺利解答还需要一定的数学素养。

由题目可知$y=f(x)，x_{n+1}=f(x_n)，x_1=1$，

则有$x_2=f(x_1)=f(1)=3$；$x_3=f(x_2)=f(3)=5$；

$x_4=f(x_3)=f(5)=6$；$x_5=f(x_4)=f(6)=1$；

$\cdots，T=4$；

$\sum\limits_{k=1}^{2018}{x_k}=504(x_1+x_2+x_3+x_4)+(x_1+x_2)=504\times 15+4=7564$

解后反思：由于数列也是函数，所以数列的周期性的考查和其他函数的周期性的考查是一样的，建议你看看这篇博文。

数列的周期性

3、考查数列的单调性

已知$a>0$，数列$\{a_n\}$满足$a_n = \begin{cases} (3-a)n-3，n\leq 7 \\ a^{n-6} ，n>7 \end{cases}$，数列$\{a_n\}$是单调递增数列，求$a$的取值范围。

分析：由题目可知，$\begin{cases} 3-a >0 \\ a >1 \\ (3-a)7-3< a^{8-6}\end{cases}$

解得：$a \in(2，3)$；

备注：既要保证每段上的单调性，还要保证转折点处的单调性。

已知$a>0$，函数$f(x)$满足$f(x)=\begin{cases} (3-a)x-3 &x\leq 7 \\ a^{x-6} &x>7 \end{cases}$，函数$f(x)$在$R$上单调递增，求$a$的取值范围。

分析：由题目可知，$\begin{cases} &3-a >0 \\ &a>1 \\ &(3-a)7-3\leq a^{7-6}\end{cases}$；

即就是$\begin{cases}&a<3 \\ &a>1 \\ &a\ge \cfrac{9}{4}\end{cases}$

解得：$a\in[\cfrac{9}{4}，3)$；

备注：既要保证每段上的单调性，还要保证转折点处的单调性。

解后反思：强烈建议你看看这篇博文，数列是特殊的函数

4、考查数列的最值

已知数列$\{a_n\}$满足 $a_{n+1}=a_n+2n$，且$a_1=33$，则$\cfrac{a_n}{n}$的最小值为【】

$A.21$ $B.10$ $C.\cfrac{21}{2}$ $D.\cfrac{17}{2}$

分析：选$C$。由已知条件可知，当$n\ge 2$ 时，

$a_n=a_1+(a_2-a_1)+(a_3-a_2)+\cdots+(a_n-a_{n-1})=33+2+4+…+2(n-1)$

$=n^2-n+33$，又$n=1$时，$a_1=33$，满足此式。所以$\cfrac{a_n}{n} =n+\cfrac{33}{n}-1$

令$f(n)=\cfrac{a_n}{n}=n+\cfrac{33}{n}-1$，则$f(n)$在$[1，5]$上为减函数，

在$[6,+\infty)$上为增函数，又$f(5)=\cfrac{53}{5}$，$f(6)=\cfrac{21}{2}$，则$f(5)>f(6)$，

故$f(n)=\cfrac{a_n}{n}$的最小值为$\cfrac{21}{2}$。故选$C$。

已知等差数列$\{a_n\}$的前$n$项和为$S_n$，且有$a_1=7$，公差为$d$，当且仅当$n=8$时$S_n$取到最大值，求$d$的取值范围。

分析：由题意可知，$n=8$时$S_n$取到最大值，

则必有$\begin{cases}d<0\\a_8>0\\a_9<0\end{cases}$，

即$\begin{cases}d<0\\7+7d>0\\7+8d<0\end{cases}$，

解得$-1< d <-\cfrac{7}{8}$。

解后反思：

1、强烈建议你看看这篇博文，等差数列的$S_n$的最值

2、等差数列$a_n=f(n)$和$S_n=g(n)$的[图像]

(2016新课标1卷第15题)设等比数列$\{a_n\}$满足$a_1+a_3=10$，$a_2+a_4=5$，则$T_n=a_1\cdot a_2\cdot a_3\cdots a_n$的最大值是多少？

法1：函数法，容易求得$a_1=8，q=\cfrac{1}{2}$，则$a_n=8\cdot(\cfrac{1}{2})^{n-1}$；

故$T_n=a_1\cdot a_2\cdot a_3\cdots a_n$

$=8^n\cdot (\cfrac{1}{2})^{\cfrac{n(n-1)}{2}}$

$=2^{\cfrac{-n^2+7n}{2}}$

$=2^{\cfrac{-(n-\cfrac{7}{2})^2+\cfrac{49}{4}}{2}}$，

故当$n=3或4$时，$T_n$有最大值，$(T_n)_{max}=2^6=64$；

法2：仿上法2，使得$T_n$取得最大值时，必有$a_n\ge 1$，

由此得到$n\leq 4$。

计算得到$a_1=8$，$a_2=4$，$a_3=2$，$a_4=1$，$a_5=\cfrac{1}{2}$，

故$T_n\leq T_4=a_1a_2a_3a_4=64$；

已知$S_n$是等比数列$\{a_n\}$的前$n$项和，$a_1=30$，$8S_6=9S_3$，设$T_n=a_1\cdot a_2\cdot a_3\cdots a_n$，则使$T_n$取得最大值的$n$为多少？

法1：函数法，$a_1=30$，由$8S_6=9S_3$得到$q=\cfrac{1}{2}$，

故$a_n=30\cdot(\cfrac{1}{2})^{n-1}$，

$T_n=a_1\cdot a_2\cdots a_n$

$=30\cdot[30\cdot(\cfrac{1}{2})]\cdots [30\cdot(\cfrac{1}{2})^{n-1}]$

$=30^n\cdot (\cfrac{1}{2})^{1+2+\cdots+(n-1)}$

$=30^n\cdot (\cfrac{1}{2})^{\cfrac{n(n-1)}{2}}$，题目到此，思路受阻。

法2：$a_1=30$，由$8S_6=9S_3$得到$q=\cfrac{1}{2}$，

故$a_n=30\cdot(\cfrac{1}{2})^{n-1}$，

由于$T_n$为乘积式，故使得$T_n$取得最大值时，必有$a_n\ge 1$，

由此得到$n\leq 5$。故$n_{max}=5$。

数学常识

1、等差数列中由$a_n$的正负确定数列前$n$项之和$S_n$的最值：

当$a_1<0，d>0$时，所有负项之和最小；当$a_1>0，d<0$时，所有正项之和最大；

2、正项等比数列中由$a_n$的值的范围，确定数列前$n$项之积$T_n$的最值：当$a_n\ge 1$时，$T_n$最大；

3、求$S_n$的最值时，分界为0；求$T_n$的最值时，分界为1；作差法与0做大小比较，作商法与1做大小比较。

5、借助充要条件考查数列

(2017兰州模拟)在等比数列$\{a_n\}$中，$a_1 < a_2 < a_3$是等比数列$\{a_n\}$单调递增的()条件。

$A.充分不必要$ $B.必要不充分$ $C.充分必要$ $D.既不充分也不必要$

分析：当$a_1 < a_2 < a_3$时，设公比为$q$，则有$a_1 < a_1q < a_1q^2$；

若$a_1>0$，则有$1< q< q^2$，得到$q >1$，

此时$a_n=a_1\cdot q^{n-1}$，指数型函数，单调递增；

若$a_1<0$，则有$1> q > q^2$，得到$0< q <1$，

此时$a_n=a_1\cdot q^{n-1}$，指数型函数，单调递增；

反之，当数列$\{a_n\}$是递增等比数列，必有$a_1 < a_2< a_3$，

故选 C、充分必要条件。

反思：由等比数列的通项公式可知，$a_n=a_1\cdot q^{n-1}$可知，

当$a_1 >0且q >1$或者$a_1 <0且0< q <1$时，$a_n$单调递增；

当$a_1 <0且q>1$或者$a_1 >0且0< q <1$时，$a_n$单调递减；

当$q=1$时为常数列，无单调性；

当$q <0$时为摆动数列，无单调性。

在等比数列$\{a_n\}$中，$q>1$是等比数列$\{a_n\}$单调递增的()条件。

$A.充分不必要$ $B.必要不充分$ $C.充分必要$ $D.既不充分也不必要$

分析：由上述分析可知：$a_n=a_1\cdot q^{n-1}$，指数型函数，

它的变化取决于两个要素，$a_1$和$q$，故选D。

在等差数列$\{a_n\}$中，$d>0$是等差数列$\{a_n\}$单调递增的()条件。

$A.充分不必要$ $B.必要不充分$ $C.充分必要$ $D.既不充分也不必要$

分析：由$a_n=dn+(a_1-d)$可知，选C。

解后反思：(数学常识)

$b=\sqrt{ac}$，是$a、b、c$成等比数列的既不充分也不必要条件；

$b=\sqrt{ac}(ac>0)$，是$a、b、c$成等比数列的充分不必要条件；

$b=\pm \sqrt{ac}$，是$a、b、c$成等比数列的必要不充分条件；

$b=\pm \sqrt{ac}(ac>0)$，是$a、b、c$成等比数列的充分必要条件；

$a_{n+1}=2a_n(n\in N^*)$是$\cfrac{a_{n+1}}{a_n}=2$(或者数列$\{a_n\}$为等比数列)的必要不充分条件。

6、借助切线考查数列

【2016•德州模拟】函数$y＝x^2(x>0)$的图像在点$(a_k，a_k^2)$处的切线与$x$轴交点的横坐标为$a_{k+1}$，

其中 $k\in N*$，若$a_1＝16$，则$a_1＋a_3＋a_5$的值是________．

分析：由$f'(x)=2x$得，在点$(a_k，a_k^2)$处的切线方程为$y-a_k^2=2a_k(x-a_k)(k\in N*)$，

令$y=0$，得到切线方程与$x$轴的交点的横坐标为$x=\cfrac{a_k}{2}$，

即$a_{k+1}=\cfrac{a_k}{2}$，即$\cfrac{a_{k+1}}{a_k}=\cfrac{1}{2}$，

故数列$\{a_k\}$是首项为$a_1=16$，公比为$\cfrac{1}{2}$的等比数列，

故$a_1＋a_3＋a_5=16+16\cdot (\cfrac{1}{2})^2+16\cdot (\cfrac{1}{2})^4=21$。

总结：1、求在点处的切线方程；2、等比数列

对正整数$n$，设曲线$y=(2-x)x^n$在$x=3$处的切线与$y$轴交点的纵坐标为$a_n$，则数列$\{\cfrac{a_n}{n+2}\}$的前$n$项和为________。

分析：由于$y=(2-x)x^n$，则$y'=-x^n+n(2-x)x^{n-1}$；

则$y'|_{x=3}=-3^n-n3^{n-1}=-3^{n-1}(n+3)$；

故切线方程为$y+3^n=-3^{n-1}(n+3)(x-3)$，

令$x=0$，得到切线与$y$轴的交点的纵坐标为$a_n=(n+2)3^n$，

故$\cfrac{a_n}{n+2}=3^n$，为等比数列，

故数列$\{\cfrac{a_n}{n+2}\}$的前$n$项和为$S_n=\cfrac{3(1-3^n)}{1-3}=\cfrac{3^{n+1}-3}{2}$。

posted @ 2018-04-15 20:53 静雅斋数学阅读(541) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

数列的考查角度收集整理1[三轮总结]

相关运算

数列性质

公告