正余弦定理解三角形习题

前言

常用结论

• 以下为三角形中的常用结论，

①\(A+B=\pi-C\)，\(\cfrac{A+B}{2}=\cfrac{\pi}{2}-\cfrac{C}{2}\)；

②在三角形中，大角对大边，大边对大角；

③任意两边之和大于第三边，任意两边之差小于第三边；

④在\(\triangle ABC\)中，\(\tan A+\tan B+\tan C=\tan A\cdot\tan B\cdot\tan C\)，\((A，B，C\neq \cfrac{\pi}{2})\)；

典例剖析

【2015高考新课标2高考真题第17题】\(\Delta ABC\)中，\(D\)是\(BC\)上的点，\(AD\)平分\(\angle BAC\)，\(\Delta ABD\)的面积是\(\Delta ADC\)面积的\(2\)倍。

(1)、求\(\cfrac{sinB}{sinC}\)；

(2)、若\(AD=1\)，\(DC=\cfrac{\sqrt{2}}{2}\)，求\(BD\)和\(AC\)的长。

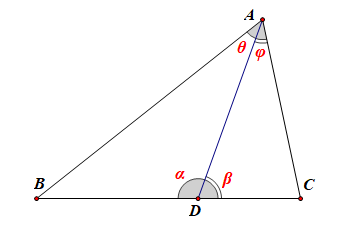
分析：(1) 先转化\(\cfrac{sinB}{sinC}=\cfrac{b}{c}\)；接下来只需要在\(\Delta ABC\)中利用某个条件，求得\(\cfrac{b}{c}\)即可；

由于\(\cfrac{S_{\Delta ABD}}{S_{\Delta ACD}}=\cfrac{\cfrac{1}{2}\cdot AB\cdot AD\cdot sin\angle BAD }{\cfrac{1}{2}\cdot AC\cdot AD\cdot sin\angle CAD }\)

\(=\cfrac{\cfrac{1}{2}\cdot AB\cdot AD\cdot sin\theta }{\cfrac{1}{2}\cdot AC\cdot AD\cdot sin\phi }=\cfrac{AB}{AC}=\cfrac{c}{b}=2\)

故\(\cfrac{sinB}{sinC}=\cfrac{b}{c}=\cfrac{1}{2}\)；

(2)、由\(\cfrac{S_{\Delta ABD}}{S_{\Delta ACD}}=\cfrac{\cfrac{1}{2}\cdot BD\cdot h}{\cfrac{1}{2}\cdot CD\cdot h}=2\)

则有\(\cfrac{BD}{CD}=2\)，又\(DC=\cfrac{\sqrt{2}}{2}\)，则\(BD=\sqrt{2}\)。

在\(\Delta ABD\)中，由余弦定理可知，\(AB^2=AD^2+BD^2-2\cdot AD\cdot BD\cdot cos\alpha①\)，

在\(\Delta ACD\)中，由余弦定理可知，\(AC^2=AD^2+CD^2-2\cdot AD\cdot CD\cdot cos\beta②\)，

由\(①+2\times ②\)得到，\(AB^2+2AC^2=3AD^2+BD^2+2CD^2=6\)，又\(AB=2AC\)

解得\(AC=1\)。

【解后反思】①、看到三角形面积，则应该想起\(S_{\Delta}=\cfrac{1}{2}absinC=\cfrac{1}{2}a\cdot h_{a}\)；

②、求\(BD\)长，思路一是利用面积的方法，思路二还可以用角平分线定理，

由\(\cfrac{AB}{AC}=\cfrac{BD}{DC}\)，又\(\cfrac{c}{b}=\cfrac{AB}{AC}=2\)，故\(\cfrac{BD}{DC}=2\)，即\(BD=2CD=\sqrt{2}\)。

③、本题的关键题眼

第一问中，\(\theta=\phi\)，故面积中\(sin\theta=sin\phi\)

第二问中求\(BD\)的长，既可以利用面积之比，也可以利用角平分线定理；

第二问中求\(AC\)的长，既可以利用\(cos\theta=cos\phi\)得到相等关系，也可以利用\(cos\alpha+cos\beta=0\)得到相等关系；

【2016山东高考】已知在\(\Delta ABC\)中，角\(A，B，C\)的对边分别是\(a，b，c\)，已知\(b＝c\)，\(a^2＝2b^2(1－sin A)\)，则 \(A=\) 【 】

$A、\cfrac{3\pi}{4}$ $B、\cfrac{\pi}{3}$ $C、\cfrac{\pi}{4}$ $D、\cfrac{\pi}{6}$

法1：由\(a^2=b^2+c^2-2bccosA\)及\(a^2＝2b^2(1－sin A)\)， 且有 \(b＝c\)，

\(2b^2(1－sin A)=2b^2-2b^2cosA=2b^2(1-cosA)\)，

即\(1-sinA=1-cosA\)，则有\(tanA=1\)，故\(A=\cfrac{\pi}{4}\)，选\(C\)。

法2：由题目\(B=C，A+B+C=\pi\)，可知\(B=\cfrac{\pi}{2}-\cfrac{A}{2}\)，

由正弦定理及\(a^2＝2b^2(1－sin A)\)可得，

\(sin^2A=2sin^2B(1-sinA)\)，即\(sin^2A=2sin^2(\cfrac{\pi}{2}-\cfrac{A}{2})(1-sinA)\)，

即\(sin^2A=2cos^2\cfrac{A}{2}\cdot (1-sinA)\)，即\(4sin^2\cfrac{A}{2}\cdot cos^2\cfrac{A}{2}=2cos^2\cfrac{A}{2}\cdot (1-sinA)\)，

即\(cos^2\cfrac{A}{2}\cdot (1-sinA-2sin^2\cfrac{A}{2})=0\)

即\(cos^2\cfrac{A}{2}\cdot (cosA-sinA)=0\)

由于\(A\in (0，\pi)\)，\(\cfrac{A}{2}\in(0，\cfrac{\pi}{2})\)，\(cos\cfrac{A}{2}\neq 0\)

故\(cosA=sinA\)，\(tanA=1\)，则\(A=\cfrac{\pi}{4}\)。选\(C\)。

【2016天津高考】在\(\Delta ABC\)中，\(AB=\sqrt{13}\)，\(BC=3\)，\(\angle C=120^{\circ}\)，则\(AC\)=【】

$A、1$ $B、2$ $C、3$ $D、4$

分析：本题目已知\(c=AB=\sqrt{13}\)，\(a=BC=3\)，\(\angle C=120^{\circ}\)，

即已知两边及一边的对角，求第三边\(AC=b=?\)；

求解思路可以用正弦定理，也可以用余弦定理，不过使用余弦定理一次就能到位。

由\(c^2=a^2+b^2-2abcosC\)，代值得到\(13=9+b^2-2\times 3\times b\times (-\cfrac{1}{2})\)；

化简得到\(b^2+3b-4=0\)，解得\(b=1\)或\(b=-4\)(舍负)，故\(AC=1\)，选\(A\)。

反思：在具体题目中到底应该选正弦定理还是余弦定理来解三角形，应该具体分析，当然还需要我们搞清楚这两个定理能解决的基本类型，以便于更好的使用。

【2016全国卷Ⅲ】在\(\Delta ABC\)中，已知\(\angle B=\cfrac{\pi}{4}\)，\(BC\)边上的高等于\(\cfrac{1}{3}BC\)，则\(sinA\)=【】

$A、\cfrac{3}{10}$ $B、\cfrac{\sqrt{10}}{10}$ $C、\cfrac{\sqrt{5}}{5}$ $D、\cfrac{3\sqrt{10}}{10}$

分析：做出BC边的高线AD，由于注意到有了两个直角三角形，且\(\angle B=\cfrac{\pi}{4}\)，

则可以引入参数，设\(AD=x\)，则\(BD=x\)，\(AB=\sqrt{2}x\)，

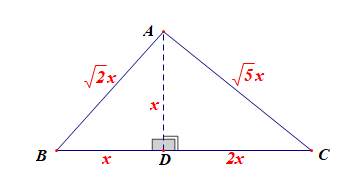
由题目可知\(BC=3x\)，则\(CD=3x-x=2x\) ，\(AC=\sqrt{5}x\)，

到此，在\(\Delta ABC\)中，三边都已经表示出来，且知道一个角，用正弦定理可得

\(\cfrac{\sqrt{5}x}{sin45^{\circ}}=\cfrac{3x}{sin\angle BAC}\)，化简得到\(sin\angle BAC=\cfrac{3\sqrt{10}}{10}\)，故选D

【解后反思】1、大胆引入参数，最后往往就会在运算中消失于无形；2、特别要注意特殊的直角三角形的边角关系，要熟记于心，以便于灵活运用。3、本题当然还可以先用余弦定理求得\(cosA\)，再求得\(sinA\)，但是走了弯路。

【2016全国卷Ⅲ】已知\(\Delta ABC\)的内角为\(A、B、C\)，\(2sinA=\sqrt{3}sinB=3sinC\)，则\(cosB\)的值为多少？

分析：设\(2sinA=\sqrt{3}sinB=3sinC=k\)，

则\(sinA=\cfrac{k}{2}\)，\(sinB=\cfrac{k}{\sqrt{3}}\)，\(sinC=\cfrac{k}{3}\)，

则有\(a：b：c=sinA：sinB：sinC\)，即\(a：b：c=\cfrac{k}{2}：\cfrac{k}{\sqrt{3}}：\cfrac{k}{3}=3：2\sqrt{3}：2\)

由此再设得到\(a=3m\)，\(b=2\sqrt{3}m\)，\(a=2m(m>0)\)(引入非零比例因子的好处)，

由余弦定理可知，\(cosB=\cfrac{a^2+c^2-b^2}{2ac}=\cfrac{9m^2+4m^2-12m^2}{2\cdot 3m\cdot 2m}=\cfrac{1}{12}\)。

反思：1、灵活运用比例的性质，会大大简化运算；2、非零比例因子的引入，也要注意学习运用。

在锐角\(\Delta ABC\)中，角\(A，B，C\)所对的边分别为\(a，b，c\)，若\(sinA=\cfrac{2\sqrt{2}}{3}\)，\(a=3\)，\(S_{\Delta ABC}=2\sqrt{2}\)，则\(b\)的值为【 】

$A、6$ $B、3$ $C、2$ $D、2或3$

分析：由于\(S_{\Delta ABC}=\cfrac{1}{2}bcsinA=2\sqrt{2}\)，则有\(bc=6\)，

又因为\(sinA=\cfrac{2\sqrt{2}}{3}\)，所以\(cosA=\cfrac{1}{3}\)(题目已知锐角三角形)，又\(a=3\)，

由余弦定理得\(a^2=9=b^2+c^2-2bccosA=b^2+c^2-4\)，

即\(b^2+c^2=13\)，结合\(bc=6\)，

可得\(b=2\)或\(b=3\)。故选\(D\).

在\(\Delta ABC\)中， 若\(A=\cfrac{\pi}{4}\)，\(b^2sinC=4\sqrt{2}sinB\)，则\(\Delta ABC\)的面积为___________。

分析：由\(b^2sinC=4\sqrt{2}sinB\)，角化边得到\(b^2c=4\sqrt{2}b\)，

故\(bc=4\sqrt{2}\)，\(S_{\Delta ABC}=\cfrac{1}{2}bcsinA=\cfrac{1}{2}\times 4\sqrt{2} \times \cfrac{\sqrt{2}}{2}=2\)。

在\(\Delta ABC\)中，角\(A、B、C\)的对边分别为\(a、b、c\)，若\(bsinA-\sqrt{3}cosB=0\)，且\(b^2=ac\)，则\(\cfrac{a+c}{b}\)的值为【】

$A、\cfrac{\sqrt{2}}{2}$ $B、\sqrt{2}$ $C、2$ $D、4$

分析：边化角，得到\(sinBsinA-\sqrt{3}sinAcosB=0\)，由于\(sinA\neq 0\)，

得到\(tanB=\sqrt{3}\)，则\(B=\cfrac{\pi}{3}\)，

由余弦定理得到\(b^2=a^2+c^2-2accosB=a^2+c^2-ac\)，

变形一：又\(b^2=ac\)，代入上式，得到\(a^2+c^2-ac=ac\)，解得\(a=c\)，又\(B=\cfrac{\pi}{3}\)，

即三角形是等边三角形，则\(a=b=c\)，故\(\cfrac{a+c}{b}=2\)；故选\(C\)；

变形二：由\(b^2=a^2+c^2-2accosB=a^2+c^2-ac\)得到，\(b^2=(a+c)^2-3ac\)，

又\(b^2=ac\)，代入上式替换\(ac\)，得到\(4b^2=(a+c)^2\)，求得\(\cfrac{a+c}{b}=2\)；故选\(C\)；

在\(\Delta ABC\)中，角\(A、B、C\)的对边分别为\(a、b、c\)，若\(b=1\)，\(a=2c\)，则当\(C\)取最大值时，\(\Delta ABC\)的面积为【】

$A、\cfrac{\sqrt{3}}{3}$ $B、\cfrac{\sqrt{3}}{6}$ $C、\cfrac{2\sqrt{3}}{3}$ $D、\sqrt{3}$

分析：当\(C\)取到最大值时，\(cosC\)取得最小值，故先研究\(cosC\)，

\(cosC=\cfrac{a^2+b^2-c^2}{2ab}=\cfrac{3c^2+1}{4c}\)

\(=\cfrac{1}{4}(3c+\cfrac{1}{c})\ge \cfrac{1}{4}\cdot 2\sqrt{3}=\cfrac{\sqrt{3}}{2}\)，

当且仅当\(3c=\cfrac{1}{c}\)，即\(c=\cfrac{\sqrt{3}}{3}\)时取得等号；

且此时\(sinC=\cfrac{1}{2}\)，故当\(C\)取到最大值时，

\(S_{\Delta ABC}=\cfrac{1}{2}absinC\)

\(=\cfrac{1}{2}\cdot 2c\cdot 1\cdot \cfrac{1}{2}=\cfrac{\sqrt{3}}{6}\)，

故选\(B\)。

【2018·浙江省名校协作体高三联考】在\(\Delta ABC\)中，内角\(A，B，C\)所对的边分别为\(a，b，c\)，已知\(c＝2\)，\(C＝\cfrac{\pi}{3}\)，Ⅰ、当\(2sin2A＋sin(2B＋C)＝sinC\) 时，求\(\Delta ABC\)的面积；

分析：由\(2sin2A+sin(2B＋C)＝sinC\)，

得到\(4sinAcosA+sin[(A+B+C)+B-A]=sinC\)，即\(4sinAcosA+sin[\pi+B-A]=sinC\)，

即\(4sinAcosA-sin(B-A)=sin(B+A)\)，即\(4sinAcosA=sin(B-A)+sin(B+A)\)，

则\(4sinAcosA=2sinBcosA\)，即\(cosA(2sinA-sinB)=0\)，

①当\(cosA=0\)时，\(A=\cfrac{\pi}{2}\)，由\(C＝\cfrac{\pi}{3}\)，得到\(B=\cfrac{\pi}{6}\)；

此时，\(b=\cfrac{2\sqrt{3}}{3}\)，\(S_{\Delta ABC}=\cfrac{1}{2}bcsinA=\cfrac{1}{2}\cdot 2\cdot \cfrac{2\sqrt{3}}{3}=\cfrac{2\sqrt{3}}{3}\)；

②当\(cosA\neq 0\)时，则有\(sinB=2sinA\)，即\(b=2a\)，

由\(\left\{\begin{array}{l}{a^2+b^2-ab=4}\\{b=2a}\end{array}\right.\)，解得\(b=\cfrac{4\sqrt{3}}{3}\)，\(b=\cfrac{2\sqrt{3}}{3}\)，

故\(S_{\Delta ABC}=\cfrac{1}{2}absinC=\cfrac{1}{2}\cdot \cfrac{4\sqrt{3}}{3}\cdot \cfrac{2\sqrt{3}}{3}\cdot\cfrac{1}{2}=\cfrac{2\sqrt{3}}{3}\)；

综上所述，\(S_{\Delta ABC}=\cfrac{2\sqrt{3}}{3}\)；

Ⅱ、求\(\Delta ABC\)周长的最大值。

分析：具体解法见求三角形的周长类的取值范围

【2019届高三理科数学第三轮模拟训练题】在\(\triangle ABC\)中，内角\(A，B，C\)所对的边分别为\(a，b，c\)，设向量\(\vec{n}=(\sqrt{3}a+c，sinB-sinA)\)，\(\vec{m}=(a+b，sinC)\)，若\(\vec{m}//\vec{n}\)，则角\(B\)的大小为【】

$A.\cfrac{\pi}{6}$ $B.\cfrac{\pi}{3}$ $C.\cfrac{5\pi}{6}$ $D.\cfrac{2\pi}{3}$

分析：由\(\vec{m}//\vec{n}\)，得到\(\cfrac{\sqrt{3}a+c}{a+b}=\cfrac{sinB-sinA}{sinC}=\cfrac{b-a}{c}\)，

得到\(c^2+a^2-b^2=-\sqrt{3}ac\)，则\(cosB=-\cfrac{\sqrt{3}}{2}\)，又\(B\in (0，\pi)\)，故\(B=\cfrac{5\pi}{6}\)。

在\(\triangle ABC\)中，\(a=5\)，\(b=4\)，\(cos(A-B)=\cfrac{31}{32}\)，求\(cosC\)的值。

分析：如下图所示，在\(BC\)上取一点\(D\)，使得\(BD=AD=x\)，则\(CD=5-x\)，\(\angle DAB=\angle B\)，则\(\angle CAD=\angle A-\angle B\)，

在\(\triangle ACD\)中，由余弦定理可得，

\(cos\angle CAD=\cfrac{x^2+4^2-(5-x)^2}{2\cdot 4\cdot x}=\cfrac{31}{32}\)，解得\(x=4\)，

故在\(\triangle ABC\)中，由余弦定理可得，\(cosC=\cfrac{1^2+4^2-4^2}{2\times 4\times 1}=\cfrac{1}{8}\)。

【2019届高三理科数学三轮模拟试题】在\(\triangle ABC\)中，内角\(A，B，C\)所对的边分别为\(a，b，c\)，\(AD\)为\(\angle BAC\)的平分线，且满足\(4\overrightarrow{AD}=\overrightarrow{AC}+3\overrightarrow{AB}\)，\(|\overrightarrow{AD}|=\sqrt{3}\)，若\(4c+a=8\)，求\(a\)，\(b\)，\(c\)的值；

分析：由\(4\overrightarrow{AD}=\overrightarrow{AC}+3\overrightarrow{AB}\)，可得\(3\overrightarrow{AD}-3\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{AD}\)，

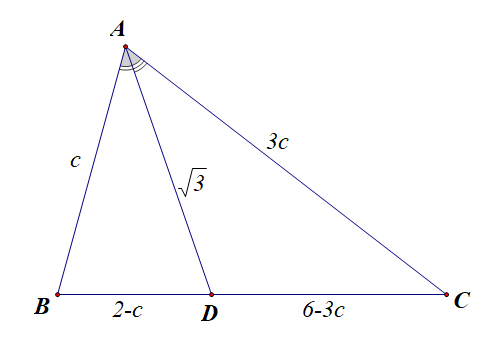
即\(3\overrightarrow{BD}=\overrightarrow{DC}\)，即\(|CD|=3|BD|\)，又\(4c+a=8\)，

则\(a=8-4c=|BC|\)，\(|BD|=\cfrac{1}{4}|BC|=2-c\)，\(|CD|=6-2c\)，

又由于\(AD\)为\(\angle BAC\)的平分线，由角平分线定理可知，

\(\cfrac{BD}{CD}=\cfrac{AB}{AC}=\cfrac{1}{3}\)，故\(|AC|=3C\)，

在\(\triangle ABD\)与\(\triangle ACD\)中，分别对\(\angle BAD\)和\(\angle DAC\)用余弦定理可得，

\(\cfrac{3+c^2-(2-c)^2}{2\times \sqrt{3}c}=\cfrac{3+(3c)^2-(6-3c)^2}{2\times \sqrt{3}\times 3c}\)

解得\(c=\cfrac{5}{4}\)，\(b=\cfrac{15}{4}\)，\(a=3\)。

【2019年高考数学试卷理科新课标Ⅱ第15题】\(\triangle ABC\)的内角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，若\(b=6\)，\(a=2c\)，\(B=\cfrac{\pi}{3}\)，则\(\triangle ABC\)的面积为__________。

分析：利用正余弦定理解三角形。

解析：自行做出相应图形，针对\(b\)边使用余弦定理，得到

\(b^2=a^2+c^2-2accosB\)，即\(36=c^2+4c^2-2\cdot c\cdot 2c\cdot cos\cfrac{\pi}{3}\)

解得，\(c=2\sqrt{3}\)，则\(a=4\sqrt{3}\)，

则\(S_{\triangle ABC}=\cfrac{1}{2}accosB=\cfrac{1}{2}\times 2\sqrt{3}\times 4\sqrt{3}\times \cfrac{\sqrt{3}}{2}=6\sqrt{3}\)。

已知\(\Delta ABC\)中，\(sin(A-\cfrac{\pi}{4})=\cfrac{7\sqrt{2}}{26}\)，若\(\Delta ABC\)的面积为\(24\)，\(c=13\)，求\(a\)的值。

分析：由\(sin(A-\cfrac{\pi}{4})=\cfrac{7\sqrt{2}}{26}\)，估算\(A\)为锐角，打开整理得到\(sinA-cosA=\cfrac{7}{13}\)，结合勾股数\(5，12，13\)可知，

\(sinA=\cfrac{12}{13}，cosA=\cfrac{5}{13}\)，由\(S_{\Delta}=\cfrac{1}{2}bcsinA=\cfrac{1}{2}\times b\times 13\times\cfrac{12}{13}=24\)，

解得\(b=4\)，由余弦定理可得\(a^2=b^2+c^2-2bccosA=16+169-2\times 4\times 13 \times \cfrac{5}{13}=145\)，故\(a=\sqrt{145}\).

【2021届高三理科数学月考三第17题】已知①\(b^2\)\(+\)\(\sqrt{2}ac\)\(=\)\(a^2\)\(+\)\(c^2\)，②\(a\cos B\)\(=\)\(b\sin A\)，③\(\sin B\)\(+\)\(\cos B\)\(=\)\(\sqrt{2}\)，在这三个条件中任选一个，补充在下面的问题中，并解决问题.

已知\(\triangle ABC\)的内角\(A\)，\(B\)，\(C\)的对边为\(a\)，\(b\)，\(c\)，_____________，\(A=\cfrac{\pi}{3}\)，\(b=\sqrt{2}\)，求\(\triangle ABC\)的面积；

分析：由①\(b^2+\sqrt{2}ac=a^2+c^2\)可得，\(\cos B=\cfrac{\sqrt{2}}{2}\)，则\(B=\cfrac{\pi}{4}\)；

由②\(a\cos B=b\sin A\)可得，\(\sin A\cos B=\sin B\sin A\)，即\(\sin B=\cos B\)，则\(B=\cfrac{\pi}{4}\)；

由③\(\sin B+\cos B=\sqrt{2}\)可得，\(\sqrt{2}sin(B+\cfrac{\pi}{4})=\sqrt{2}\)，即\(sin(B+\cfrac{\pi}{4})=1\)，则\(B=\cfrac{\pi}{4}\)；

故不论选择哪一个，通过不同的变形，都会得到条件\(B=\cfrac{\pi}{4}\)，故原问题等价于：

已知\(\triangle ABC\)的内角\(A\)，\(B\)，\(C\)的对边为\(a\)，\(b\)，\(c\)，\(B=\cfrac{\pi}{4}\)，\(A=\cfrac{\pi}{3}\)，\(b=\sqrt{2}\)，求\(\triangle ABC\)的面积；

则由正弦定理\(\cfrac{a}{\sin A}=\cfrac{b}{\sin B}\)，可得\(a=\sqrt{3}\)，

故\(S_{\triangle ABC}=\cfrac{1}{2}ab\sin C=\cfrac{1}{2}ab\sin (A+B)=\cfrac{1}{2}\times\sqrt{2}\times\sqrt{3}\times\sin(\cfrac{\pi}{4}+\cfrac{\pi}{3})\)

\(=\cfrac{3+\sqrt{3}}{4}\)；