三角函数给值求值

前言

三角函数的求值，对许多学生而言，都是个噩梦，我们不妨借助这篇博文梳理思路。

考察角度

角度一：已知角是一个，未知角也是一个角

【教材习题改编】已知\(sin(\alpha-\cfrac{\pi}{3})=\cfrac{15}{17}\)，\(\alpha\in(\cfrac{\pi}{2}，\cfrac{5\pi}{6})\)，则\(sin\alpha\)的值为【】

分析：如果已知的角为一个，如\(\alpha-\cfrac{\pi}{3}\)，未知角也是一个，如\(\alpha\)，此时二者之间的关系往往利用互余、互补、半角、倍角、特殊角的角度建立联系，

比如本题目\(\alpha=(\alpha-\cfrac{\pi}{3})+\cfrac{\pi}{3}\)，

故\(sin\alpha=sin[(\alpha-\cfrac{\pi}{3})+\cfrac{\pi}{3}]=sin(\alpha-\cfrac{\pi}{3})cos\cfrac{\pi}{3}+cos(\alpha-\cfrac{\pi}{3})sin\cfrac{\pi}{3}=\cfrac{15+8\sqrt{3}}{34}\).

• 备注：简单题目只需要用到互余、互补、半角、倍角、特殊角中的某一个角度就可以求解；

【2017枣庄模拟】设\(\alpha\)为锐角，\(cos(\alpha+\cfrac{\pi}{6})=\cfrac{4}{5}\)，求\(sin(2\alpha+\cfrac{\pi}{12})\)的值；

分析：注意到已知角为一个\(\alpha+\cfrac{\pi}{6}\)，未知角也是一个\(2\alpha+\cfrac{\pi}{12}\)，

故二者之间的联系可能是从余、补、半、倍、特的角度建立联系，

故将已知角二倍得到\(2(\alpha+\cfrac{\pi}{6})=2\alpha+\cfrac{\pi}{3}\)，发现还是和未知角不一样，故做差就发现，

\[2\alpha+\cfrac{\pi}{12}=2(\alpha+\cfrac{\pi}{6})-\cfrac{\pi}{4} \]

故\(sin(2\alpha+\cfrac{\pi}{12})=sin[2(\alpha+\cfrac{\pi}{6})-\cfrac{\pi}{4}]\)

\(=sin[2(\alpha+\cfrac{\pi}{6})]cos\cfrac{\pi}{4}-cos[2(\alpha+\cfrac{\pi}{6})]sin\cfrac{\pi}{4}\)

\(=2sin(\alpha+\cfrac{\pi}{6})cos(\alpha+\cfrac{\pi}{6})cos\cfrac{\pi}{4}-[2cos^2(\alpha+\cfrac{\pi}{6})-1]sin\cfrac{\pi}{4}\)

\(=\cdots=\cfrac{17\sqrt{2}}{50}\).

• 备注：复杂一些的题目可能需要用到互余、互补、半角、倍角、特殊角中的某两个以上的角度才可以求解；

【2016·福建师大附中月考】若\(sin(\cfrac{\pi}{3}-\alpha)=\cfrac{1}{4}\)，则\(cos(\cfrac{2\pi}{3}+2\alpha)\)=【】

$A、-\cfrac{7}{8}$ $B、-\cfrac{1}{4}$ $C、\cfrac{1}{4}$ $D、\cfrac{7}{8}$

分析：\(cos(\cfrac{2\pi}{3}+2\alpha)=cos[\pi-(\cfrac{\pi}{3}-2\alpha)]\)

\(=-cos[2(\cfrac{\pi}{3}-\alpha)]=-1+2sin^2(\cfrac{\pi}{3}-\alpha)\)

\(=-1+2\times (\cfrac{1}{4})^2=-\cfrac{7}{8}\)，故选A。

【2017黑龙江哈尔滨六中模拟】已知\(sin(\alpha+\cfrac{\pi}{3})+cos(\alpha-\cfrac{\pi}{2})=-\cfrac{4\sqrt{3}}{5}\)，则\(cos(\alpha+\cfrac{2\pi}{3})\)的值为_____。

分析：先将已知条件变形为\(\sqrt{3}sin(\alpha+\cfrac{\pi}{6})=-\cfrac{4\sqrt{3}}{5}\)，

即\(sin(\alpha+\cfrac{\pi}{6})=-\cfrac{4}{5}\)，求\(cos(\alpha+\cfrac{2\pi}{3})\)；

到此题目的要求明显多了，就是个给值求值题目；

故这样变形，\(cos(\alpha+\cfrac{2\pi}{3})=cos(\alpha+\cfrac{\pi}{6}+\cfrac{\pi}{2})=-sin(\alpha+\cfrac{\pi}{6})=\cfrac{4}{5}\)；

【2020\(\cdot\)河南洋阳一模】设 \(0^{\circ}<\alpha<90^{\circ}\)， 若 \(\sin(75^{\circ}+2\alpha)\)\(=\)\(-\cfrac{3}{5}\)， 则\(\sin(15^{\circ}+\alpha)\)\(\cdot\)\(\sin(75^{\circ}-\alpha)\)=__________

解析：因为 \(0^{\circ}<\alpha<90^{\circ}\)， 所以 \(75^{\circ}<75^{\circ}+2\alpha<255^{\circ}\)，

又因为 \(\sin(75^{\circ}+2\alpha)=-\cfrac{3}{5}<0\)， 所以 \(180^{\circ}<75^{\circ}+2\alpha<255^{\circ}\)，

又由于角 \(75^{\circ}+2\alpha\) 为第三象限角，所以 \(\cos(75^{\circ}+2\alpha)=-\cfrac{4}{5}\)

又由于\(\sin(75^{\circ}-\alpha)=\cos(15^{\circ}+\alpha)\)，[注意：动态角的互余关系]

所以 \(\sin(15^{\circ}+\alpha)\cdot\sin(75^{\circ}-\alpha)=\sin(15^{\circ}+\alpha)\cdot\cos(15^{\circ}+\alpha)\)

\(=\cfrac{1}{2}\sin(30^{\circ}+2\alpha)=\cfrac{1}{2}\sin [(75^{\circ}+2\alpha)-45^{\circ}]\)

\(=\cfrac{1}{2}[\sin(75^{\circ}+2\alpha)\cos45^{\circ}-\cos(75^{\circ}+2\alpha)\cdot\sin 45^{\circ}]\)

\(=\cfrac{1}{2}\times(-\cfrac{3}{5}\times \cfrac{\sqrt{2}}{2}+\cfrac{4}{5}\times\cfrac{\sqrt{2}}{2})=\cfrac{\sqrt{2}}{20}\)

• 角度二：已知角为两个，未知角为一个角，此时常常用两个已知角的线性表示来刻画未知角

【2016聊城模拟】若\(tan\alpha=-\cfrac{1}{2}\)，\(tan(\alpha-\beta)=-\cfrac{2}{5}\)，求\(tan\beta\)的值。

分析：如果已知的角为两个，如\(\alpha\)和\(\alpha-\beta\)；未知角是一个，如\(\beta\)，此时二者之间的关系往往利用两个已知角的和差就能凑出未知角，比如本题目\(\beta=\alpha-(\alpha-\beta)\)

故\(tan\beta=tan[\alpha-(\alpha-\beta)]=\cfrac{tan\alpha-tan(\alpha-\beta)}{1+tan\alpha\cdot tan(\alpha-\beta)}=-\cfrac{1}{12}\)

已知\(sin\alpha+sin\beta=\sqrt{3}(cos\beta-cos\alpha)\)，\(\alpha，\beta\in (0，\cfrac{\pi}{2})\)，则\(sin3\alpha+sin3\beta=\underline{0}\)

分析：由题目\(sin\alpha+sin\beta=\sqrt{3}(cos\beta-cos\alpha)\)，则\(sin\alpha+\sqrt{3}cos\alpha=\sqrt{3}cos\beta-sin\beta\)，

即\(cos(\alpha-\cfrac{\pi}{6})=cos(\beta+\cfrac{\pi}{6})\)，

又\(\alpha-\cfrac{\pi}{6}\in(-\cfrac{\pi}{6}，\cfrac{\pi}{3})\)，\(\beta+\cfrac{\pi}{6}\in(\cfrac{\pi}{6}，\cfrac{2\pi}{3})\)，

则有\(\alpha-\cfrac{\pi}{6}=\beta+\cfrac{\pi}{6}\)，即\(\alpha=\beta+\cfrac{\pi}{3}\)

故\(sin3\alpha+sin3\beta=sin3(\beta+\cfrac{\pi}{3})+sin3\beta\)

\(=sin(3\beta+\pi)+sin3\beta=-sin3\beta+sin3\beta=0\)

已知 \(\alpha\) 为锐角， \(\beta\) 为第二象限角，且 \(\cos(\alpha-\beta)=\cfrac{1}{2}, \sin(\alpha+\beta)=\cfrac{1}{2},\) 则 \(\sin(3\alpha-\beta)\)=【\(\quad\)】

$A.-\cfrac{1}{2}$ $B.\cfrac{1}{2}$ $C.\cfrac{\sqrt{3}}{2}$ $D.-\cfrac{\sqrt{3}}{2}$

法一: 因为 \(\alpha\) 为锐角， \(\beta\) 为第二象限角，

则有\(0<\alpha<\cfrac{\pi}{2}\)，\(2k\pi+\cfrac{\pi}{2}<\beta<2k\pi+\pi\)，\(k\in \Z\)，

故有\(2k\pi-\pi<\alpha-\beta<2k\pi\)，\(2k\pi+\cfrac{\pi}{2}<\alpha+\beta<2k\pi+\cfrac{3\pi}{2}\)，\(k\in \Z\)，

又由于\(\cos (\alpha-\beta)>0\)，\(\sin (\alpha+\beta)>0\)，

所以 \(\alpha-\beta\) 为第四象限角， \(\alpha+\beta\) 为第二象限角，

因此 \(\sin(\alpha-\beta)=-\cfrac{\sqrt{3}}{2}\)，\(\cos(\alpha+\beta)=-\cfrac{\sqrt{3}}{2}\)

所以 \(\sin2\alpha=\sin(\alpha-\beta+\alpha+\beta)=-\cfrac{\sqrt{3}}{2}\times(-\cfrac{\sqrt{3}}{2})+\cfrac{1}{2}\times\cfrac{1}{2}=1\)

因为 \(\alpha\) 为锐角，所以\(2\alpha=\cfrac{\pi}{2}\)，

所以 \(\sin(3\alpha-\beta)=\sin(2\alpha+\alpha-\beta)=\cos(\alpha-\beta)=\cfrac{1}{2}\)，选 \(B\).

法二: 因为 \(\alpha\) 为锐角， \(\beta\) 为第二象限角，

则有\(0<\alpha<\cfrac{\pi}{2}\)，\(2k\pi+\cfrac{\pi}{2}<\beta<2k\pi+\pi\)，\(k\in \Z\)，

故有\(2k\pi-\pi<\alpha-\beta<2k\pi\)，\(2k\pi+\cfrac{\pi}{2}<\alpha+\beta<2k\pi+\cfrac{3\pi}{2}\)，\(k\in \Z\)，

又由于\(\cos (\alpha-\beta)>0\)，\(\sin (\alpha+\beta)>0\)，

所以 \(\alpha-\beta\) 为第四象限角， \(\alpha+\beta\) 为第二象限角，

因此 \(\sin(\alpha-\beta)=-\cfrac{\sqrt{3}}{2}\)，\(\cos(\alpha+\beta)=-\cfrac{\sqrt{3}}{2}\)，

所以 \(\cos2(\alpha-\beta)=2\cos^{2}(\alpha-\beta)-1=2\times(\cfrac{1}{2})^{2}-1=-\cfrac{1}{2}\)，

\(\sin2(\alpha-\beta)=2\sin(\alpha-\beta)\cos(\alpha-\beta)=2\times(-\cfrac{\sqrt{3}}{2})\times\cfrac{1}{2}=-\cfrac{\sqrt{3}}{2}\)，

所以 \(\sin(3\alpha-\beta)=\sin[2(\alpha-\beta)+(\alpha+\beta)]\)

\(=\sin2(\alpha-\beta)\cos(\alpha+\beta)+\cos2(\alpha-\beta)\sin(\alpha+\beta)\)

\(=(-\cfrac{\sqrt{3}}{2})\times(-\cfrac{\sqrt{3}}{2})+(-\cfrac{1}{2})\times\cfrac{1}{2}=\cfrac{1}{2}\)，故选\(B\).

设\(\alpha\)、\(\beta\)都是锐角，且\(cos\alpha=\cfrac{\sqrt{5}}{5}\)，\(sin(\alpha+\beta)=\cfrac{3}{5}\)，则\(cos\beta\)等于【\(\qquad\)】

$A.\cfrac{2\sqrt{5}}{25}$ $B.\cfrac{2\sqrt{5}}{5}$ $C.\cfrac{2\sqrt{5}}{25}或\cfrac{2\sqrt{5}}{5}$ $D.\cfrac{2\sqrt{5}}{25}或\cfrac{\sqrt{5}}{5}$

分析：由已知可得：\(sin\alpha=\cfrac{2\sqrt{5}}{5}\)，\(cos(\alpha+\beta)=\pm\cfrac{4}{5}\)，

若\(cos(\alpha+\beta)=\cfrac{4}{5}>\cfrac{\sqrt{5}}{5}=cos\alpha\)，则有\(\alpha+\beta<\alpha\)，

即\(\beta<0\)，这与\(\beta\)为锐角矛盾舍去，故\(cos(\alpha+\beta)=-\cfrac{4}{5}\)，

所以\(cos\beta=cos[(\alpha+\beta)-\alpha]\)

\(=cos(\alpha+\beta)cos\alpha+sin(\alpha+\beta)sin\alpha\)

\(=\cfrac{2\sqrt{5}}{25}\)，故选\(A\)。

已知\(\alpha\)为第Ⅳ象限角，且\(sin(\alpha+\cfrac{\pi}{4})=\cfrac{3}{5}\)，求\(tan(\alpha-\cfrac{\pi}{4})\)的值；

法1：由题目可知，\(\cfrac{\sqrt{2}}{2}(sin\alpha+cos\alpha)=\cfrac{3}{5}\)，则\(sin\alpha+cos\alpha=\cfrac{3\sqrt{2}}{5}\)，

和\(sin^2\alpha+cos^2\alpha=1\)联立，得到\(2sin^2\alpha-\cfrac{6\sqrt{2}}{5}sin\alpha-\cfrac{7}{25}=0\)，即\((\sqrt{2}sin\alpha+\cfrac{1}{5})(\sqrt{2}sin\alpha-\cfrac{7}{5})=0\)

解得\(sin\alpha=-\cfrac{\sqrt{2}}{10}\)，或\(sin\alpha=\cfrac{7\sqrt{2}}{10}\)(不符，舍去)，

即\(sin\alpha=-\cfrac{\sqrt{2}}{10}\)，\(cos\alpha=\cfrac{7\sqrt{2}}{10}\)，从而\(tan\alpha=-\cfrac{1}{7}\)

代入\(tan(\alpha-\cfrac{\pi}{4})=\cfrac{tan\alpha-1}{1+tan\alpha}=-\cfrac{4}{3}\)；

法2：由\(sin\alpha+cos\alpha=\cfrac{3\sqrt{2}}{5}\)，得到\(2sin\alpha cos\alpha=-\cfrac{7}{25}\)，

则有\((sin\alpha-cos\alpha)^2=\cfrac{32}{25}\)，由于\(\alpha\)为第Ⅳ象限角，

得到\(sin\alpha-cos\alpha=-\cfrac{4\sqrt{2}}{5}\)，又\(sin\alpha+cos\alpha=\cfrac{3\sqrt{2}}{5}\)，

即\(sin\alpha=-\cfrac{\sqrt{2}}{10}\)，\(cos\alpha=\cfrac{7\sqrt{2}}{10}\)，从而\(tan\alpha=-\cfrac{1}{7}\)

代入\(tan(\alpha-\cfrac{\pi}{4})=\cfrac{tan\alpha-1}{1+tan\alpha}=-\cfrac{4}{3}\)；

法3：由\(2sin\alpha cos\alpha=-\cfrac{7}{25}\)，得到\(\cfrac{2sin\alpha cos\alpha}{sin^2\alpha+cos^2\alpha}=-\cfrac{7}{25}\)，

则\(\cfrac{2tan\alpha}{tan^2\alpha+1}=-\cfrac{7}{25}\)，解得\(tan\alpha=-7\)或\(tan\alpha=-\cfrac{1}{7}\)，

又由于又\(sin\alpha+cos\alpha=\cfrac{3\sqrt{2}}{5}\)，则\(|cos\alpha|>|sin\alpha|\)，即\(|tan\alpha|<1\)，

故保留\(tan\alpha=-\cfrac{1}{7}\)，代入\(tan(\alpha-\cfrac{\pi}{4})=\cfrac{tan\alpha-1}{1+tan\alpha}=-\cfrac{4}{3}\)；

已知\(\sin(\theta-\cfrac{\pi}{4})=\cfrac{2\sqrt{2}}{3}\)，则\(\sin2\theta\)的值为【】

$A.\cfrac{7}{9}$ $B.-\cfrac{7}{9}$ $C.\cfrac{2}{9}$ $D.-\cfrac{2}{9}$

[法1]：从数的角度分析，借助三角函数的变换求解；将已知的角看成两个角\(\theta\)和\(\cfrac{\pi}{4}\)的差，

由于\(\sin(\theta-\cfrac{\pi}{4})=\cfrac{2\sqrt{2}}{3}\)，即\(\sin\theta\cdot \cfrac{\sqrt{2}}{2}-\cos\theta\cdot \cfrac{\sqrt{2}}{2}=\cfrac{2\sqrt{2}}{3}\),

整理得到，\(\sin\theta-\cos\theta=\cfrac{4}{3}\)，两边平方得到\(1-\sin2\theta=\cfrac{16}{9}\)

则\(\sin2\theta=-\cfrac{7}{9}\)，故选\(B\);

[法2]：从数的角度分析，借助三角函数的变换求解；将已知的角\(\theta-\cfrac{\pi}{4}\)看成一个整体角，

\(\sin2\theta=\cos(\cfrac{\pi}{2}-2\theta)=\cos2(\cfrac{\pi}{4}-\theta)=\cos2(\theta-\cfrac{\pi}{4})\)

\(=1-2\sin^2(\theta-\cfrac{\pi}{4})=1-2\cdot (\cfrac{2\sqrt{2}}{3})^2=-\cfrac{7}{9}\)，故选\(B\);

[法3]：从形的角度分析，借助三角函数线求解；

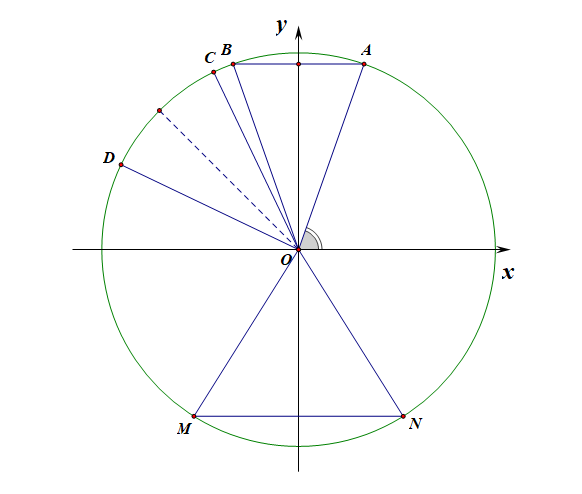
做平面直角坐标系和单位圆，由\(\sin(\theta-\cfrac{\pi}{4})=\cfrac{2\sqrt{2}}{3}\)可知，

则角\(\theta-\cfrac{\pi}{4}\)的终边位于射线\(OA\)或\(OB\)上，其关于\(y\)轴对称，

将其顺时针旋转\(\cfrac{\pi}{4}\)，得到角\(\theta\)的终边位于射线\(OC\)或\(OD\)上，其关于\(y=-x\)轴对称，

将角\(\theta\)乘以\(2\)倍，则得到角\(2\theta\)的终边位于射线\(OM\)或\(ON\)上，其关于\(y\)轴对称，

结合图像，如果做其正弦线，可知首先排除选项\(A\)，\(C\)，比较选项\(B\)，\(D\)，可知应该排除\(D\)，而选\(B\)；

可转化型

【2021届高三文科数学第三轮模拟训练题】已知 \(\alpha\)，\(\beta\in (0,\cfrac{\pi}{2})\)，且 \(\cos\alpha=\cfrac{2\sqrt{5}}{5}\)， \(\cos(\alpha+\beta)=\cfrac{5}{13}\)，则 \(\cos(\alpha-\beta)\)=【\(\quad\)】

$A.\cfrac{21}{65}$ $B.\cfrac{63}{65}$ $C.-\cfrac{33}{65}$ $D.\cfrac{33}{65}$

分析：当由两个已知角 \(\alpha\) 和 \(\alpha+\beta\) 的代数和不能表示未知角时，我们应该考虑能不能得到另外的两个已知角，再来表示未知角，很明显就渗透有转化划归思想在里面。

解析：由题目可知， \(\cos2\alpha=2\cos^2\alpha-1=\cfrac{3}{5}\)，

由于 \(\alpha\)，\(\beta\in (0,\cfrac{\pi}{2})\)，故 \(\sin2\alpha=\cfrac{4}{5}\)，\(\sin(\alpha+\beta)=\cfrac{12}{13}\)，

则 \(\cos(\alpha-\beta)=\cos[2\alpha-(\alpha+\beta)]\)

\(=\cos2\alpha\cdot\cos(\alpha+\beta)+\sin2\alpha\cdot\sin(\alpha+\beta)=\cfrac{63}{65}\)

故选 \(B\).

新题补充

【2019届高三理科数学第三轮模拟训练题】设\(5sin\alpha=2+4cos^2\alpha\)，则\(cos2\alpha\)=________。

分析：由已知条件，解方程得到\(sin\alpha=-2\)(舍去)，\(sin\alpha=\cfrac{3}{4}\)，则\(cos2\alpha=1-2sin^2\alpha=-\cfrac{1}{8}\)。

【2019届高三理科数学第三轮模拟训练题】已知\(\alpha\)为第\(Ⅳ\)象限角，且\(sin(\alpha+\cfrac{\pi}{3})=\cfrac{3}{5}\)，则\(sin(\alpha+\cfrac{\pi}{12})\)=__________.

分析：由\(\alpha\)为第Ⅳ象限角，且\(sin(\alpha+\cfrac{\pi}{3})=\cfrac{3}{5}\)，则\(cos(\alpha+\cfrac{\pi}{3})=\cfrac{4}{5}\)，

则\(sin(\alpha+\cfrac{\pi}{12})=sin[(\alpha+\cfrac{\pi}{3})-\cfrac{\pi}{4}]=\cfrac{3}{5}\times \cfrac{\sqrt{2}}{2}-\cfrac{4}{5}\times \cfrac{\sqrt{2}}{2}=-\cfrac{\sqrt{2}}{10}\)。

【2019届高三理科数学第三轮模拟训练题】已知\(cos(\alpha+\cfrac{\pi}{4})=-\cfrac{5\sqrt{2}}{8}\)，则\(sin2\alpha\)=【】

$A.-\cfrac{5}{8}$ $B.-\cfrac{9}{16}$ $C.\cfrac{9}{16}$ $D.\cfrac{5}{8}$

分析：\(sin2\alpha=-cos(\cfrac{\pi}{2}+2\alpha)=-[2cos^2(\alpha+\cfrac{\pi}{4})^2-1]=-\cfrac{9}{16}\)，故选\(B\).

【2020届高三文科数学训练题】已知\(tan(\alpha+\beta)=2\)，\(tan\beta=3\)，则\(sin2\alpha\)=【】

$A.\cfrac{7}{25}$ $B.\cfrac{14}{25}$ $C.-\cfrac{7}{25}$ $D.-\cfrac{14}{25}$

法1：先求得\(tan\alpha=-\cfrac{1}{7}\)，则\(\cfrac{sin\alpha}{cos\alpha}=\cfrac{-1}{7}=\cfrac{-k}{7k}\)，\((k\neq 0)\)，

则\(sin\alpha=-k\)，\(cos\alpha=7k\)，则由\(k^2+49k^2=1\)得到\(k^2=\cfrac{1}{50}\)，

故\(sin2\alpha=2sin\alpha\cdot cos\alpha=2\times (-k)\times 7k=-14\times k^2=-14\times \cfrac{1}{50}=-\cfrac{7}{25}\)，故选\(C\)。

法2：先求得\(tan\alpha=-\cfrac{1}{7}\)，由二次齐次式可得

\(sin2\alpha=\cfrac{2sina\cdot cos\alpha}{sin^2\alpha+cos^2\alpha}=\cfrac{2tan\alpha}{tan^2\alpha+1}=-\cfrac{7}{25}\)，故选\(C\)。

【2020届高三文科数学训练题】已知\(\alpha\)为第二象限角，\(\sin(\alpha+\cfrac{\pi}{4})=\cfrac{\sqrt{2}}{10}\)，则\(\tan\cfrac{\alpha}{2}\)的值为【】

$A.-\cfrac{1}{2}$ $B.\cfrac{1}{3}$ $C.2$ $D.-3$

法1：由\(\sin(\alpha+\cfrac{\pi}{4})=\cfrac{\sqrt{2}}{2}(\sin\alpha+\cos\alpha)=\cfrac{\sqrt{2}}{10}\)，可以得到\(\sin\alpha+\cos\alpha=\cfrac{1}{5}\)，

又\(\alpha\)为第二象限角，结合勾股数\(3,4,5\)，可知\(\sin\alpha=\cfrac{4}{5}\)，\(\cos\alpha=-\cfrac{3}{5}\)，

\(\tan\cfrac{\alpha}{2}=\cfrac{\sin\cfrac{\alpha}{2}}{\cos\cfrac{\alpha}{2}}\)

\(=\cfrac{\sin\cfrac{\alpha}{2}\cdot 2\cdot\cos\cfrac{\alpha}{2}}{\cos\cfrac{\alpha}{2}\cdot 2\cdot\cos\cfrac{\alpha}{2}}=\cfrac{\sin\alpha}{1+\cos\alpha}\)

\(=\cfrac{\frac{4}{5}}{1-\frac{3}{5}}=2\)， 故选\(C\).

法2：由\(\sin(\alpha+\cfrac{\pi}{4})=\cfrac{\sqrt{2}}{2}(\sin\alpha+\cos\alpha)=\cfrac{\sqrt{2}}{10}\)，可以得到\(\sin\alpha+\cos\alpha=\cfrac{1}{5}\)，

则\(\sin\alpha+\cos\alpha=\cfrac{\sin\alpha+\cos\alpha}{\sin^2\cfrac{\alpha}{2}+\cos^2\cfrac{\alpha}{2}}\)

\(=\cfrac{2\cdot\sin\cfrac{\alpha}{2}\cdot \cos\cfrac{\alpha}{2}+\cos^2\cfrac{\alpha}{2}-\sin^2\cfrac{\alpha}{2}}{\sin^2\cfrac{\alpha}{2}+\cos^2\cfrac{\alpha}{2}}\)

\(=\cfrac{2\tan\cfrac{\alpha}{2}-\tan^2\cfrac{\alpha}{2}+1}{\tan^2\cfrac{\alpha}{2}+1}=\cfrac{1}{5}\)

解得，\(\tan\cfrac{\alpha}{2}=2\)或\(\tan\cfrac{\alpha}{2}=-\cfrac{1}{3}\)，

由于\(\alpha\)为第二象限角，由八卦图法可知，\(\tan\cfrac{\alpha}{2}>0\)，故\(\tan\cfrac{\alpha}{2}=2\)，故选\(C\).

【2021届高三文科数学资料训练题】已知\(\tan\cfrac{\alpha}{2}=3\)，则\(\cos\alpha\)=【\(\quad\)】

$A.\cfrac{4}{5}$ $B.-\cfrac{4}{5}$ $C.\cfrac{4}{15}$ $D.-\cfrac{3}{5}$

分析：\(\cos\alpha=\cos^2\cfrac{\alpha}{2}-\sin^2\cfrac{\alpha}{2}=\cfrac{\cos^2\cfrac{\alpha}{2}-\sin^2\cfrac{\alpha}{2}}{\cos^2\cfrac{\alpha}{2}+\sin^2\cfrac{\alpha}{2}}\)

\(=\cfrac{1-\tan^2\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}=\cfrac{1-9}{1+9}=-\cfrac{4}{5}\)；故选\(B\).