三角不等式的解法

前言

廓清认知：由于三角不等式属于超越不等式，故已经不能和解 $x^2+3x+2>0$ 这样的代数不等式的解法同日而语，此时必须借助图像来解决；能借助的图像有三角函数的图像，还可以借助三角函数线来解决，以下用例题加以说明。

必备技能

函数图像的解读能力
作三角函数$y=sinx$和$y=cosx$的图像、作正弦线、余弦线的能力
用不等式表达单位圆中区域的能力
用韦恩图求交集的能力
转化划归能力

模型应用

解三角不等式： $2sinx>1$.

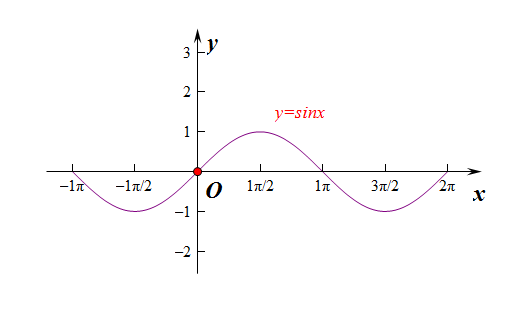
法1：三角函数图像法，将不等式变形为$sinx>\cfrac{1}{2}$，在同一个坐标系中做出函数$y=sinx$和$y=\cfrac{1}{2}$，

由于函数$y=sinx$有周期性，故需要不需要画出其完整的图像，只需要做出一个周期上的图像就可以了，

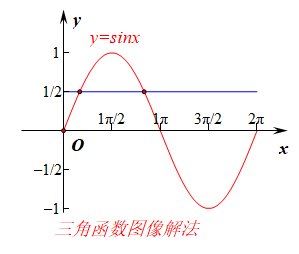
如右图所示，我们选取的周期是$[0，2\pi]$，从图上可以看出，

当$sinx>\cfrac{1}{2}$时，在一个周期内的不等式的解是$\cfrac{\pi}{6}< x <\cfrac{5\pi}{6}$，

而题目中$x\in R$，故我们还需要做出拓展，那么怎么拓展呢？

函数$y=\cfrac{1}{2}$，自然是向左右两端无限延伸的，

函数$y=sinx$也是向左右两端按照周期$T=2\pi$的整数倍无限延伸的，

故满足题意的不等式的解集绝不仅仅是上述解出的解集，

应该还有，就是把上述的解集也向左右两端按照周期的整数倍延伸，

即$k \cdot 2\pi+\cfrac{\pi}{6}< x < k \cdot 2\pi+\cfrac{5\pi}{6}(k\in Z)$，

故所求的不等式的所有解集应该是$\{x\mid 2k\pi+\cfrac{\pi}{6}< x <2k\pi+\cfrac{5\pi}{6}，k\in Z\}$；

或者$(2k\pi+\cfrac{\pi}{6}，2k\pi+\cfrac{5\pi}{6})(k\in Z)$ $\hspace{4em}$错误写法：^[1]

法1的反思提升：

1、周期函数的周期一定要选$[0，2\pi]$吗？

那倒不一定，原则上只要区间的长度为$2\pi$都可以，比如本题还可以选周期为$[-\pi，\pi]$，这样我们可以看到在一个周期内的不等式的解集是连续的，便于我们的表达刻画。

2、如果解$sinx<\cfrac{1}{2}$，周期怎么选？

此时如果还选$[0，2\pi]$，那就不好，由上图我们可以看出，

此时一个周期内的解集有$[0，\cfrac{\pi}{6})$，还有$(\cfrac{5\pi}{6}，2\pi]$，两个解集就没有连续在一起，后续拓展表达很不方便；

那么我们怎么解决这一问题呢？只要选周期为$[\cfrac{\pi}{2}，\cfrac{5\pi}{2}]$就可以，

此时一个周期内的解集就可以表达为$\cfrac{5\pi}{6}< x<\cfrac{13\pi}{6}$，

再拓展得到$R$上的解集为$2k\pi+\cfrac{5\pi}{6} < x<2(k+1)\pi+\cfrac{\pi}{6}(k\in Z)$，

3、如何解不等式$sin(2x+\cfrac{\pi}{4})>\cfrac{1}{2}$？

此时，将整体$2x+\cfrac{\pi}{4}$看成上述解法中的$x$(整体思想)，

先得到$sinx>\cfrac{1}{2}$的解集为$2k\pi+\cfrac{\pi}{6}< x <2k\pi+\cfrac{5\pi}{6}(k\in Z)$；

然后回归，得到$2k\pi+\cfrac{\pi}{6}< 2x+\cfrac{\pi}{4} <2k\pi+\cfrac{5\pi}{6}(k\in Z)$；

解上述的双连不等式就得到不等式$sin(2x+\cfrac{\pi}{4})>\cfrac{1}{2}$的解集。

请自行解决。

4、如何解不等式：$\cfrac{1}{2}\cdot sinx+\cfrac{\sqrt{3}}{2}cosx>\cfrac{1}{2}$.

先将其转化划归为$sin(x+\cfrac{\pi}{3})>\cfrac{1}{2}$，然后仿照上例解决即可。

5、如何解不等式$2cosx\geqslant 1$；

其一可以借助函数$y=cosx$的图像求解即可。其二，可以借助单位圆和三角函数线法；此时需要注意，解集的区间表示有难点。

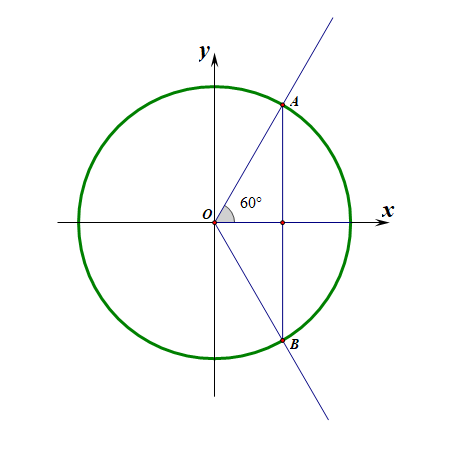
如图所示，满足题意的角的终边应该落在劣弧$AB$所对的扇形区域内，由于此时$x$轴的正半轴包含在其中，故表示时射线$OB$应该用$2k\pi-\cfrac{\pi}{3}$刻画，射线$OA$应该用$2k\pi+\cfrac{\pi}{3}$刻画，

即解集应该为$[2k\pi-\cfrac{\pi}{3},2k\pi+\cfrac{\pi}{3}]$$(k\in Z)$，

【易错】①好多学生在此容易错误的认为，射线$OB$应该用$2k\pi+\cfrac{5\pi}{3}$刻画，此时是错误的，原因是若解集为$[2k\pi+\cfrac{5\pi}{3},2k\pi+\cfrac{\pi}{3}]$$(k\in Z)$，明显区间特点为左大右小，故错误；

②还有学生会纠结，为什么表示角的终边在$y$轴负半轴时，可以用$2k\pi+\cfrac{3\pi}{2}$$(k\in Z)$，也可以用$2k\pi-\cfrac{\pi}{2}$$(k\in Z)$，为什么上题中这样使用就是错误的？原因是上题表示的结果是一个区域，边界线射线$OB$不是孤立存在的，与别人有大小关系，故不能随心所欲的表示；

③如何选取区域，做一条角的终边落在某个区域内，然后验证即可。角的终边定区域[线性规划中，特殊点定区域]

[例1的法2]：三角函数线法，做出如右图所示的单位圆，在$y$轴的正半轴找到$\cfrac{1}{2}$，

过此点做$x$轴的平行线与单位圆交于点$P$和点$Q$，

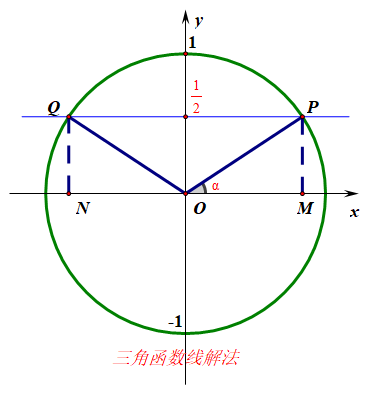
则$sinx=\cfrac{1}{2}$时的正弦线是$MP$和$NQ$，那么$sinx>\cfrac{1}{2}$时的角的终边应该落在劣弧$OPQ$内部，

故在一个周期内的不等式的解是$\cfrac{\pi}{6}< x <\cfrac{5\pi}{6}$，

拓展后得到$R$上的解集为$\{x\mid k \cdot 2\pi+\cfrac{\pi}{6}< x < k \cdot 2\pi+\cfrac{5\pi}{6}(k\in Z)\}$；

当然，如果是解不等式$sinx<\cfrac{1}{2}$ ，则角的终边应该落在优弧$OPQ$内，

在一个周期内的不等式的解是$-\cfrac{7\pi}{6}< x <\cfrac{\pi}{6}$，

拓展后得到$R$上的解集为$\{x \mid k \cdot 2\pi-\cfrac{7\pi}{6}< x < k \cdot 2\pi+\cfrac{\pi}{6}(k\in Z)\}$；

化为模型

解不等式：$2cos(2x+\cfrac{\pi}{3})<1$

提示：先想这样的不等式怎么解？$2cosx<1$；

然后再思考$2cos(2x+\cfrac{\pi}{3})<1$怎么解即可。

【可转化为例2】解不等式：$\cfrac{1}{2}\cdot sinx+\cfrac{\sqrt{3}}{2}cosx<\cfrac{1}{2}$.

看看例1中的提示就够了。

综合应用

函数 $y=\sqrt{\sin x-\cos x}$的定义域为___________.

法1：三角函数图像法，

要使函数有意义，必须使 $\sin x-\cos x \geqslant 0$，

利用图像，在同一平面直角坐标系中画出$y=\sin x$和$y=\cos x$的图像[注释：这样的手工作图，在高三的三角函数学习中，非常多见，提醒掌握]，

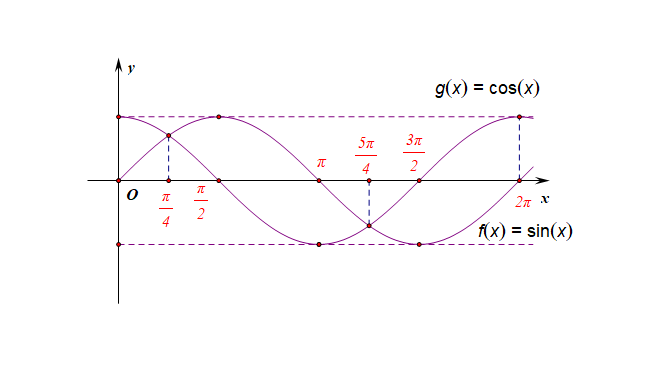
由图像可知，在$[0, 2\pi]$ 内，当$\cfrac{\pi}{4} \leqslant x \leqslant \cfrac{5\pi}{4}$ 时， $\sin x-\cos x \geqslant 0$ ，

又正弦、余弦函数的周期是 $2\pi$，所以原函数的定义域为

$\{x \mid 2k\pi+\cfrac{\pi}{4}\leqslant x \leqslant 2k\pi+\cfrac{5\pi}{4}, k \in Z\}$

法2：单位圆+三角函数线法，

借助单位圆和三角函数线，可以看出，

当$\theta$的终边落在直线$y=x$上时，$sin\theta=cos\theta$；

当$\theta$的终边落在直线$y=x$右下方时，$sin\theta<cos\theta$；

当$\theta$的终边落在直线$y=x$左上方时，$sin\theta>cos\theta$；

由图像可知，在$[0, 2\pi]$ 内，当$\cfrac{\pi}{4} \leqslant x \leqslant \cfrac{5 \pi}{4}$ 时， $\sin x-\cos x \geqslant 0$ ，

又正弦、余弦函数的周期是 $2\pi$，所以原函数的定义域为

$\{x \mid 2k\pi+\cfrac{\pi}{4}\leqslant x \leqslant 2k\pi+\cfrac{5\pi}{4}, k \in Z\}$

法3：模型法，对于高三的学生，基本都知道[下述的模型，最好理解并记忆]，

若$\sin x\geqslant 0$时，解得$2k\pi\leqslant x\leqslant 2k\pi+\pi(k\in Z)$，

由于$\sin x-\cos x\geqslant 0$，即$\sqrt{2}\sin(x-\cfrac{\pi}{4})\geqslant 0$，

即$\sin(x-\cfrac{\pi}{4})\geqslant 0$，比照上述的模型，

可知$2k\pi\leqslant x-\cfrac{\pi}{4}\leqslant 2k\pi+\pi(k\in Z)$，解得，

$2k\pi+\cfrac{\pi}{4}\leqslant x \leqslant 2k\pi+\cfrac{5\pi}{4}，k\in Z$

所以原函数的定义域为$\{x \mid 2k\pi+\cfrac{\pi}{4}\leqslant x \leqslant 2k\pi+\cfrac{5\pi}{4}, k \in Z\}$

求函数$y=\lg sinx+\sqrt{\cos2x+\frac{1}{2}}$的定义域。

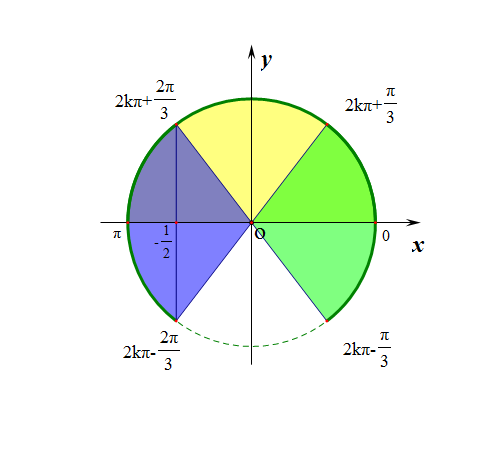
【解析】三角不等式常用两种解法，利用三角函数线或者三角函数图像，详解如下：

【1、单位圆+三角函数线】

如图所示，由正弦线可知，$sinx>0$得到：$x\in(2k\pi，2k\pi+\pi)(k\in Z)$

由余弦线可知，$cos2x\ge-\cfrac{1}{2}$

得到：$2x\in[2k\pi-\cfrac{2\pi}{3}，2k\pi+\cfrac{2\pi}{3}](k\in Z)$，

所以$x\in[k\pi-\cfrac{\pi}{3}，k\pi+\cfrac{\pi}{3}]\\=[2k\pi-\cfrac{\pi}{3}，2k\pi+\cfrac{\pi}{3}]\bigcup[2k\pi+\cfrac{2\pi}{3}，2k\pi+\cfrac{4\pi}{3}](k\in Z)$，

求其交集得到$x\in(2k\pi，2k\pi+\cfrac{\pi}{3}]\bigcup[2k\pi+\cfrac{2\pi}{3}，2k\pi+\pi)(k\in Z)$

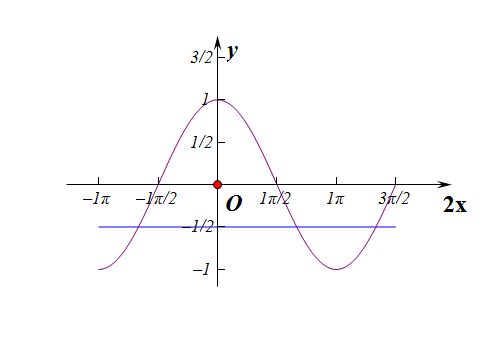
【2、三角函数法】转化为解三角函数不等式组$\begin{cases} sinx> 0 \\ cos2x+\frac{1}{2}\ge 0\end{cases}$，

解不等式$sinx>0$

得到：$x\in(2k\pi，2k\pi+\pi)(k\in Z)$

解不等式$cos2x\ge-\cfrac{1}{2}$

得到：$2x\in[2k\pi-\cfrac{2\pi}{3}，2k\pi+\cfrac{2\pi}{3}](k\in Z)$，

所以$x\in[k\pi-\cfrac{\pi}{3}，k\pi+\cfrac{\pi}{3}](k\in Z)$，

求其交集得到$x\in(2k\pi，2k\pi+\cfrac{\pi}{3}]\bigcup[2k\pi+\cfrac{2\pi}{3}，2k\pi+\pi)(k\in Z)$

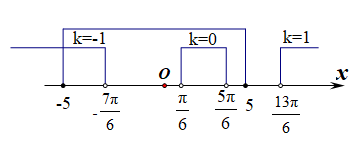
【求三角不等式和其他不等式的交集】求函数$f(x)=\sqrt{5-|x|}+log_a(sinx-\cfrac{1}{2})$的定义域。

分析：由题目可知，$|x|\leq 5①$，且$sinx>\cfrac{1}{2}②$

解①得到$-5\leq x\leq 5$；解②得到$2k\pi+\cfrac{\pi}{6}<x<2k\pi+\cfrac{5\pi}{6}(k\in Z)$，

二者求交集，如右图所示，

得到定义域为$[-5，-\cfrac{7\pi}{6})\cup (\cfrac{\pi}{6}，\cfrac{5\pi}{6})$。

正切不等式

求直线的倾斜角取值范围，本质是解正切型三角不等式。直线的倾斜角的范围$\theta\in [0，\pi)$；

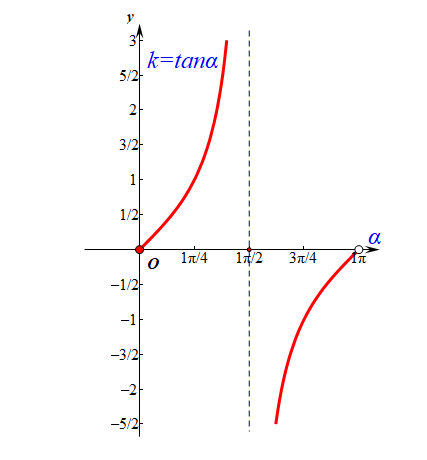
直线$2xcos\alpha-y-3=0(\alpha\in [\cfrac{\pi}{6}，\cfrac{\pi}{3}])$的倾斜角的变化范围是【】

$A.[\cfrac{\pi}{6}，\cfrac{\pi}{3}]$ $B.[\cfrac{\pi}{4}，\cfrac{\pi}{3}]$ $C.[\cfrac{\pi}{4}，\cfrac{\pi}{2})$ $D.[\cfrac{\pi}{4}，\cfrac{2\pi}{3}]$

分析：设直线的倾斜角为$\theta$，则$k=tan\theta=2cos\alpha$，由于$\alpha\in [\cfrac{\pi}{6}，\cfrac{\pi}{3}]$，则$2cos\alpha\in [1，\sqrt{3}]$，

即$k=tan\theta\in [1，\sqrt{3}]$，故$\theta\in [\cfrac{\pi}{4}，\cfrac{\pi}{3}]$，故选$B$.

直线$xsin\alpha-y+1=0$的倾斜角的变化范围是【】

$A.(0，\cfrac{\pi}{2})$ $B.(0，\pi)$ $C.[-\cfrac{\pi}{4}，\cfrac{\pi}{4}]$ $D.[0，\cfrac{\pi}{4}]\cup[\cfrac{3\pi}{4}，\pi)$

分析：设直线的倾斜角为$\theta$，则$k=tan\theta=sin\alpha\in [-1，1]$，又由于$\theta\in [0，\pi)$，

则$\theta\in [0，\cfrac{\pi}{4}]\cup[\cfrac{3\pi}{4}，\pi)$，故选$D$.

【2014黄冈模拟】直线$l$经过$A(2，1)$、$B(1，m^2)(m\in R)$两点，那么直线$l$的倾斜角的取值范围为【】

$A.[0，\pi)$ $B.[0，\cfrac{\pi}{4}]\cup[\cfrac{3\pi}{4}，\pi)$ $C.[0，\cfrac{\pi}{4}]$ $D.[0，\cfrac{\pi}{4}]\cup(\cfrac{\pi}{2}，\pi)$

分析：由点$A(2，1)$、$B(1，m^2)$得到，$k=tan\theta=\cfrac{m^2-1}{1-2}=1-m^2\leqslant 1$，故$\theta\in [0，\cfrac{\pi}{4}]\cup(\cfrac{\pi}{2}，\pi)$，故选$D$.

静+雅