三角形的各种线的向量刻画 | 难点
用向量刻画三角形中的各种常用线段对应的向量
前言
三角形中的各种常用的线段，若换用向量形式的符号语言来刻画，则大多学生可能会极度恐惧，因此有必要将三角形中常用的各种线段的向量表示形式好好作以总结储备。
常用结论
1、与非零向量 \(\vec{a}\) 共线的单位向量 \(\vec{a_0}\) 为两个，\(\vec{a_0}=\pm\cfrac{\vec{a}}{|\vec{a}|}\)；\(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\) 刻画的是和向量 \(\overrightarrow{AB}\) 同方向的单位向量 ， \(-\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\) 刻画的是和向量 \(\overrightarrow{AB}\) 反方向的单位向量 .
2、在 \(\triangle ABC\) 中，令 \(\overrightarrow{AB}=\vec{a}\)，\(\overrightarrow{AC}=\vec{b}\)，以 \(\{\overrightarrow{AB},\overrightarrow{AC}\}\) 为基底，则用基底向量的线性组合就可以表示三角形中的各种线对应的向量。如图所示，\(AD\)，\(AE\)，\(AF\) 分别是三角形的底边 \(BC\) 上的中线、角平分线，高线；\(L\) 为平面内一点，
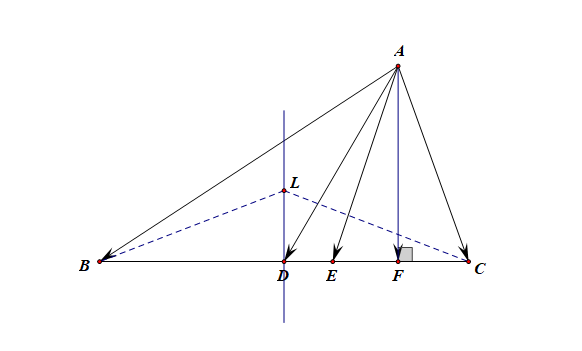
三角形的中线向量：\(\overrightarrow{AD}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\cfrac{1}{2}(\vec{a}+\vec{b})\)；
三角形的中垂线向量：\(|\overrightarrow{LB}|=|\overrightarrow{LC}|\)，则 \(LD\) 为中垂线；
三角形的高线向量：\(\overrightarrow{AF}\cdot\overrightarrow{CB}=0\)，\(\overrightarrow{AF}\cdot(\overrightarrow{AB}-\overrightarrow{AC})=0\)，\(\overrightarrow{AF}\cdot(\vec{a}-\vec{b})=0\)，\(\overrightarrow{AF}\cdot\vec{a}-\overrightarrow{AF}\cdot\vec{b}=0\)，
三角形的角平分线向量：\(\overrightarrow{AE}\)\(=\)\(\lambda(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})\)\(=\)\(\lambda(\cfrac{\vec{a}}{|\vec{a}|}\)\(+\)\(\cfrac{\vec{b}}{|\vec{b}|})\) 或 \(\overrightarrow{AE}\)\(\cdot\)\((\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(-\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})=0\) [1]
三角形的顶角平分线和底边高线重合的刻画：\(\bigg(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\bigg)\)\(\cdot\)\(\overrightarrow{BC}\)\(=\)\(0\)，
三角形的顶角平分线和底边中线重合的刻画：\(\bigg(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\bigg)\) \(//(\overrightarrow{AB}+\overrightarrow{AC})\)
典例剖析
法1： 本题目中，表达式 \(\bigg(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\bigg)\) 刻画的是 \(\angle A\) 的角平分线向量，
由题目可知，\(\bigg(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\bigg)\)\(\cdot\)\(\overrightarrow{BC}\)\(=\)\(0\)，则说明 \(\angle A\) 的平分线和 \(BC\) 边垂直，则三角形 \(\triangle ABC\) 为等腰三角形，[顶角平分线和底边高线合一的三角形是等腰三角形]
又 \(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(\cdot\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\)\(=\)\(\cfrac{1}{2}\)，说明和向量 \(\overrightarrow{AB}\)、 \(\overrightarrow{AC}\)同方向的单位向量的内积为\(\cfrac{1}{2}\)，所以 \(\cos A=\cfrac{1}{2}\)，则 \(\angle A=60^{\circ}\) .
故三角形 \(\triangle ABC\) 为等边三角形， 选 \(D\) .
法2： 由 \(\bigg(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\bigg)\)\(\cdot\)\(\overrightarrow{BC}\)\(=\)\(0\)，将向量 \(\overrightarrow{BC}\) 分配进去得到，\(\cfrac{\overrightarrow{AB}\cdot\overrightarrow{BC}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}\cdot\overrightarrow{BC}}{|\overrightarrow{AC}|}\)\(=\)\(0\)，
即 \(\cfrac{|\overrightarrow{AB}||\overrightarrow{BC}|\cos(\pi-B)}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{|\overrightarrow{AC}||\overrightarrow{BC}|\cos C}{|\overrightarrow{AC}|}\)\(=\)\(0\)，
即 \(\cos(\pi-B)\)\(+\)\(\cos C\)\(=\)\(0\)，即 \(-\cos B+\cos C=0\)，即 \(B=C\) ，
又 \(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(\cdot\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\)\(=\)\(\cfrac{1}{2}\)，说明和向量 \(\overrightarrow{AB}\)、 \(\overrightarrow{AC}\)同方向的单位向量的内积为\(\cfrac{1}{2}\)，所以 \(\cos A=\cfrac{1}{2}\)，则 \(\angle A=60^{\circ}\) .
故三角形 \(\triangle ABC\) 为等边三角形， 选 \(D\) .
解析：由 \((\overrightarrow{BA}+\overrightarrow{BC})\cdot \overrightarrow{AC}=0\) 得到， \(\cfrac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})\cdot \overrightarrow{AC}=0\) ，而 \(\cfrac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})\) 对应的形是三角形的边 \(AC\) 上的中线向量，且其同时还为三角形的高线，这样中线和高线重合的三角形为等腰三角形，即 \(BA=BC\) ；
又由\(\bigg|\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(+\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\bigg|\)\(=\)\(\sqrt{3}\)可知，\(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\) 刻画的是和向量 \(\overrightarrow{AB}\) 同方向的单位向量，这样我们令 \(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}=\vec{e_1}\)，\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}=\vec{e_2}\)，则由 \(|\vec{e_1}+\vec{e_2}|=\sqrt{3}\)，平方可得，\(\vec{e_1}\cdot\vec{e_2}=\cfrac{1}{2}\)，故可以求得 \(A=60^{\circ}\)，这样有一个角为 \(60^{\circ}\) 的等腰三角形是等边三角形，故选 \(B\) .
中线长公式
\(m_{a}=\cfrac{1}{2}\sqrt{2(b^2+c^2)-a^2}\)；\(m_{b}=\cfrac{1}{2}\sqrt{2(c^2+a^2)-b^2}\)；\(m_{c}=\cfrac{1}{2}\sqrt{2(a^2+b^2)-c^2}\)；
证明：以 \(m_{a}=\cfrac{1}{2}\sqrt{2(b^2+c^2)-a^2}\) 的证明为例；如下图所示，\(AD\) 为 \(BC\) 边的中线，\(|AD|=m_a\)
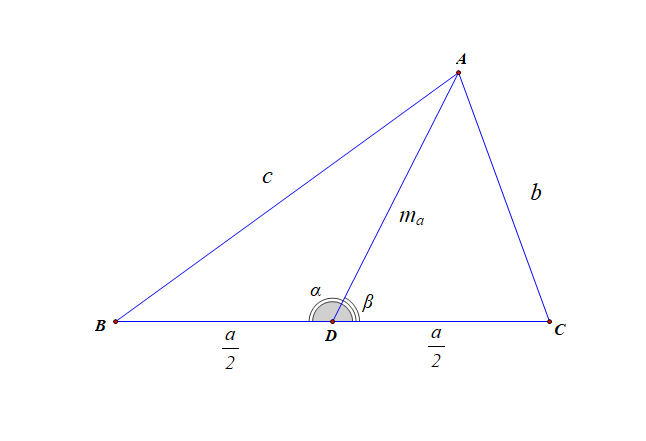
在 \(\triangle ABD\) 中，由余弦定理可知，\(c^2=m_a^2+(\cfrac{a}{2})^2-2\times m_a\times\cfrac{a}{2}\times\cos\alpha\) ①，
在 \(\triangle ACD\) 中，由余弦定理可知，\(b^2=m_a^2+(\cfrac{a}{2})^2-2\times m_a\times\cfrac{a}{2}\times\cos\beta\) ②，
由于 \(\cos\alpha+\cos\beta=0\)，①+② 得到，
\(b^2+c^2=2\times m_a^2+\cfrac{a^2}{2}\)，整理即得到，\(m_{a}=\cfrac{1}{2}\sqrt{2(b^2+c^2)-a^2}\) ，证毕 。
其他中线公式，可以仿此证明。
证明: 由向量的三角形法则可知， \(\overrightarrow{AD}\)\(=\)\(\cfrac{1}{2}(\overrightarrow{AB}\)\(+\)\(\overrightarrow{AC})\)
同时平方，得到 \(AD^2\)\(=\)\(\cfrac{1}{4}\)\(\left(AB^2 + AC^2 + 2AB \cdot AC\cdot\cos A\right)\)
然后将 \(\cos A=\cfrac{AB^2 + AC^2 - BC^2}{2AB \cdot AC}\) 代入上式，得到
\(AD^2\)\(=\)\(\cfrac{1}{4}\)\(\left(AB^2 + AC^2 + 2AB \cdot AC \cdot \cfrac{AB^2 + AC^2 - BC^2}{2AB \cdot AC}\right)\)
化简，得 \(AD^2\)\(=\)\(\cfrac{1}{4}\)\(\left(2AB^2 + 2AC^2 - BC^2\right)\)
证明：延长中线 \(AD\) 到 \(E\) ，使得 \(AD=DE\)，连接 \(EB\)、\(EC\)，则得到 \(\large▱\)\(ABEC\)，
我们知道，在平行四边形中，四边的平方和等于对角线的平方和 [2]，由此得到，
\(2AB^2+2AC^2=BC^2+AE^2=BC^2+4AD^2\)，整理得到， \(AD^2\)\(=\)\(\cfrac{1}{4}\)\((2AB^2\)\(+\)\(2AC^2\)\(-\)\(BC^2)\) .
角平分线长公式
由于 \(S_{\triangle ABC}\)\(=\)\(S_{\triangle ABD}\)\(+\)\(S_{\triangle CBD}\)，
结合三角形正弦型的面积公式 \(S_{\triangle ABC}=\cfrac{1}{2}ab\sin C\)，两边同时乘 2，得到
\(ac\sin B\)\(=\)\(c\cdot\)\(BD\sin\cfrac{B}{2}\)\(+\)\(a\cdot\)\(BD\sin\cfrac{B}{2}\)，
左边用二倍角公式展开，得到 \(2ac\)\(\sin\cfrac{B}{2}\)\(\cos\cfrac{B}{2}\)\(=\)\((a+c)\)\(BD\)\(\sin\cfrac{B}{2}\)
两边约去 \(\sin\cfrac{B}{2}\)，得到 \(BD\)\(=\)\(\cfrac{2ac\cos\frac{B}{2}}{a+c}\) .
仿上式引申：若 \(\angle A\) 和 \(\angle C\) 的平分线分别为 \(AE\) 和 \(CF\)，则 \(AE\)\(=\)\(\cfrac{2bc\cos\frac{A}{2}}{b+c}\)，\(CF\)\(=\)\(\cfrac{2ab\cos\frac{C}{2}}{a+b}\) .
相关延伸
从数的角度解释如下：\(\overrightarrow{AE}\)\(\cdot\)\((\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(-\)\(\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})=0\)，即 \(\cfrac{\overrightarrow{AE}\cdot\overrightarrow{AB}}{|\overrightarrow{AB}|}\)\(-\)\(\cfrac{\overrightarrow{AE}\cdot\overrightarrow{AC}}{|\overrightarrow{AC}|}\)\(=\)\(0\)，
即 \(\cfrac{|\overrightarrow{AE}||\overrightarrow{AB}|\cos\angle BAE}{|\overrightarrow{AB}|}\)\(-\)\(\cfrac{|\overrightarrow{AE}||\overrightarrow{AC}|\cos\angle CAE}{|\overrightarrow{AC}|}\)\(=\)\(0\)，
即 \(\cos\angle BAE=\cos\angle CAE\)，则 \(\angle BAE=\angle CAE\)，故 \(AE\) 为 \(\angle A\) 的平分线。 ↩︎【初中几何二级结论】在平行四边形中，四边的平方和等于对角线的平方和。即在 \(\large▱\)\(ABCD\) 中，\(AB^2\)\(+\)\(BC^2\)\(+\)\(CD^2\)\(+\)\(DA^2\)\(=\)\(AC^2\)\(+\)\(BD^2\) .
证明：在 \(Rt\triangle BDE\) 中，\(BD^2\)\(=\)\(DE^2\)\(+\)\(BE^2\)\(=\)\(DE^2\)\(+\)\((AB-AE)^2\)\(=\)\(DE^2\)\(+\)\(AB^2\)\(-2AB\)\(\cdot\)\(AE\)\(+\)\(AE^2\)\(=\)\(AD^2\)\(+\)\(AB^2\)\(-2AB\)\(\cdot\)\(AE\)，
同理同法可得，在 \(Rt\triangle ACF\) 中，\(AC^2\)\(=\)\(AD^2\)\(+\)\(AB^2\)\(+2AB\)\(\cdot\)\(AE\)\(=\)\(BC^2\)\(+\)\(DC^2\)\(+2AB\)\(\cdot\)\(AE\) ，
则 \(BD^2\)\(+\)\(AC^2\)\(=\)\(AB^2\)\(+\)\(BC^2\)\(+\)\(CD^2\)\(+\)\(DA^2\)，即 \(AB^2\)\(+\)\(BC^2\)\(+\)\(CD^2\)\(+\)\(DA^2\)\(=\)\(AC^2\)\(+\)\(BD^2\) ，得证 . ↩︎
浙公网安备 33010602011771号
