射影定理
总结初中和高中阶段，我们常接触和使用的射影定理的两种形式。
前言
在初中和高中阶段，我们接触和使用的射影定理有以下两种形式。
射影定理1
直角三角形射影定理，又叫欧几里德(Euclid)定理，其内容：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
符号语言：如图，\(Rt\triangle ABC\)中，\(\angle BAC=90°\)，\(AD\)是斜边\(BC\)上的高，则有射影定理如下：
证明：这主要是由相似三角形来推出的，
例如，证明\(AD^2=BD\cdot DC\)，
在\(\triangle BAD\)与\(\triangle ACD\)中，\(∠B=∠DAC\)，\(∠BDA=∠ADC=90°\)，
故\(\triangle BAD\sim\triangle ACD\)，所以 \(\cfrac{AD}{BD}＝\cfrac{CD}{AD}\)，
所以得到，\(AD^2=BD\cdot DC\). 其余仿此证明；
注：由上述射影定理还可以证明勾股定理。
比如由公式➋+➌得到，
\(AB^2+AC^2=BD\cdot BC+CD\cdot BC=(BD+CD)BC=BC^2\)，
即\(AB^2+AC^2=BC^2\)，这就是勾股定理的结论。
射影定理2
任意三角形射影定理注释：以“\(a\)\(＝\)\(b\cdot\cos C\)\(＋\)\(c\cdot\cos B\)”为例，\(b\)、\(c\)在\(a\)上的射影分别为\(b\cdot\cos C\)、\(c\cdot\cos B\)，故名射影定理。，又称“第一余弦定理”，其内容为：三角形的任意一边的长等于其他两边在这条边上的射影之和。
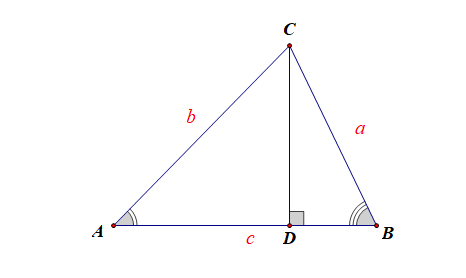
符号语言：设\(\triangle ABC\)的三边是\(a\)、\(b\)、\(c\)，它们所对的角分别是\(A\)、\(B\)、\(C\)，则有：
\(➊a＝b\cdot\cos C\)\(+\)\(c\cdot\cos B\)
\(➋b＝c\cdot\cos A\)\(+\)\(a\cdot\cos C\)
\(➌c＝a\cdot\cos B\)\(+\)\(b\cdot\cos A\)
[证法1]：设点\(C\)在直线\(AB\)上的射影为点\(D\)，
则\(AC\)、\(BC\)在直线\(AB\)上的射影分别为\(AD\)、\(BD\)，
且\(AD=b\cdot\cos A\)，\(BD=a\cdot\cos B\)，
故\(c=AD+BD=b\cdot\cos a+a\cdot\cos B\). 同理可证其余。
[证法2]：由正弦定理，可得：\(b=\cfrac{a\sin B}{\sin A}\)，\(c=\cfrac{a\sin C}{\sin A}\)
即\(c=\cfrac{a\sin(A+B)}{\sin A}=\cfrac{a(\sin A\cos B+\cos A\sin B)}{\sin A}\)
\(=a\cos B+(\cfrac{a\sin B}{\sin A})\cos A=a\cdot\cos B+b\cdot\cos A\). 同理可证其余。
[证法3]：以向量三角形为案例，
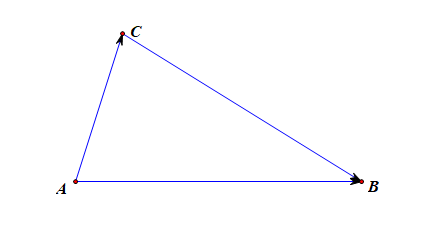
给\(\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}\)，两边同乘以向量\(\overrightarrow{CB}\)，
得到\(\overrightarrow{CB}\cdot\overrightarrow{CB}=(\overrightarrow{AB}-\overrightarrow{AC})\cdot\overrightarrow{CB}\)，
即\(\overrightarrow{CB}^2=\overrightarrow{AB}\cdot\overrightarrow{CB}-\overrightarrow{AC}\cdot\overrightarrow{CB}\)
即\(\overrightarrow{CB}^2=|\overrightarrow{AB}|\cdot|\overrightarrow{CB}|\cdot\cos<\overrightarrow{AB},\overrightarrow{CB}>-|\overrightarrow{AC}|\cdot|\overrightarrow{CB}|\cdot\cos<\overrightarrow{AC},\overrightarrow{CB}>\)
即\(\overrightarrow{CB}^2=|\overrightarrow{AB}|\cdot|\overrightarrow{CB}|\cdot\cos B-|\overrightarrow{AC}|\cdot|\overrightarrow{CB}|\cdot\cos(\pi-C)\)
即\(a^2=c\cdot a\cdot\cos B+b\cdot a\cdot\cos C\)，两边约去\(a\)，
得到\(a=c\cdot\cos B+b\cdot\cos C\)，即得到射影定理，也称第一余弦定理。
使用场景
引例，如解三角形题目中出现这样的条件： \(\cfrac{\sin^2A+\sin^2B-\sin^2C}{c}=\cfrac{\sin A\sin B}{a\cos B+b\cos A}\)，
分析：则我们由射影定理2，将\(a\cdot\cos B+b\cdot\cos A=c\)，代入上式，
即\(\cfrac{\sin^2A+\sin^2B-\sin^2C}{c}=\cfrac{\sin A\sin B}{c}\)，
则得到 \(a^2+b^2-c^2=ab\) ，即已知条件等于告诉我们： \(a^2+b^2-c^2=ab\) ，那么接下来的思路自然就通畅无阻了.
典例剖析
解析: 在 \(\triangle ABC\) 中, \(c=a \cos B+b \cos A\)，[射影定理]
联立 \(\left\{\begin{array}{l}c=a\cos B+b\cos A \\ a\cos B-b\cos A=\cfrac{c}{2}\end{array}\right.，\) 解得\(\cos A=\cfrac{c}{4b}\)，\(\cos B=\cfrac{3c}{4a}\)，
所以 \(\cfrac{a\cos A+b\cos B}{a\cos B}=\cfrac{a\cdot\cfrac{c}{4b}+b\cdot\cfrac{3c}{4a}}{a\cdot\cfrac{3c}{4a}}\)
\(=\cfrac{1}{3}(\cfrac{a}{b}+\cfrac{3 b}{a})\geq\cfrac{1}{3}\times 2\sqrt{\cfrac{a}{b}\cdot\cfrac{3b}{a}}\)
\(=\cfrac{2\sqrt{3}}{3}\)
当且仅当 \(\cfrac{a}{b}=\cfrac{3 b}{a}\) 时，等号成立.
故\(\cfrac{a\cos A+b\cos B}{a\cos B}\) 的最小值为\(=\cfrac{2\sqrt{3}}{3}\)；
【解答】解: 如图, 设球 \(O\) 的半径为 \(R\)， 由题意， \(\cfrac{4}{3} \pi R^{3}=\cfrac{32 \pi}{3}\)，
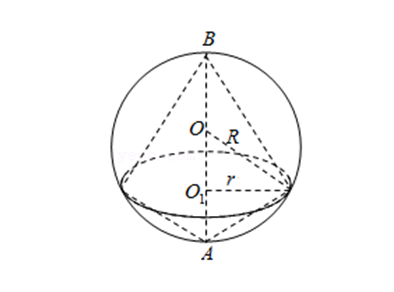
可得 \(R=2\)， 则球 \(O\) 的直径为 \(4\)， 两个圆锥的高之比为 \(1:3\)， \(AO_{1}=1\)， \(B O_{1}=3\)，
由直角三角形中的射影定理可得: \(r^{2}=1\times 3\)， 即 \(r=\sqrt{3}\).
所以这两个圆锥的体积之和为 \(V=\cfrac{1}{3} \pi \times(\sqrt{3})^{2} \times(1+3)=4 \pi\)， 故选: \(B\).
解析：由射影定理可知， \(a\cdot\cos B+b\cdot\cos A=c\)，即已知条件变形为 \(\cfrac{a^2+b^2-c^2}{c}=\cfrac{ab}{c}\)，则 \(a^2+b^2-c^2=ab\)，
从而可知，\(\cos C=\cfrac{1}{2}\)，又 \(c\in (0,\pi)\)，故 \(C=\cfrac{\pi}{3}\) .
