dottle 讲课记录 day 1（dp专项）

上午：DP 奇技淫巧 (斜率优化，决策单调性，wqs 二分）

前置芝士

凸性：

关于凸性，称一个欧式空间的几何体是凸的，当且仅当对于任意几何体内的两点，它们的中点都在几何体内。

称一元函数 𝑓(𝑥) 是下凸的，若几何体 {(𝑥,𝑦)∣𝑓(𝑥)≤𝑦} 是凸的。
可以验证，这等价于：

1. 函数的导数是单调不降的；
2. \(𝑓(𝑥_1 )+𝑓(𝑥_2 )≥2 𝑓((𝑥_1+𝑥_2)/2)\)；
3. 𝑓 的边际效应递增。

1 和 2 是显然的，关于边际效应，你可以这样理解：

边际效应

第一口可乐永远是最好喝的 —— 边际效应递减。

跑 2 次 5km 比跑 1 次 10km 简单很多 —— 边际效应递增。

边际效应对应着决策单调性。

一维的边际效应对应着凸性，而二维的边际效应对应着四边形不等式。

我们这样来刻画二维的边际效应递增：
对于任意区间 \([𝑎,𝑐] 和 [𝑏,𝑐]\)，其中 \(𝑎≤𝑏≤𝑐\)：

\[𝑓(𝑎,𝑐+1)−𝑓(𝑎,𝑐)≥𝑓(𝑏,𝑐+1)−𝑓(𝑏,𝑐) \]

即我们给长区间加一个东西，比给短区间加一个东西代价更大。

此条件等价于对于所有 \(𝑎≤𝑏≤𝑐≤𝑑\)：

\[𝑓(𝑎,𝑑)−𝑓(𝑎,𝑐)≥𝑓(𝑏,𝑑)−𝑓(𝑏,𝑐) \]

此式移项后：

\[𝑓(𝑎,𝑑)+𝑓(𝑏,𝑐)≥𝑓(𝑎,𝑐)+𝑓(𝑏,𝑑) \]

即为我们熟知的四边形不等式。

四边形不等式

可以推出决策单调性，完全单调性，代价关于段数是凸的（凸性）

决策单调性

四边形不等式可以推出决策单调性。（以下为个人见解）

还是注意到给长区间加一个东西，比给短区间加一个东西代价更大这一四边形不等式本质，我们来证明当前决策点不可能在上一个选择的点左边这一决策单调性本质。

举个例子，我们定义当前点到上当前决策点为右边，上一个决策点到当前决策点为左边，\(x\) 为当前决策点。

（如果认为很抽象的话，举个例子，当前问题为划分区间，求每段区间代价之和最小，代价需要经过一系列计算，但是符合四边形不等式，列如代价计算为 \((\sum_{i=l}^r a_i)^3 + K\) ,\(a_i\) 为正整数，显然长区间加一个东西比给短区间加一个东西代价更大，满足四边形不等式)

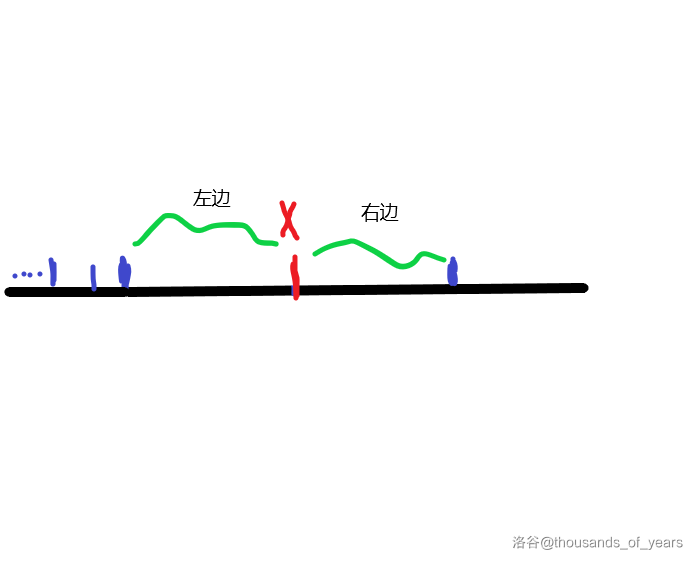
你只考虑你现在要划分的一个区间。因为 \(x-1\) 归左边管，是因为使右边收纳 \(x-1\) 的代价大于左边收纳 \(x-1\) 的代价，当前点持续向右增长，该区间越来越长，右边收纳 \(x-1\) 的代价越来越大，所以以后的决策点不可能向左移动。

反而右边收纳 \(x\) 的代价大于左边收纳 \(x\) 的代价，决策点右移，整个 \(x\) 之前的自动调整为最优划分代价（\(dp_x\)）。

相较于 \(1D/1D\)（任意划分）和 \(2D/1D\)（划分 \(k\) 段）, 前者由于是当层转移，就最多将枚举的起始点往后挪一点，减少一点常数，而后者是通过 \(dp_{k-1}\) 该层转移，可以通过分治方法，将时间复杂度优化为 \(O(n k \log n )\)，具体看 PPT。（个人见解结束）

若 \(𝑤(𝑖,𝑗)\) 只可如用增量法求（像莫队那样），此算法仍然可以做到 \(𝑂(𝑛 \log 𝑛)\)。

完全单调性

对于任意 \(𝑖<𝑗\)，在一个前缀中从 \(𝑖\) 转移更好，在一个后缀中从 \(𝑗\) 转移更好。

这个条件叫完全单调性，它严格强于决策单调性。
满足四边形不等式的代价函数的转移满足完全单调性。

常见方法为二分队列（二分栈），详见 PPT，例题：P1912 \[NOI2009\] 诗人小G

凸完全单调性（wqs 二分）

代价函数符合四边形不等式的划分问题，代价关于段数是凸的。

wqs 二分用于解决这样形式的问题：

1. 选恰好 \(𝑘\) 个元素的最小代价。
2. 将序列划分为恰好 \(𝑘\) 段的最小代价。
   其他的去写分治吧！

核心想法：如果选一个东西有额外的代价，那么我选的就会少一些；如果有额外的奖励，那么我选的就会多一些。

我们在外层二分选一个东西奖惩的 \(k\) 值，跑一遍 1D/1D（跑 dp 中每划分一下 / 每选择一个数加入一次奖惩的 \(k\) 值）。我们设 \(k\) 为选一个东西有额外的代价（为负则为奖励），如果最后段数小于 \(k\)，\(k\) 变小（鼓励多选），如果大于 \(k\)，\(k\) 变大（鼓励少选）。

上方决策单调性的例子在这使用二分队列 + wqs 二分即可达到 \(O(n {log n}^2)\)，比分治更优。

注意二分的边界不能设为恰好选中了所需个元素，因为可能会出现三点共线的情况：\(𝑓^′ (𝑥)=𝑓^′ (𝑥+1)\)，而我们希望选 \(𝑥+1\) 个数。此时参数代入多少都可能不会恰好选 \(𝑥+1\)。因此二分边界是斜率唯一确定，此时 \(𝑔(𝑥+1)\) 一定等于 \(𝑔(𝑥)\)，从而算出 \(𝑓(𝑥+1)\)。

至于为什么不能用于凹函数，是因为加入这个额外代价是相当于相切这个函数，或者说这个函数大体形状并不会变（相当于旋转？），中间凹进去的点无论如何调 \(k\)，都将永远无法成为最值。（要看图想一下 w 形状的图）

斜率优化

这个还会，算法竞赛上讲的写好，就不写了。

下午： 设计方法与奇形怪状的 DP

dp 优化之优化状态

我们无法一次性设计出最好的 dp，抑或是朴素的转移可以利用一些方法进行优化。

对 dp 的优化归根究底要么是优化状态，要么是优化转移。

优化又可以分为两类，一类是利用其他算法加速状态与转移，另一类是剪去无用的状态转移。后者很容易被忽略。

其他算法的加速过于平常，今天让我们先来看看如何剪去无用的状态与转移。

状态设计技巧

我们可以将所有有可能产生影响的变量全部列下来，然后分析哪些变量可以去掉。

在最优化问题中，一个常用的方法是：先设计一个取值为 0/1 的状态，然后利用单调性去掉一维。（例题详见 PPT）

算了，剩下的 PPT 讲的太好了，直接去看 PPT 吧！

各类技巧串讲

以后来补

好的继续，给你一道字符串题，长度为 n 的字符串删去 m 个字符，出现不同字符串个数。题

通过 PPT 的第一页，可以发现判定代码循环外只有一个变量，其判定也只受该变量影响，似乎称为后效性。

\(dp_{i,j}\) 表示当前子序列长为 \(𝑖\)，匹配到了 \(𝑗\) 这一个字符。（不是子序列，应该 i 指当前到哪一位）

在字符串计数类问题中，这是解决的一般方法。

1. 解决判定问题；
2. 把判定问题所需的变量都记录在数组之中。

当我们判定 / 统计字符串的时候，对于已经考虑完了的前 \(𝑖\) 个字符，它们对后面会产生影响的东西全都记在状态里了。

如果我们给出的判定算法是一个 dp，得到的就是 dp 套 dp 了。

好了，剩下的也是题了。