数理逻辑笔记整理
布尔代数
析取:∨,逻辑或
合取:∧,逻辑与,通常省略或使用’·‘(点乘)代替

可以列出的最小元素0,最大元素1和任何元素a及其补a‘都是唯一确定的。

OBDD(有序二元决策树)
将逻辑语言使用二叉决策图的形式表示
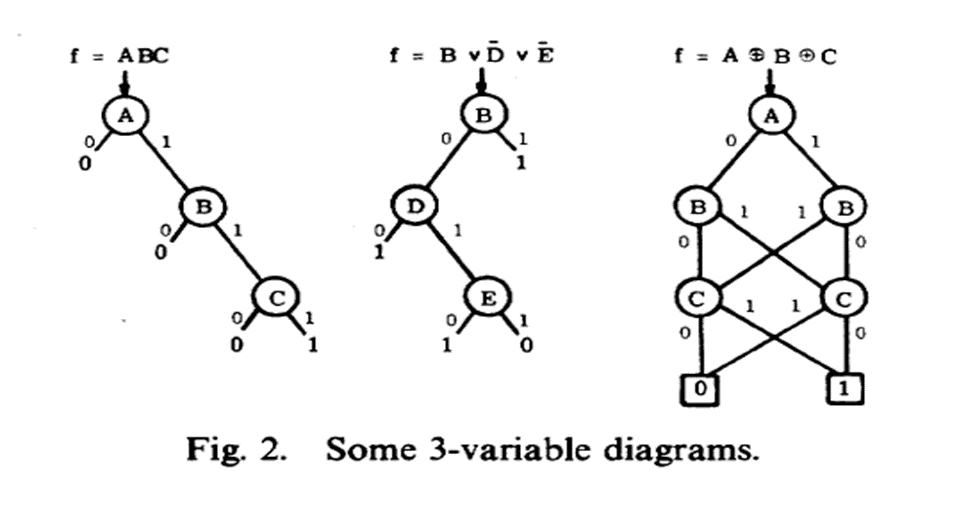
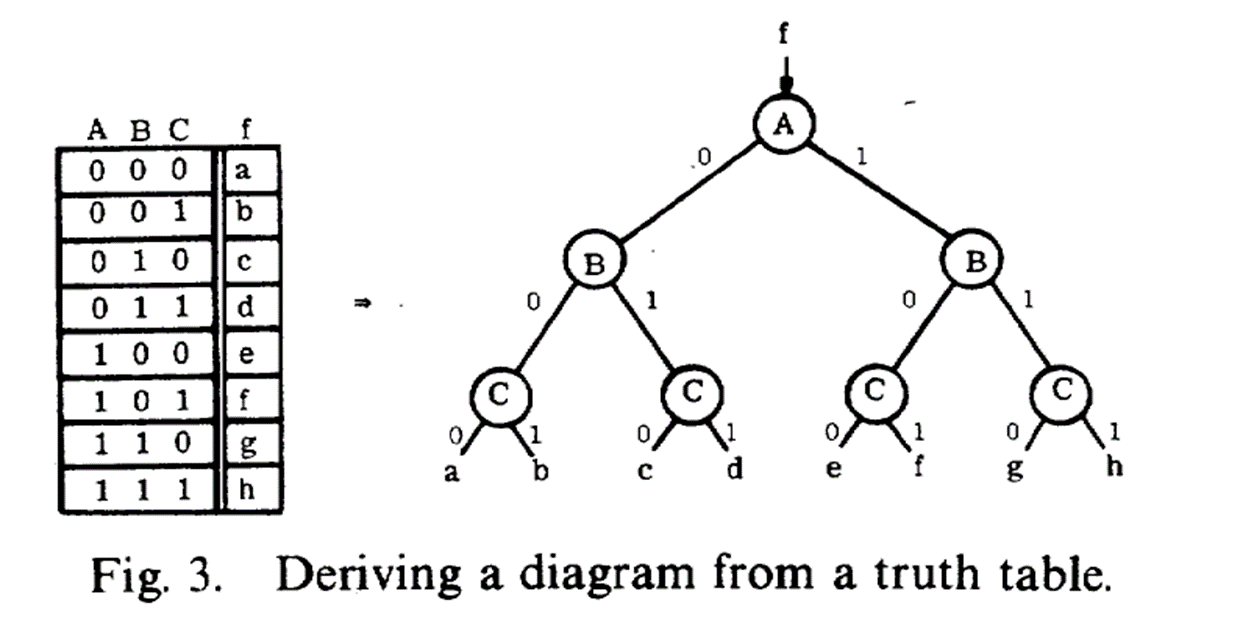
真值表与BDD
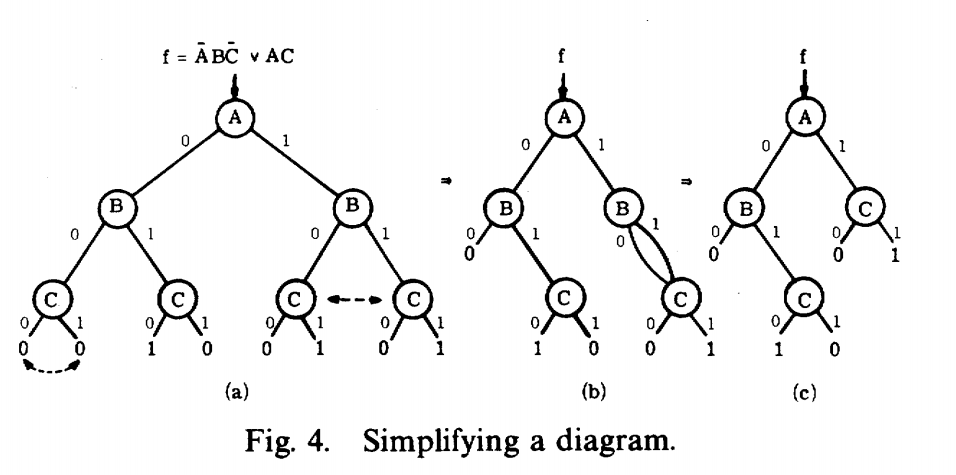
化简:去除冗余部分
香农展开·决策图算法步骤
对于布尔函数的展开:![]()
- 固定一个变量,画出此变量的节点以及0,1分支
- 观察是否有冗余分支存在,存在则合并;否则再选取另一个变量,转至步骤1
- 直至分支节点处变为0或1,结束
总结:逐层确定变量取值,对应改变布尔表达式。
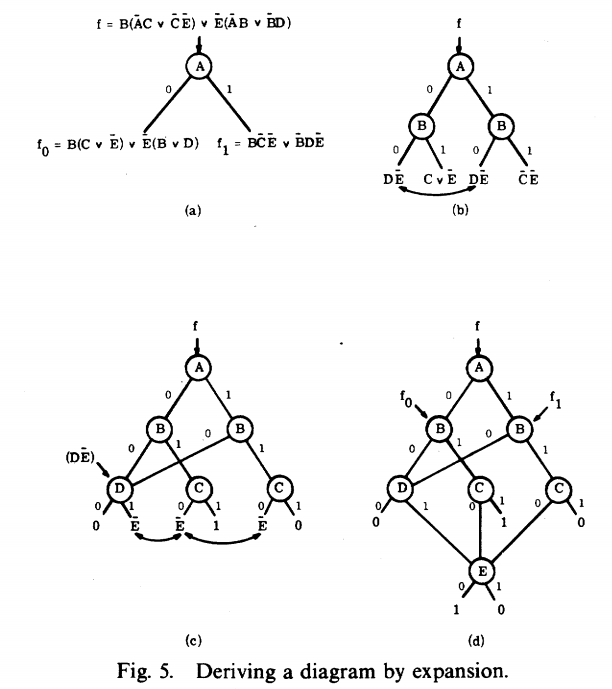
BDD再计算机存储中,每个节点对应一个三元组:<变量名,指针1,指针2>
其中,指针1,2分别指向当前变量取值为0和1时的节点。
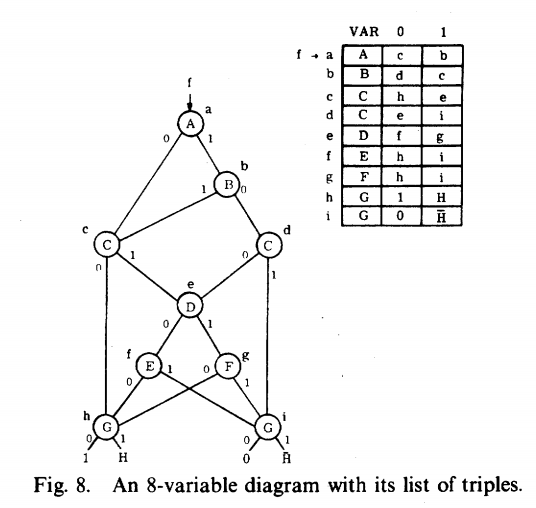
计算BDD输出·算法步骤
- 在图中标识所有被赋值(取决于布尔表达式)的路径,这些路径称为active path
- 沿着active path取至终点。
注:
- 一个节点的输出路径有且仅有一条是active path
- 从一个节点到0或1终点,有且仅有一条由active path组成的路径
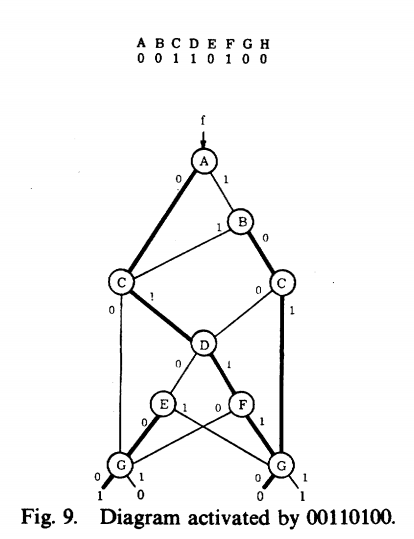
计算“和的积”与“积的和”的个数
“和的积”的个数:主合取范式中,合取式的个数,即:使输出结果为0的路径数目。
“积的和”的个数:主析取范式中,析取式的个数,即:使输出结果为1的路径数目。
用分支的权值计算:
步骤:
- 最上层结点的两个分支权均赋值为1。
- 其余的结点的两个分支权均赋值为它所有入度权值的和。
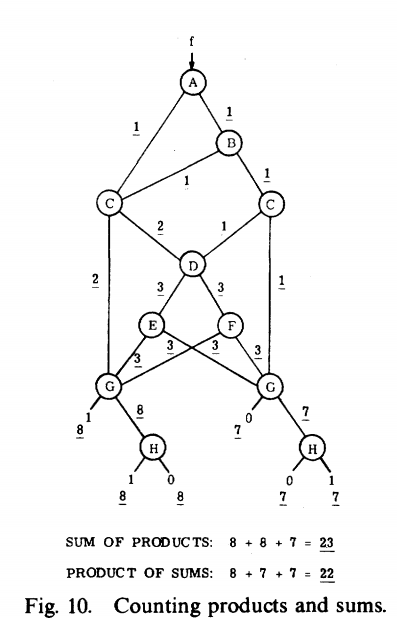
图的简化(reduce) (ODBB)
简化后的函数图包含以下性质:
- 不包含左右子节点相同的节点
- 不包含这样的节点:分别以左右子节点为根节点的子图同形
注:在简化的图中,以每一节点为根的子图也是简化的。任意的布尔函数有唯一的简化图可以将其表示,使得图的节点数目最少
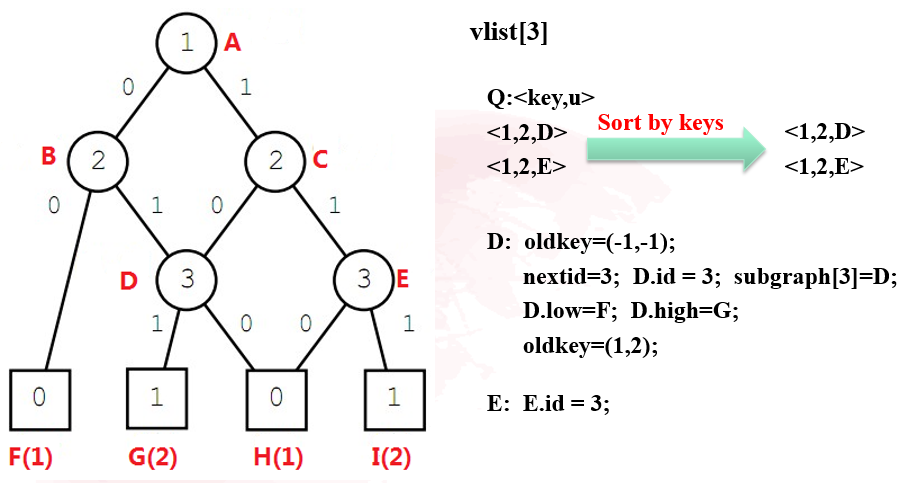
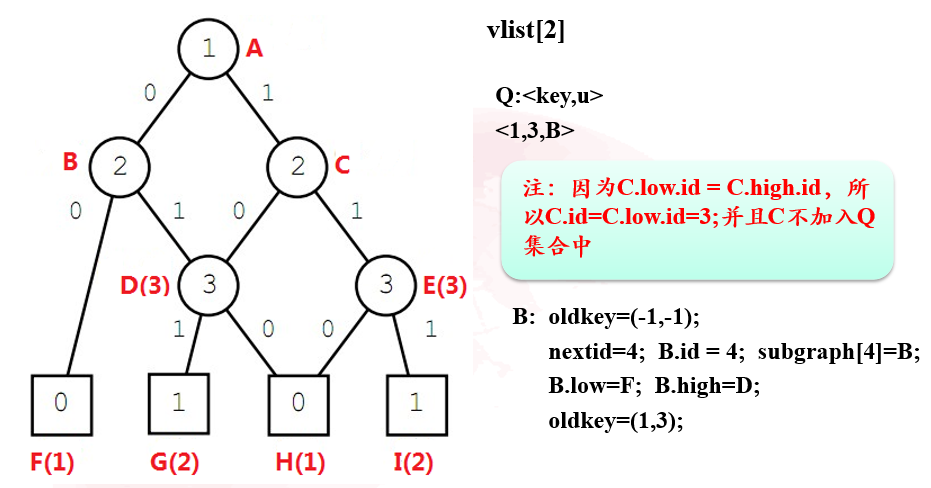
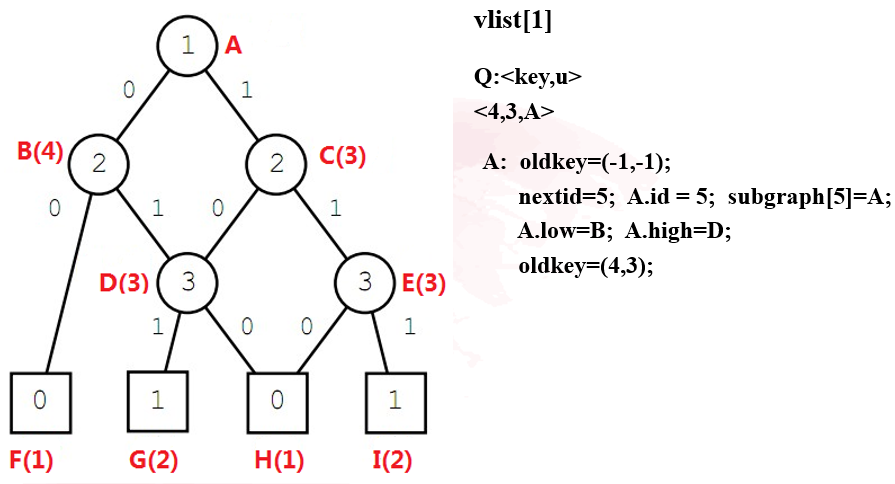
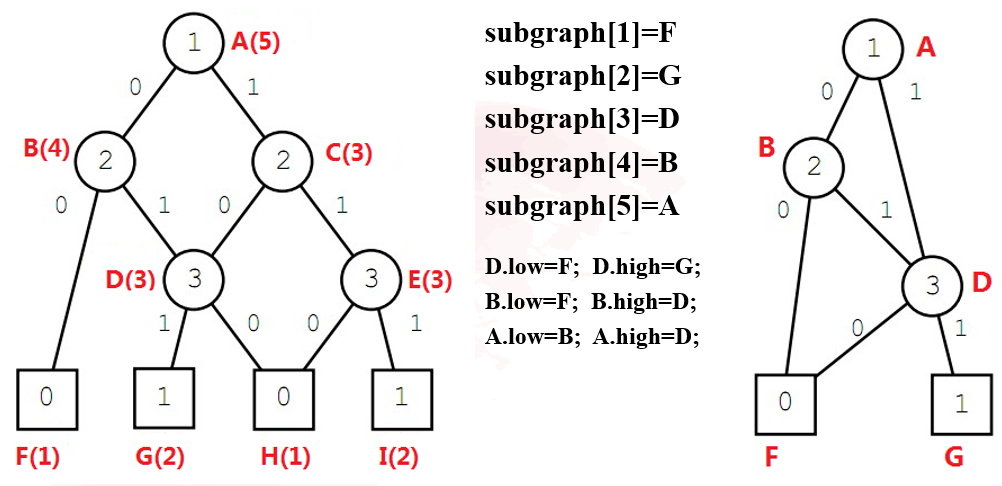
化简思想为:将原图按层排列,从终止节点(底层)依次向上进行标记,最后相同标记的只取一个节点就完成了图的简化。
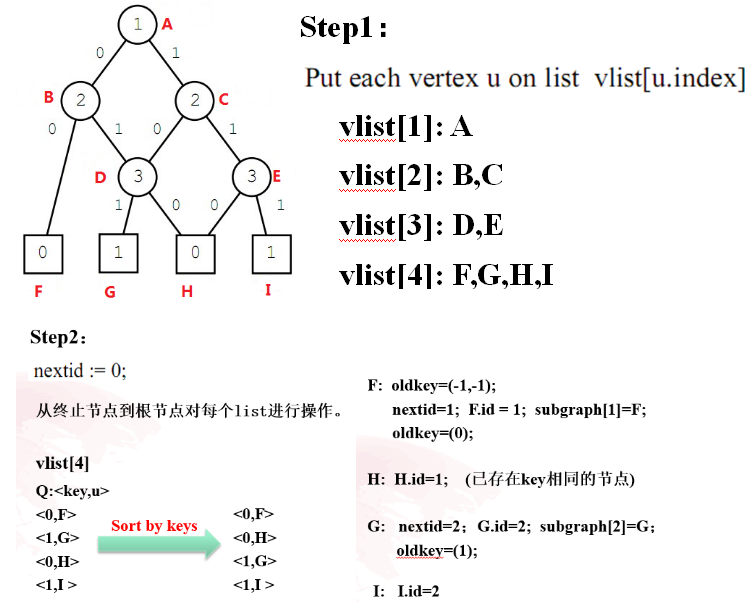
步骤:
- 将节点放到各层列表中,此处要注意的是,要把终止节点全部放在最后一层
- 从终止节点到根节点对每层的list进行操作:
- 对于每个节点,oldkey的初始化均为(-1,-1),终止节点的oldkey最后应该只有一个0或1值,同时终止节点最终也应该至多只有两个id(1,2)和oldkey(0,1)
- 对于非终止节点,其oldkey最后为两个值,前一个值表示其取0时应该指向的节点id,另一个值表示其取1时应该指向的节点id。low,high分别表示其取0和1时指向的节点。
- 当某个节点的low值和high值相等时,说明该节点的取值对于该分支的最终结果并没有影响,因此可以直接删除该节点。
OBDD的Apply操作
通过深度优先搜索的方法,对一些已知的布尔函数 OBDD 表示进行二元布尔运算得到另外一些布尔函数 OBDD 表示的操作。整个过程从上至下进行,我们需要做的预备工作是给每个节点编号(1,2,3.... 每个都不相同),然后从顶层开始,用两个 OBDD 树的顶层的节点合成一个新的节点,合成的规则就三种:
- 两个节点都为叶节点,可以直接根据布尔运算得出结果,合成的节点也是叶节点。
- 如果有一个节点为非叶子节点,看这两个节点的 index 值是否一样,如果是一样的,比如两个节点都表示 x1,那么新节 点的 index 就是 x1,新节点的左孩子通过两个老节点的左孩子生成,新节点的右节点通过两个老节点的右孩子生成。
- 如果两个节点的 index 值不同,比如 index(u)<index(v),新节点的 index 为较小的 index(u),新节点的左孩子由 u 的左孩子与 v 生成,新节点的右孩子由 u 的右孩子与 v 生成,当 index(u)>index(v)反过来做即可。
举例:
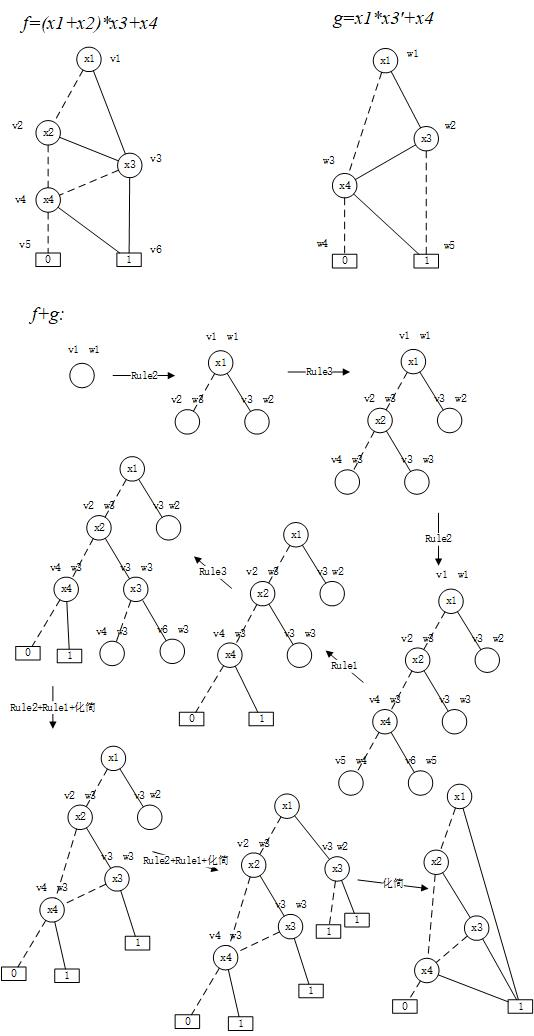
Reduce Function Graph(rfg)
定义:
一个fg称为是reduce的,如果它满足:1、没有一个节点的low,high节点相等;2,任意两个节点作为根节点所蕴含的子图不同构。
定理1
对于任何布尔函数f,都有表示f的唯一(直至同构)约简函数图,表示f的任何其他函数图都包含更多的顶点。
证明:
If={i|f|xi=0≠f|xi=1}
归纳奠基:
当|If|=0时,f必然是0或1,设G是表示函数0的rfg,易知此图中不包含1节点。
现在假设G至少包含一个非终端顶点,由于此图是无环图,则必然有:
一个非终节点的low/high节点均为终节点,又因为不包含1节点,则low/high节点都是0:
- 这个非终结点的low/high节点不同,此时,它们作为根节点所蕴含的子图同构
- 这个非终结点的low/high节点相同
上述情况均与G是rfg矛盾。
归纳假设:
假设定理1对于所有|Ig|<k的函数g成立,此时令|If|=k,其中k>0:
令i是If中值最小的元素,令f0=f|xi=0,f1=f|xi=1。f0和f1都有小于k的依赖集,因此用唯一的约简函数图表示(假设)。
设G和G‘是f的约简函数图,接下来证明这两个图同构,并可以用一个根节点和分别表示f0和f1的low/high子图表示。
设v和v‘是两个图中的非终节点,使得index(v)=index(v')=i。易知以v,v’为根节点的子图都表示f,因为f不依赖于index(v*)<i的任何节点v*。v,v‘的low节点所蕴含的子图都表示f0,因此,这两个子图可以通过某种映射sigma_0建立关系,同理,存在某种同构映射sigma_1链接high节点所蕴含的子图。
现声明,由v,v’为根节点的子图通过映射sigma链接:
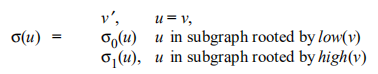
接下来证明sigma的定义是完备的,且sigma是同构映射。
函数性:
如果顶点u既包含在由low(v)为根的子图中,也包含在由high(v)为根的子图中,那么由sigma_0(u)和sigma_1(u)为根的子图必须与由u为根的子图同构,从而相互同构。由于G‘不包含同构子图,这只能在sigma_0(u)=sigma_1(u)时成立,因此上述sigma定义不存在冲突。
单射性:
如果G中有sigma(u1)=sigma(u2)的不同顶点u1和u2,则由这两个顶点为根的子图将与由sigma(u1)根的子图同构,从而导致G中包含两个由不同节点为根的子图同构,与G是rfg矛盾。
满射性:
由sigma_0,sigma_1均为满射,因此,根据定义,G’中所有的点在G中均存在原象。
同构:
综上,sigma是同构映射。
通过类似的推理,我们可以看到图G一定包含一个index(v)=i的顶点v,因为如果存在其他这样的顶点,则由它和v为根的子图将是同构的。
实际上v必然是根节点:假设有一些顶点u有index(u)=j<i,且没有其他顶点w有j<index(w)<i。由于函数f不依赖于xj,因此由low(u)和high(u)为根的子图都表示f,但这意味着low(u)=high(u)=v,这与G是rfg矛盾。
同理,由同构映射sigma,v‘为G’的根节点。
最后证明,rfg具有最少顶点数。现假设G不是rfg,然后我们可以构造一个较小的图表示G所表示的函数:
- 如果G包含一个low(v)=high(v)的节点v,那么消除这个节点,用low(v)代替它的位置
- 如果G包含两个节点v,v‘为根的子图是同构的,那么消除v’,v继承其所有子节点。
证毕!
布尔表达式因子次序与rfg的节点数
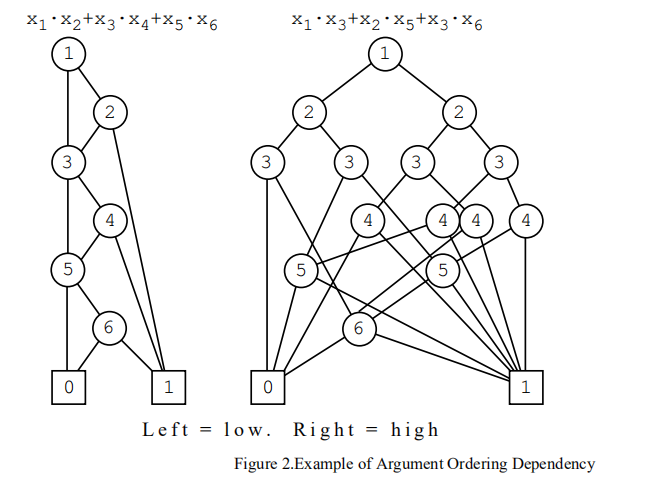
图中显示了参数的排序如何影响表示函数的图的大小的极端情况。输入排序的初始选择很差,可能会产生非常不利的影响。
DPLL
DPLL(Davis-Putnam-Logemann-Loveland)算法,是一种完备的、以回溯为基础的算法,用于解决在合取范式(CNF)中命题逻辑的布尔可满足性问题;也就是解决CNF-SAT问题。
SAT
给定一个命题公式,确定是否存在变量赋值以使该公式计算为真,这称为布尔可满足性问题。结果是,找到一个满足条件的解决方案或者证明不存在解决方案。
SAT问题的基本形式指给定一个命题变量集合X和一个X上的合取范式φ(X),判断是否存在一个真值赋值t(X),使得φ(X)为真。如果能找到,则称φ(x)是可满足的(satisfiable),否则称φ(x)是不可满足的(unsatisfiable)。SAT问题的模型发现形式指当φ(x)可满足时,给出使公式φ(x)可满足的一组赋值。
实际生产中的 NP 难题可以转化为 SAT 问题进行求解,因此,首先要进行规约和编码,目前 SAT 问题编码多采用 CNF 形式。DIMACS 作为标准格式广泛用于 CNF 布尔公式,也被历届 SAT 国际竞赛采用。
DIMACS文件用字符 c 引导的注释文字行开始。紧接注释之后的一行 p cnf 表示该实例是 CNF 形式的公式, nbvar 指公式包含的变量数目, nbclauses 指公式包含的子句数目,要求1至 nbvar 之间的每个变量至少在某个子句中出现一次。然后下面各行是子句序列,每个子句由一系列互不相同的介于 -nbvar 和 nbvar 的非空数字组成,并以 0 结束。正的数字表示相应序号变量的正文字形式,负的数字表示对应序号变量的负文字形式。
最近几年的SAT国际竞赛结果证明,预处理技术对SAT求解器性能至关重要。早期的预处理技术使用原始 DPLL (DavisPutnamLogemannLoveland,简称DPLL)提出的单元传播和纯文字规则,后来发展了一些更复杂的技术如超二元解析、单元子句和探针等。
命题逻辑基于SAT Solver的DPLL可满足性判定算法
合取范式样例:(p∨q∨r)∧(p∨┐q∨r)∧(┐p∨q∨r)
析取范式样例:(p∧q∧r)∨(p∧q∧┐r)∨(p∧┐q∧r)∨(┐p∧q∧r)∨(┐p∧┐q∧r)
DPLL 的核心思想就是依次对 CNF 实例的每个变量进行赋值,其搜索空间可以用一个二叉树来表示,树中的每个节点对应一个变量,取值只能为 0 或 1,左右子树分别表示变量取 0 或 1 的情况,从二叉树中根节点到叶子节点的一条路径就表示 CNF 实例中的一组变量赋值序列,DPLL 算法就是对这棵二叉树从根节点开始进行 DFS(深度优先搜索) 遍历所有的通路,以找到使问题可满足的解。
预处理:将公式转换为对应的合取范式(CNF)
DPLL框架
- Iterative Description(迭代描述)
status = preprocess(); //预操作 if (status!=UNKNOWN) return status; while(1) { decide_next_branch(); //变量决策环节 while (true) { status = deduce(); //推理环节(BCP) if (status == CONFLICT) { blevel = analyze_conflict(); //冲突分析 if (blevel == 0) return UNSATISFIABLE; else backtrack(blevel); //智能回溯,对应 }else if (status == SATISFIABLE) return SATISFIABLE; else break; } }
- Recursive description(递归描述)
DPLL(formula, assignment){ necessary = deduction(formula, assignment); new_asgnmnt = union(necessary, assignment); if (is_satisfied(formula, new_asgnmnt)) return SATISFIABLE; else if (is_conflicting(formula, new_asgnmnt)) return CONFLICT; var = choose_free_variable(formula, new_asgnmnt); asgn1 = union(new_asgnmnt, assign(var, 1)); if (DPLL(formula, asgn1)==SATISFIABLE) return SATISFIABLE; else { asgn2 = union (new_asgnmnt, assign(var, 0)); return DPLL(formula, asgn2); } }
基于迭代的实现相对于基于递归的实现有以下优势:
- 递归速度慢且容易发生溢出,相对于迭代就有很多自身的劣势。
- 迭代具有非时间顺序回溯(智能回溯)的优势。
- 递归需要更多的内存存储空间。
DPLL算法框图
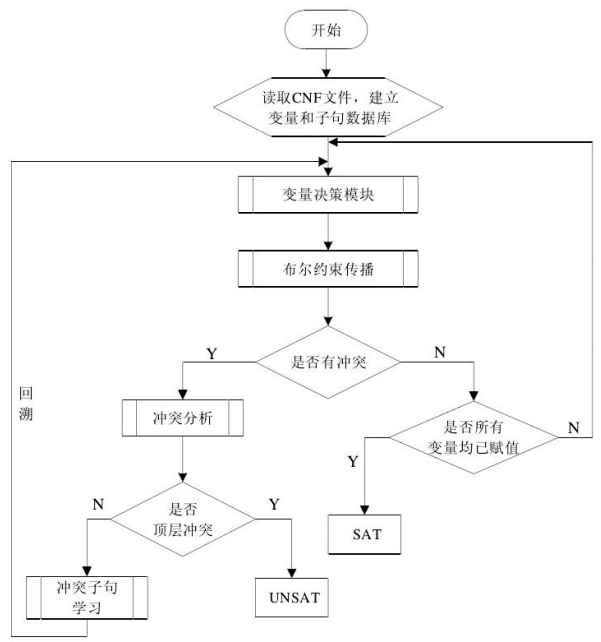
算法流程
- preprocess()预处理操作,其实就是对 CNF 实例进行各种化简减轻后续的求解工作量。
- 如果预处理不能直接 得出结果的话,就进行后面的 decide_next_branch()操作,这就是变量决策操作,它会分析从 哪个变量开始赋值是最合适的。
- 对变量赋值以后,会执行一个deduce() 操作,可以管它叫推理操作,目的是识别该赋值所导致的必要赋值。
- 当然不正确的赋值可能会产生错误,这就会产生冲突,我们需要 analyze_conflict()分析这个冲突得到冲突发生的根源位置
- 通过 backtrack()回溯到这个位置,为这个变量赋另外一个值
- 继续往下搜索,如此循环,直到找到满足 SAT 的一组真值指派
- 如果回溯到了最顶层还没有解 决问题的话,那就表示这个 CNF 实例是不可满足的
变量决策(decide_next_branch())
基于这样的一个事实:先对哪个变量进行赋值,会直接影响二叉搜索树的规模大 小,也就会影响求解时间,所以如何快速有效地决策出下一个将要赋值的变量,这很重要。以下将介绍三种变量决策方式:
- MOM(JW)方法
在一个子句中, 只要一个文字得到满足,那么这个子句就得到满足了。
所以,如果一个子句的长度越长(含有字母数越多),那么可以使得该子句满足的文字数目也就越多,这个子句也就越容易满足,所以它就不是所谓的“矛盾的主要方面”,我们不需要过于关注这个子句;然而,如果一个子句长度很小,那它就很不容易被满足,所以我们要优先考虑它们,给予它们更高的权重, 这样做的目的就是让那些不容易被满足的子句优先得到满足。
具体的方法是求解出和变量 ll相对应的 JJ值,哪个变量 J 值大就选哪个先赋值,变量对应的 JJ值的计算公式如下:
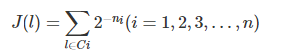
其中 l 表示变量,Ci表示包含变量 i 的子句,共有 m 个子句, ni 表示这个子句的长度。它体现出了 MOM 算法的两个关键点:“最短的子句”和“出现频率最高的变量”,”最短子句”体现在长度越短(n 越小), 2^{−ni}的值就越大,它能给J 值的贡献就越多;”出现频率最高的变量”体现在 l 出现次数越多的话,相加的项数就越多,J 值就更容易变的很大。
- Literal Count Heuristics 方法
它主要是统计已经给某些字母赋值但仍然没有得到满足的子句的数量,这个数量依赖于变量赋值,所以每次换变量的时候,所有自由变量都需要重 新统计这个数量,效率较低。
- VSIDS,Variable State Independent Decaying Sum(独立变量状态 衰减和策略)
- 为每一个变量设定一个 score,这个 score 的初始值就是该变量在所有子句集中出现的次数
- 每当一个包含该字母的冲突子句被添加进数据库,该字母的 score 就会加 1
- 哪个变量的 socre 值最大,就从这个变量开始赋值
* 另外,为了防止一些变量长时间得不到赋值,经过一定时间的决策后,每一个变量的 score 值都会被 decay,具体方式是把 score 值除以一个常数(通常为 2-4 左右)
推理(deduce())
当一个变量被赋值后,可以通过推理来减少一些不必要的搜索,加快效率。推理过程主要依赖于 Unit clause rule(单元子句规则)。
所谓单元子句就是:
在这个子句中,除了一个文字未赋值外,其他所有的文字都被赋值并体现为假,这样的子句就是 Unit clause(单元子句),剩下的 这个文字就是 unit literal(单元文字)。
很容易知道,在单元子句中,这最后一个文字必须体现 为真,整个子句才能被满足,把所有的单元文字都赋值并体现为真的过程就是 BCP(布尔约束传播)。
BCP 的目标就是识别出单元子句并对单元文字赋值,能够减少搜索空间或提前逼出冲突。
以下将介绍三种BCP实现方法:
- counters 方法
具体做法是是为每个变量设置两个 lists,分别用来保存所有包含这个变量的正负字母的子句,并且每个子句都设置两个计数器,分别统计体现为真的字母数和体现为假的字母数。如果体现为假的字母等于总字母数,那就产生了冲突;如果体现为假的字母数比总字母数少 1,那就出现了单元子句,就需要对单元文字进行自动赋值。举例:
1:(┐m∨n∨p)
2:(m∨p∨q)
3:(m∨p∨┐q)
4:(m∨┐p∨q)
5:(m∨┐p∨┐q)
6:(┐n∨┐p∨q)
7:(┐m∨n∨┐p)
8:(┐m∨┐n∨p)
计算过程:
- 初始的时候,1-8 号子句各有两个计数器(分别记录赋值为 0 和 1 的文字数量),一开始所有计数器的值都是 0
- 变量 m 有链表分别用来保存所有包含 m 和 ┐m 的子句,包含 m 的 链表中有子句 2,3,4,5,而包含 ┐m 的链表中有子句 1,7,8,其余变量也均有这样的两个链表。
- 当给 m 赋 0 时,包含 m 的链表中的子句 2,3,4,5 的 0 计数器就会更新,数量加 1, 包含 ┐m 的链表中的子句 1,7,8 的 1 计数器也会更新,数量加 1
- 如果再给 p 赋 0 的话,包 含 p 的链表中的子句 1,2,3,8 的 0 计数器就也会更新,数量加 1,此时 2,3 两个子句的 0 计数器数量变为 2,比总文字数 3 少 1,均成为了单元子句
- 2 可以推出 q 必须赋 1,而 3 可以 推出 q 必须赋 0,产生冲突,BCP 完成任务
- head/tail list 方法
它为每个子句设置两个引用指针,分别是头指针和尾指针,初始时,头指针指向子句第一个文字,尾指针指向最后一个文字,每个子句的文字存放在一个数组中。
对于一个变量 v,设置有四个链表,分别装有句头是 v 的子句,句头是非 v 子句,句尾是 v 的子句, 句尾是非 v 的子句,分别标记为 clause_of_pos_head(v),clause_of_pos_tail(v), clause_of_neg_head(v),clause_of_neg_tail(v)。
假设有 m 个子句的话,所有变量的四个链表中就共存放着 2m 个子句,无论后面这些子句怎么调换位置,子句总数是不变的。
假设某变量 v 被赋值为 1,那么所有句头和句尾为 v 的子句就都可以忽略了,因为他们已经被满足了。而对于句头或句尾是非 v 的子句,就需要移动头尾指针寻找下一个未被赋值的字母,头指针往后移,尾指针往前移,移动时可能会发生以下四种情况:
- 第一个遇到的文字 l 已经体现为真了,那么子句就已经满足了,什么都不用做,忽略这个子句就行了。
- 第一个遇到的文字 l 是未赋值的,且不是句尾,那么就把这个子句 c 从 v 的链表中移除,放入到 l 的对应的链表中。
- 如果头尾之间只剩一个变量未赋值,其他文字都体现为假了,就出现了单元子句,直接推断出单元文字的取值。
- 如果头尾之间所有文字都体现为假,那产生冲突,需要回溯。当一个变量被赋值的时候,平均有 m/n 个子句需要更新(m 为子句数,n 为变量数)。
举例:
1:(┐m∨n∨p)
2:(m∨p∨q)
3:(m∨p∨┐q)
4:(m∨┐p∨q)
5:(m∨┐p∨┐q)
6:(┐n∨┐p∨q)
7:(┐m∨n∨┐p)
8:(┐m∨┐n∨p)
初始时,我们可以将各个子句填入变量的链表中,如下表所示:
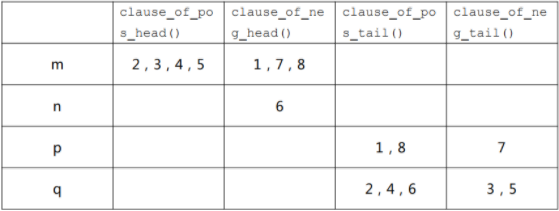
此时,头尾指针分别指向每个子句的头部和尾部。
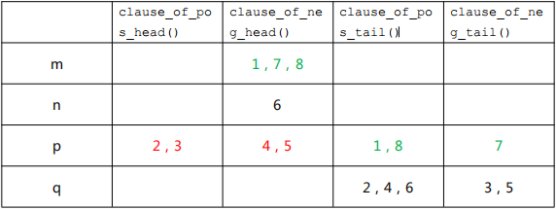
当我们给 m 赋值为 0 的时候,m 的 clause_of_neg_head(m)链表中的子句 1,7,8 就可以忽略不看了,因为已经被满足,把它们标注为绿色,
而 clause_of_pos_head(m) 中的子句 2,3,4,5 还没有被满足,这些子句头指针需要后移一位,转移后这些子句的头指针指向的文字就不是 m 了,所以需要将表格中 2,3,4,5 的位置换一下,更换位置的子句用红色标注,这次赋值后结果如下:
以此类推,当我们再给 p 赋 0 的时候,4,5 就可以不用考虑了,2,3 的头指针需再后移一位,2,3 在表格中的位置也需要更换,如下表所示:
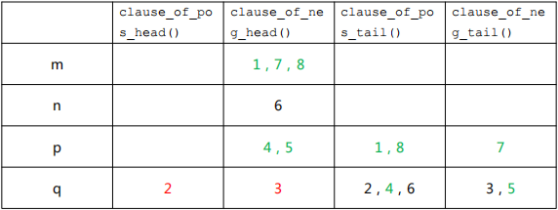
此时已经满足条件(3,头尾指针重叠)了,形成了两个单元子句,2 可以推出 q 必须赋 1,而 3 可以推 出 q 必须赋 0,产生冲突,BCP 完成任务。
- 2-literal watching
这个方法与 H/T 类似,也要为每个子句关联两个指针,与 H/T 不同之处是,这两个指针没有先后次序,也就没有所谓的头和尾的概念,这样设置会带来很多好 处,比如初始时这两个指针的位置可以是任意的(H/T 必须放在头和尾的位置),移动时也可 以向前后两个方向移动(H/T 中头指针只能向后移,尾指针只能向前移),回溯时无需改动指针的位置(H/T 回溯时需要把指针变回原来的位置)。但这种设置也有弊端,即只有遍历完所 有子句的文字后,才能识别出单元子句。相对应的,每个变量 v 也设置了两个 list 来分别存放以 watching 指针分为 v 以及非 v 的子句。接下来的操作都与 H/T 类似,当某个变量 v 赋值为 1 的话,watching 指针为 v 的子句可以忽略,watching 指针为非 v 的子句开始移动指针。
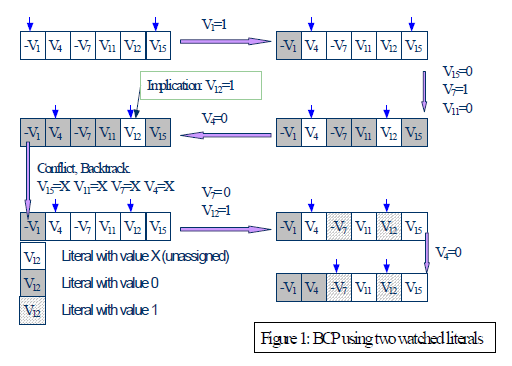
冲突分析与学习(analyze_conflict())
目的是找到冲突产生的原因,这就是分析的过程;并告诉 SAT 处 理器这些搜索空间是会产生冲突的,以后不要再踩这些坑了,这就是学习的过程。
早期解决冲突的方法就是回到上一层,将变量取值翻转,继续往下进行搜索,这也叫时序回 溯。但是这样做的结果很可能是冲突依旧存在,因为上一层的赋值也许并不是冲突产生的根本原 因,从而白白浪费一次计算的时间,效率非常低。目前主流的 SAT 处理器都采用基于冲突分析和学习的非时序回溯算法,它可以智能地分析 出冲突产生的根本原因,并回跳多个决策层,并把会导致冲突的子句加入到子句集中。
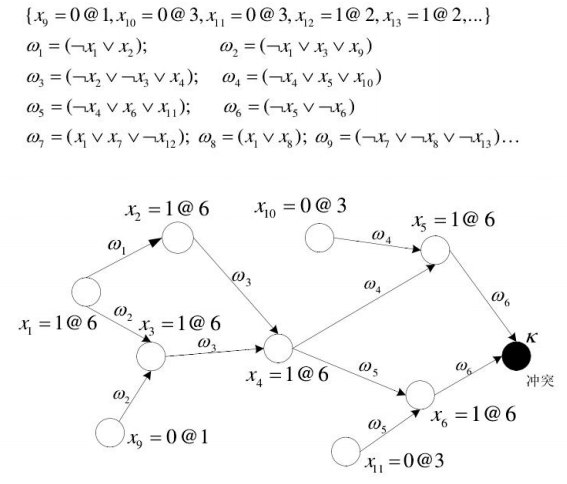
从图中我们可以看出,导致冲突产生的根本原因是第 1 层中将 x9 赋为 0,在第 3 层中 将 x10 赋为 0,在第 3 层中将 x11 赋为 0,在第 6 层中将 x1 赋为 1(x1=1@6 表示在第 6 层将 x1 赋值为 1)。
由此我们可以直接回溯到第 3 层进行重新赋值,而不是仅仅回溯到上一层,并且我们知道(x_9 = 0) \cup (x_{10} = 0) \cup (x_{11} = 0) \cup (x_1 = 1) 会导致冲突,我们就可以添加子句会导致冲突,我们就可以添加子句w_{10} = (x_9 \cup x_{10} \cup x_{11} \cup !x_1) 添加进子句库中,在接下里的搜索过程中就能预防相同的变量赋值再次出现。
analyze_conflict(){ cl = find_conflicting_clause(); // 找到冲突子句 cl while (!stop_criterion_met(cl)) { lit = choose_literal(cl); // 选择一个文字 var = variable_of_literal( lit ); //这个文字所对应的变量命名为var ante = antecedent( var ); // ante 为一个单元子句 cl = resolve(cl, ante, var); // resolve()返回一个子句,除了 var 所对应的文字,这子句需要包含 cl 和 ante 中的 // 所有文字,其中 cl 是一个冲突子句,ante 是一个单元子句,所以返回的 cl 也是一个冲突子句 } add_clause_to_database(cl); back_dl = clause_asserting_level(cl); return back_dl; }
数据的储存
数据存储方式主要包括以下三种:
- 早期的链表和指针数组的存储方式
- 数组方式
- trie 存储方式
各个方法优缺点:
数组方式:数组采用连续空间存储,内存利用率和存储效率更高,局部访问能力更强。连续存储能提高,cache 命中率,从而增加计算速度。但不灵活。
链表方式:便于对子句进行增加和删除操作,存储效率低。因为缺少局部访问能力,往往会造成缓存丢失。
head/tail 和 2-literal watching 都被称为“膨胀数据结构”,它们都采用数组存储子句,最具竞争力。
以下主要介绍Tire数据存储方式。
Tire 是以三叉树的方式存储,它的每个内部节点都是都是一个变量的索引,从根节点到叶节点路径上的所有变量组成一个子句。每个节点的三条孩子边分别被标记为 Pos(positive)、Neg(negative)和 DC(dont care),例如节点 v 的 Pos 边表示文字 v,Neg 边表示文字 !v ,DC 边表示没有这个变量的文字。Tire 的叶节点是 T 或者 F,T 表示 CNF 实例中有这个子句,F 表示没有这个子句。下面是文中给出的一个例子:
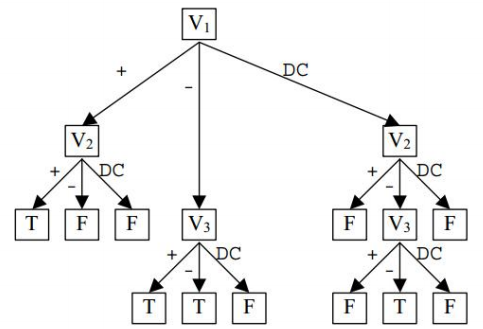
从图中我们可以清楚地看出这个 CNF 实例中有哪些子句。
zchaff代码(尝试)理解
zchaff_base.h
class CLitPoolElement { protected: int32 _val; public: // constructors & destructors CLitPoolElement(void):_val(0) {} ~CLitPoolElement() {} // member access function int & val(void) { return _val; } // stands for signed variable, i.e. 2*var_idx + sign int s_var(void) { return _val >> 2; } unsigned var_index(void) { return _val >> 3; } unsigned var_sign(void) { return ((_val >> 2) & 0x1); } void set(int s_var) { _val = (s_var << 2); } void set(int vid, int sign) { _val = (((vid << 1) + sign) << 2); } // followings are for manipulate watched literals int direction(void) { return ((_val & 0x3) - 2); } bool is_watched(void) { return ((_val & 0x3) != 0); } void unwatch(void) { _val = _val & (~0x3); } void set_watch(int dir) { _val = _val + dir + 2; } // following are used for spacing (e.g. indicate clause's end) bool is_literal(void) { return _val > 0; } void set_clause_index(int cl_idx) { _val = - cl_idx; } ClauseIdx get_clause_index(void) { assert(_val <= 0); return -_val; } // misc functions unsigned find_clause_index(void) { CLitPoolElement * ptr; for (ptr = this; ptr->is_literal(); ++ptr); return ptr->get_clause_index(); } // every class should have a dump function and a self check function void dump(ostream & os= cout); friend ostream & operator << (ostream & os, CLitPoolElement & l) { l.dump(os); return os; } };
class CLitPoolElement :定义一个名为CLitPoolElement的类(作用类似struct,但默认成员访问权限为private)。
protected :半公开成员。protected与private基本相似,只有在继承时有较大的区别。继承的类可以访问protected成员,但是不能访问private成员。
CLitPoolElement(void):_val(0) {} 构造函数 & 析构函数。构造函数用于初始化_val变量值为0。
~CLitPoolElement() {} 析构函数有助于在跳出程序(比如关闭文件、释放内存等)前释放资源。
val() :返回_val
s_var() :_val除4
var_index() :_val除8
var_sign() :右移2位,保留末位
set(s_var) :s_var乘2
set(vid, sign) :vid乘2加sign,整体乘4
操作观察文字:
direction() :_val保留2进制最后两位,减2,结果为1,0,-1
is_watched() :_val保留2进制最后两位,判断是否等于0,结果为1,0
unwatch() :将_val最后两位置0
set_watch(dir) :将_val+dir+2
用于间距(例如,指示子句的结尾):
is_literal() :判断_val的值是否大于0
set_clause_index(cl_idx) :将-cl_idx的值赋给 _val
get_clause_index() :返回-_val,如果_val本身小于0,则不做操作
其他:
find_clause_index() :找到第一个不是literal的词
每个类都应该有一个dump函数和一个自检函数。
一些例题:
- 子句(Clause)数据结构设计
1、设计一个基于数组的数据结构存储子句数据(clause data)中的文字、子句与公式。
用数组存储子句的文字,对于每个数组设置两个指针,分别为头指针与尾指针,然后对于每个变量v设置4个指针,分别装有句头是 v 的子句,句头是非 v 子句, 句尾是 v 的子句,句尾是非 v 的子句,这样存储的子句,无论子句顺序及其中变量顺序的改变都不会影响所有变量的四个链表中的子句数量。取所有变量v是句头的子句与非v是句头的子句或者v是句尾的子句与非v是句尾的子句合取可以得到公式。
2、列举出相比于指针(pointer-heavy)数据结构,用数组存储子句的优点
数组采用连续内存空间存储,内存利用率更高,访问局部变量速度更快;
对于cache命中而言,由于数组在内存上连续存储,相比于链表的不连续存储能够提高cache命中率,从而能够增加计算速度。
- 简述为什么在DPLL算法的实现中往往采用迭代实现而不是递归实现。
递归速度慢且容易发生溢出,相对于迭代就有很多自身的劣势;
迭代具有非时间顺序回溯(智能回溯)的优势。
- 基于计数器的BCP算法是一种容易理解与实现的 BCP 算法。假设每个子句(clause)拥有两个计数器(counter),一个用于子句中的值1字面量(literal)的计数,一个用于子句中的值0字面量的计数。每个变量(variable)都有两个列表,其中包含所有子句,其中该变量分别显示为正值和负值。当为变量分配一个值时,包含此字面量的所有子句将更新其计数器。设实例具有m个子句(clause)和n个变量(variable),并且平均每个子句具有l个字面值(literal)。那么每当给一个变量赋值时,有多少个计数器(counter)需要更新。简要概述分析过程。
l/n表示每个变量平均在每个子句中出现的次数,然后乘以子句的数量m,所以,有一个变量被赋值的时候,会有平均 ml/n 个计数器需要更新,在回溯的时候,每取消一个变量赋值,也会平均有 ml/n 个计数器的更新。
- Judge if there are conflicting clauses in the following CNFs. If not, write all feasible assignments.
(x∨y∨z)(x∨┐y)(y∨┐z)(z∨┐x)(┐x∨┐y∨┐z)
假设x=0,(x∨┐y)=>y=0+(y∨┐z)=>z=0
x=0,y=0,z=0=>(x∨y∨z)=0
假设x=1,(z∨┐x)=>z=1+(y∨┐z)=>y=1
x=1,y=1,z=1,=>0
所以说,所有的值都使得这个语句结果为0,根据定义,是冲突语句(*就是deduce的过程)。
FDS
一个Fair Discrete System,D=<V,O,\Theta,p,J,C>包括:
- V:一个有限的类型化状态变量,一个V-state s表示V的一个解释
\sum_V:表示所有的V-states集合
- O \subseteq V:可观察变量的集合
- \Thata:一个初始条件。一个描述初始状态的能够满足的断言。
- \rho:一个过渡关系。一个断言\rho(V,V'),引用状态变量的当前版本和即将变换成的版本。例如:x'=x+1对应于赋值,x:=x+1
- J=J_1,...,J_k:一个公平的(justice)需求集合。确保对于每个j_i,i=1,...,k的计算包含无线多个j_i-states。
- C={<p_1,q_1>,...,<p_n,q_n>}:一个包含compassion需求的集合。无限多个p_i-states意味着无限爱多个q_i-states。
例子:

- 首先表示V,状态变量
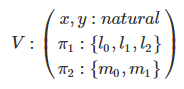
- 首先第一行就是程序最上面的初始化,左边两个变量,右边 natural。
- 接下来定义\pi ,程序有几个部分(用||连接)就定义几个 ,每个\pi 对应的元素就是每一行语句l_0 ~l_k
- 表示\Theta
![]()
\Theta表示初始条件,而初始时,每个\pi都处于第一行语句l_0,再加上变量的初始化,把它们合取。
- 表示\rho:
定义:
- \pi'在此表示下一个状态
- pres(V)。对于V里面的每个元素都可以这样表示:e=e',然后把它们用合取符号连接起来。上面例子的pres(V)就应该表示为:
pres(V) : \pi_1'=\pi_1∧\pi_2'=\pi_2∧x'=x∧y'=y
- at_l_i是一个缩写,表示\pi_i=l_j,at'_l_j表示\pi_i'=l_j
- \rho_I=pres(V),\rho_{l_0}表示语句l_0转换成逻辑公式之后的一个符号。
\rho:\rho_I∨\rho_{l_0}∨\rho_{l_1}∨\rho_{m_0}
语句的表示
- 赋值语句
y:=e
进行该语句时,需要进行以下状态检查以确定该赋值语句是否能够成立。
at_l_i∧at'_l_k∧y'=e∧pres(V-{\pi_i,y})
则对于上述案例:
\rho_{m_0} : \pi_2=m_0∧\pi_2'=m_1∧\pi_1'=\pi_1∧x'=1∧y'=y
- if语句:if b then l_1 : S_1 else l_2 : S_2
如果没有else,那么l_2就是跳出if下一步要执行的语句
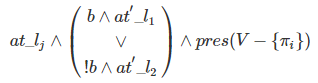
- while语句:while b do l_1 : S_1
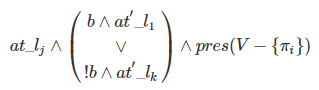
则对于上述案例:(是\rho_{l_0},不是p_{l_0})
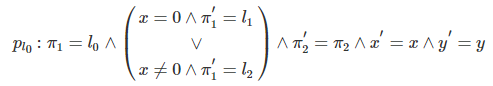
- 表示J:J表示单个的若公平性,还有就是只要某语句想执行,那这语句就可以一直执行,然而在这个程序中,我们发现,如果让p1一直执行,而不执行p2,那么这个程序将y将一直循环下去,这无疑不是我们想要的所以我们要加限定条件了也就是J这个正义集合:一般把┐at_l_j这个符号加入J集合中:
J : {┐at_l_0, ┐at_l_1, ┐at_m_0}
- 表示C:一般该集合为空集。
一些例题
- 将下列程序转换成逻辑公式
Program:
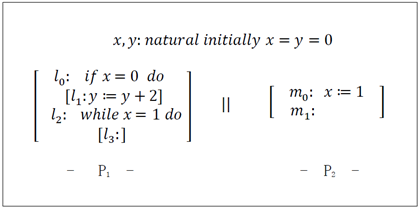
State variables: V
Initial condition: \Theta
Transition relation: \rho
Write the disjoints \rho_{l_0} and \rho_{m_0}

Alloy
Alloy搜索的方法是:给定一个定义域范围,对这个范围里所有的定义值都进行检查。本质是找语句中为假的可能,证明命题为假,因为为假说明命题一定错。
基础语法
sig :类似于class
pred :用于定义谓词
举例:
sig Platform {} // there are "Platform" things sig Man{ceiling, floor: platform} // each Man has a ceiling and a floor Platform pred Above(m, n: Man){ m.floor = n.ceiling } // Man m is "above" Man n if m's floor is n's ceiling
其中 m,n:Man 表示 m,n 都是 Man 的实例
fact :用来定义已知条件
举例:
fact { all m: Man | some n: Man | Above (n, m) } // one Man's ceiling is another Man's floor
该示例表示对于任意人来说,都存在某个人在他上面
assert :表示假设
check :用于检验
assert BelowToo{ all m: Man | some n: Man | Above(m, n) } // one Man's floor is another Man's ceiling ? check BelowToo for 2 // check "one Man's floor is another MAn's ceiling" // counterexample(反例) with 2 or less platform and men?
for 2 :表示范围,用于举例的实例个数。这里表示有2个Man和两个platform。我们的目标是找出不满足BelowToo的反例来证明该命题是错误的。这里一共有2^4种可能,首先第一步,我们就要排除掉不满足fact的,因为fact是已知条件,如果不满足fact,则不考虑。然后再在剩下的结果中找出不满足假设的,若找到,则证明假设有错误。
找出的一个反例如下:
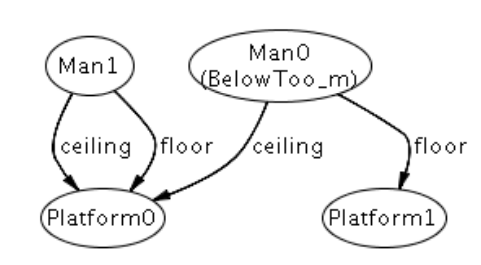
从此可以看出对于Man1,Man0在他的下面,但对于Man0来说,没有人在他下面,所以这种情况就不满足假设。
注:当举例时要注意考虑所有情况,而不是自己假设存在的合理情况,比如这里,Man1就在自己的上面,但是它依旧符合fact
abstract :定义抽象
all x: e | F // all: F holds for every x in e all x: e1, y: e2 | F all x, y: e | F all disj x, y: e | F
some :F holds for at least one x in e
no :F holds for no x in e
one :F holds for exactly one x in e
lone :F holds for at most one x in e
set :any number
disj :short of distinct
举例:
some n: Name, a: Address | a in n.address // some name maps to some address — address book not empty no n: Name | n in n.^address // no name can be reached by lookups from itself — address book acyclic all n: Name | lone a: Address | a in n.address // every name maps to at most one address — address book is functional all n: Name | no disj a, a': Address | (a + a') in n.address // no name maps to two or more distinct addresses — same as above RecentlyUsed: set Name // RecentlyUsed is a subset of the set Name
^ :表示传递闭包
+ :表示并集
- :表示差集
in :表示子集
. :表示点乘,和数据库中的left join相同,但是结果中会去掉相同的那一项
#r :r中的元组数
& :intersection,交集
= :表示判等
-> :交叉商,笛卡尔乘积
[] :相当于按key取值
~ :转置
* :自反传递闭包
举例:
{(N0)} + {(N1)} = {(N0), (N1)}
{(N0)} = {(N1)} = false
{(N0)} in none = false
{N0}.{N0, N1} = {N1}
{(N1), (N2)} & {(N0), (N2)} = {(N2)}
{(N0, A0), (N1, A1)} & {(N0, A0), (N1, A2)} = {(N0, A0)}
{(N0), (N1)} -> {(A0), (A1)} = {(N0, A0), (N0, A1), (N1, A0), (N1, A1)}
e1[e2] = e2.e1
a.b.c[d] = d.(a.b.c)
{(N0, A0), (N1, A0), (N2, A2)}[{(N1)}] = {(A0)}
~{(N0, N1), (N1, N2), (N2, N3)} = {(N1, N0), (N2, N1), (N3, N2)}
^{(N0, N1), (N1, N2), (N2, N3)} = {(N0, N1), (N0, N2), (N0, N3), (N1, N2), (N1, N3), (N2, N3)}
*{(N0, N1), (N1, N2), (N2, N3)} = {(N0, N0), (N0, N1), (N0, N2), (N0, N3), (N1, N1),
(N1, N2), (N1, N3), (N2, N2), (N2, N3), (N3, N3)}
<:: 域约束,后面集合中元组前面的一个值在前面指定的集合中
:>: 范围约束,第一个集合中元组后面的值在在后面指定的集合中
++: 相当于继承+重载
举例:
p ++ q = p – (domain(q) <: p) + q {(N0, N1), (N1, N2), (N2, A0)} :> {(A0)} = {(N2, A0)} {(N0, N1), (N1, N2), (N2, A0)} :> {(N0), (N1), (N2)} = {(N0, N1), (N1, N2)} {(N0), (N1)} <: {(N0, N1), (N1, N2), (N2, A0)} = {(N0, N1), (N1, N2)} {(N0, N1), (N1, N2), (N2, A0)} ++ {(N0, N1), (N1, A0)} = {(N0, N1), (N1, A0), (N2, A0)}
let: 定义局部变量
if f then e1 else e2: if语句
举例:
all n: Name | some n.workAddress => n.address = n.workAddress else n.address = n.homeAddress all n: Name | let w = n.workAddress, a = n.address | some w => a = w else a = n.homeAddress all n: Name | let w = n.workAddress | n.address = if some w then w else n.homeAddress all n: Name | n.address = let w = n.workAddress | if some w then w else n.homeAddress
一些例题
- “天花板与地板”模型(the Alloy Analyzer)
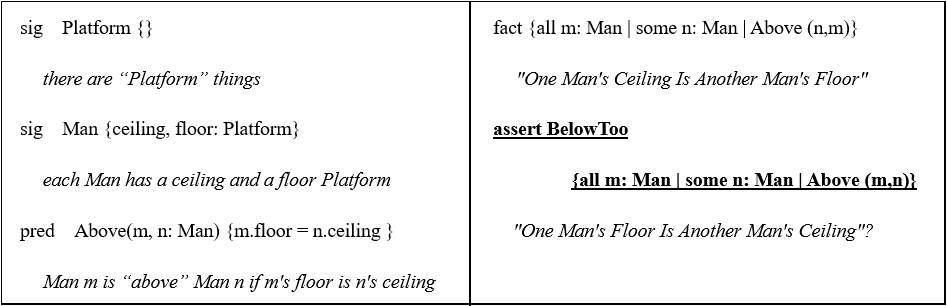
现在假设有2个Platform实例,2个 Man 实例,找出至少一个不满足断言“BelowToo”的反例,并用图形表示。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号